结巴分词原理

Posted 2021-11-23 一只小菜狗:D

文章目录

• 结巴分词简介
• 分词
• • 基于前缀词典实现高效的词图扫描，生成句子中汉字所有可能成词情况所构成的有向无环图
  • • 构造前缀词典
    • 构造有向无环图
  • 动态规划查找最大概率路径, 找出基于词频的最大切分组合
  • HMM识别未登陆词
• 关键词提取
• • TF-IDF
  • TextRank
• 词性标注
• 参考

在我的上一篇博客 概率图模型中，有介绍一些常见的概率图模型。而在日常工作中，结巴分词也是常用的中文分词包，且其中使用了HMM模型，结合 概率图模型中的理论知识，可以帮助我们进一步了解HMM算法（当然不仅限于此）。

结巴分词简介

首先，我们通过readme看看结巴分词能够做什么：

分词：
官方给出了使用的分词算法：

关键词抽取:


词性标注：

接下来，我们分三个小节分别介绍他们。

分词

为了能够更好的理解，用一个实例举例：

去北京大学玩

基于前缀词典实现高效的词图扫描，生成句子中汉字所有可能成词情况所构成的有向无环图

构造前缀词典

我们知道，结巴分词含有自带的词典，也可以支持用户自己添加词典。利用该词典构造前缀词典，该前缀词典被用于构造DAG。词典的形式如下：

词典格式和 dict.txt 一样，一个词占一行；每一行分三部分：词语、词频（可省略）、词性（可省略），用空格隔开，顺序不可颠倒。

根据词典，我们可以构造前缀词典，对示例“去北京大学玩”，其前缀词典的形式如下：

北京大学 2053
北京大 0 # 不存在前缀词，词频为0
北京 34488
北 17860
京 6583
大学 20025
大 144099
学 17482
去 123402
玩 4207

源码如下：

# f是离线统计的词典文件句柄
def gen_pfdict(self, f):
    # 初始化前缀词典
    lfreq = {}
    ltotal = 0
    f_name = resolve_filename(f)
    for lineno, line in enumerate(f, 1):
        try:
            # 解析离线词典文本文件
            line = line.strip().decode('utf-8')
            # 词和对应的词频
            word, freq = line.split(' ')[:2]
            freq = int(freq)
            lfreq[word] = freq
            ltotal += freq
            # 获取该词所有的前缀词
            for ch in xrange(len(word)):
                wfrag = word[:ch + 1]
                # 如果某前缀词不在前缀词典中，则将对应词频设置为0
                if wfrag not in lfreq:
                    lfreq[wfrag] = 0
        except ValueError:
            raise ValueError(
                'invalid dictionary entry in %s at Line %s: %s' % (f_name, lineno, line))
    f.close()
    return lfreq, ltotal

构造有向无环图

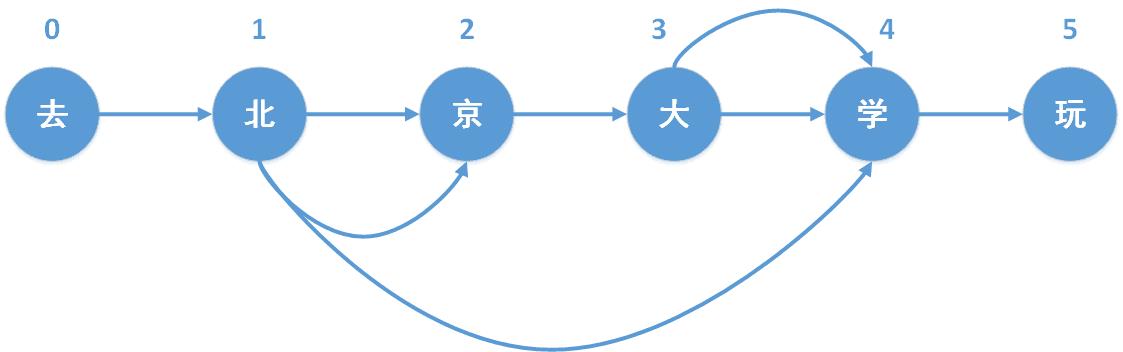
对jieba分词中，每个字都以其在句子中的位置去标记。其最终会生成一个dict，key代表每个词的开头，value代表着每个词的结尾（可能有多个）。对示例“去北京大学玩”而言，其DAG结果如下：

{
0: [0] # key=0，value=[0]代表 这个词为[0:0]即【去】
1: [1,2,4] # key=1,value=[1,2,4]代表有三个词，分别为[1:1],[1:2],[1:4],即北、北京、北京大学
2: [2]
3: [3,4]
4: [4]
5: [5]
}

实现方式如下（采用伪代码的形式讲述，有兴趣的朋友可以去GitHub看他的源码）：

def get_DAG(self, sentence):
	dag = {} # 最终生成的dag
	for k in range(len(sentense)):
		end_lst = [] # 结尾的position list
	    # 对每个position构造以该position开头的子串
		for j in range(k+1,len(sentence)):
			term = sentence[k:j]
			if term 在前缀词典，且词频>0:
				end_lst.append(j-1)
			elif term 在前缀词典，且词频=0:
				continue
			elif term 不在前缀词典中:
				# 说明有未登录词
				break
		dag[k] = end_lst
	return dag

动态规划查找最大概率路径, 找出基于词频的最大切分组合

在得到所有可能的切分方式构成的有向无环图后，我们发现从起点到终点存在多条路径，多条路径也就意味着存在多种分词结果，比如：

# 路径1
0 -> 1 -> 2 -> 3 -> 4 -> 5
# 分词结果1
去 / 北 / 京 / 大 / 学 / 玩
# 路径2
0 -> 1 , 2 -> 3 -> 4 -> 5
# 分词结果2
去 / 北京  /  大 / 学 / 玩
# 路径3
0 -> 1 , 2 -> 3 , 4 -> 5
# 分词结果3
去 / 北京  /  大学  /  玩
# 路径4
0 -> 1 , 2 , 3 , 4 -> 5
# 分词结果4
去 / 北京大学    /     玩
...

上一节构造的DAG是带权的，其权重为该词在前缀词典中的词频。我们的目标是，求得一个路径，使得其权重最大。

从源码可以看出，采用动态规划的方式对其进行求解（源码位置）：

其中，logtotal为构建前缀词频时所有的词频之和的对数值，目的是为了防止下溢问题。route含义为：（最大概率对数，最大概率对数对应的词语的最后一个位置）。
其状态转移方程为：
$$r_i=max(log\frac{w_{i\to j}}{Z}+r_j)，i\to j\in DAG$$
其中,$Z$是归一化函数，$i\to j$表示位置i到位置j的词，$w$表示该词的词频。

HMM识别未登陆词

关于HMM的原理，详见我的博客：概率图模型。

假设“去北京大学玩”中包含未登陆词，那么我们其实是试图构造如下的序列标注：

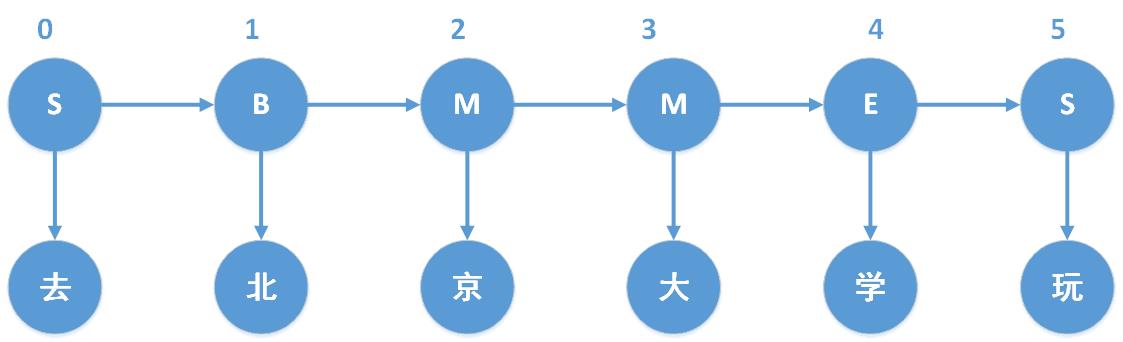
其中，B、M、E、S，分别表示Begin（这个字处于词的开始位置）、Middle（这个字处于词的中间位置）、End（这个字处于词的结束位置）、Single（这个字是单字成词）。

既然我们的目标是获取序列标注，那么自然是采用维特比算法求解。

已知观测序列$O$和$\lambda =(\pi ,A,B)$，求得最有可能出现的状态序列。

• 这里的观测序列自然是"去北京大学玩"
• 模型参数早已通过语料训练完成，存储于jieba/finalseg/下。
  prob_start.py 存储了已经训练好的HMM模型的状态初始概率表；
  prob_trans.py 存储了已经训练好的HMM模型的状态转移概率表；
  prob_emit.py 存储了已经训练好的HMM模型的状态发射概率表；

在概率图模型中已经列出维特比算法的原理：

其源码如下：

def viterbi(obs, states, start_p, trans_p, emit_p):
    V = [{}]  # tabular
    path = {}
    # 时刻t = 0，初始状态
    for y in states:  # init
        V[0][y] = start_p[y] + emit_p[y].get(obs[0], MIN_FLOAT)
        path[y] = [y]
    # 时刻t = 1,...,len(obs) - 1
    for t in xrange(1, len(obs)):
        V.append({})
        newpath = {}
        # 当前时刻所处的各种可能的状态
        for y in states:
            # 获取发射概率
            em_p = emit_p[y].get(obs[t], MIN_FLOAT)
            # 分别获取上一时刻的状态的概率，该状态到本时刻的状态的转移概率，本时刻的状态的发射概率
            # 其中，PrevStatus[y]是当前时刻的状态所对应上一时刻可能的状态
            (prob, state) = max(
                [(V[t - 1][y0] + trans_p[y0].get(y, MIN_FLOAT) + em_p, y0) for y0 in PrevStatus[y]])
            V[t][y] = prob
            # 将上一时刻最优的状态 + 这一时刻的状态
            newpath[y] = path[state] + [y]
        path = newpath

    # 最后一个时刻
    (prob, state) = max((V[len(obs) - 1][y], y) for y in 'ES')

    # 返回最大概率对数和最优路径
    return (prob, path[state])

关键词提取

采用tfidf和textrank进行关键词提取。

TF-IDF

TF-IDF（term frequency–inverse document frequency，词频-逆向文件频率）是一种用于信息检索（information retrieval）与文本挖掘（text mining）的常用加权技术。其字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。

它的主要思想是： 如果一个词在某篇文章中出现的词频很高，但是在其他文章中很少出现，则可以认为该词具有很好的区分能力，可以用作关键词。

tf(term frequency, 词频)：
$$t{f}_{i,j}=\frac{n_{i,j}}{{\sum }_k{n}_{k,j}}$$
其中，$n_{i,j}$表示在$d_j$文档中，词$i$出现的次数，${\sum }_k{n}_{k,j}$表示文档$d_j$中词的总数。

idf(inverse document frequency,逆文档频率)：
i d f i = l o g ∣ D ∣ ∣ { j : n i ∈ d j } ∣ + 1 idf_i = log \\frac{|D|}{|\\{j:n_i\\in d_j\\}|+1} idfi​=log∣{j:ni​∈dj​}∣+1∣D∣​
其中，分子表示文档的总数（有多少篇文档），分母表示包含词$n_i$的文档的数目。分母加1主要为了防止分母为0的情况。

tf-idf:
$$tfidf=tf\ast idf$$

TextRank

TextRank算法是一种基于图的用于关键词抽取和文档摘要的排序算法，由谷歌的网页重要性排序算法PageRank算法改进而来，它利用一篇文档内部的词语间的共现信息(语义)便可以抽取关键词，它能够从一个给定的文本中抽取出该文本的关键词、关键词组，并使用抽取式的自动文摘方法抽取出该文本的关键句。

pagerank:
（1）链接数量：如果一个网页被越多的其他网页链接，说明这个网页越重要，即该网页的PR值（PageRank值）会相对较高；

（2）链接质量：如果一个网页被一个越高权值的网页链接，也能表明这个网页越重要，即一个PR值很高的网页链接到一个其他网页，那么被链接到的网页的PR值会相应地因此而提高。
其计算公式如下：
$$s(v_i)=(1-d)+d\times \sum _{j\in in(v_i)}\frac{1}{|out(v_j)|}s(v_j)$$
$s(v)$表示网页的重要性，即pr值，d是阻尼系数，一般是0.85，$in(v)$是网页的入度，表示对所有指向该网页的网页；$out(v)$表示网页的出度， 1 ∣ o u t ( v j ) ∣ s ( v j ) \\frac{1}{|out(v_j)|} s(v_j) ∣out(vj​)∣1以上是关于结巴分词原理的主要内容，如果未能解决你的问题，请参考以下文章

结巴分词原理

结巴中文分词原理分析2

结巴分词获取关键词时怎么过滤掉一些停用词

结巴分词

python中文分词，使用结巴分词对python进行分词

python结巴(jieba)分词