重要力扣每日一题.NO141.环形链表

Posted 2021-11-23 东条希尔薇

画图讲解和源代码已上传至我的码云

原题地址

目录

• 投票直通车

题目描述

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

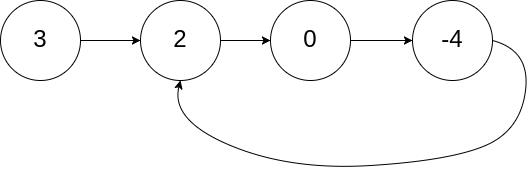
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

思路求解

笔者先说一句：向想出这个算法的大佬致敬！能想出这个办法，真的是太聪明了！

这个算法非常想我们高中物理必修1学过的追及相遇问题

具体思路如下：

我们定义一对快慢指针

快的每次走两步，慢的每次走一步

这样，它们两个如果入了环，快的一定是会追上慢的

如果快的和慢的相遇了，则链表就有环，

如果没有相遇，而是fast走向NULL了，链表就没有环

什么？你问我为什么快的一定会追上慢的？这要问你高中物理老师了，这个我帮不了你(doge)

画图求解

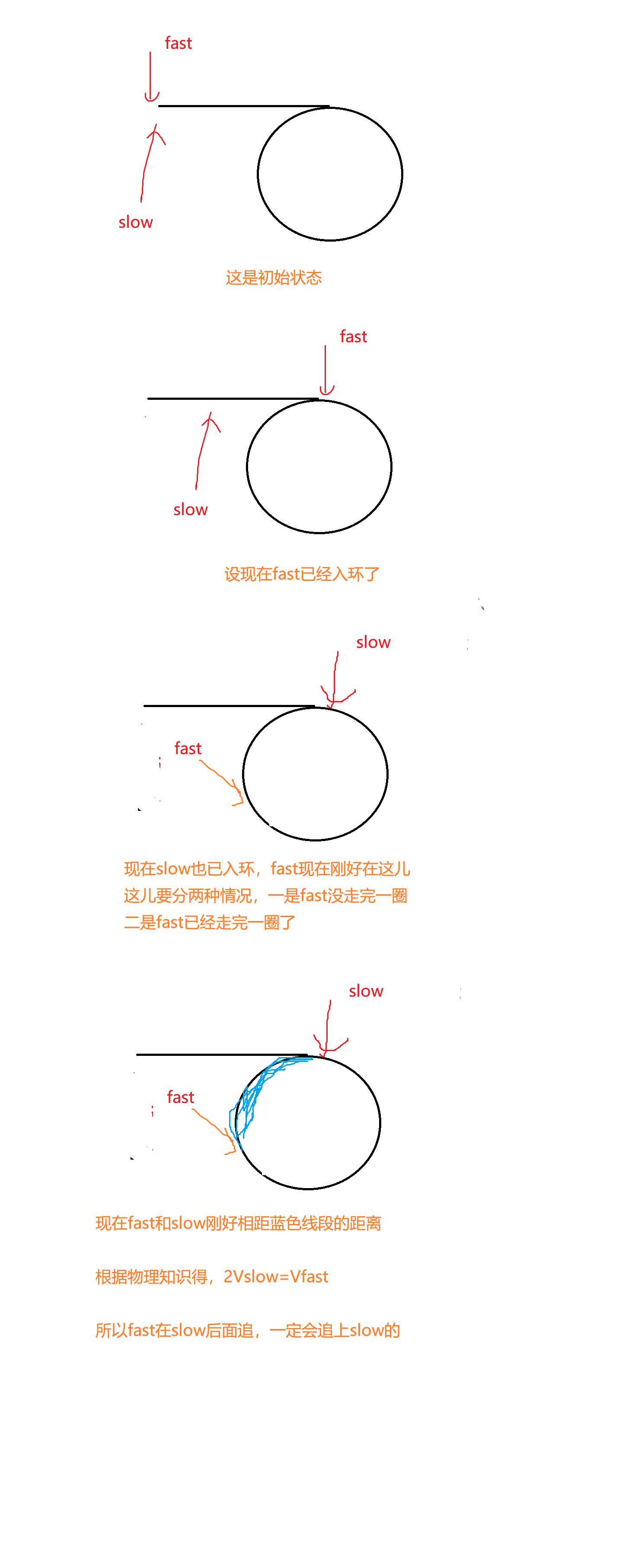
代码实现（c语言）

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow=head,*fast=head;
    while(fast&&fast->next)//判断有没有环的条件
    {
        
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)//相等，证明有环了
            return true;
        
    }
    
    return false;
}

但其实这个追及问题跟物理上的还不太一样，链表这里的运动轨迹是离散的点，而物理中的追及，它们的运动轨迹是连续的

所以有了以下的问题
思考问题（重要）

1. 为什么这个算法成立？给出数学证明
2. 为什么一定要2Vslow=fast?能不能推广到nVslow=fast?(即fast的速度是slow的任意倍)

---

第一个问题的证明：

• fast一定先进环，slow此时走了圈外的1/2（这条为公理，不证明）
• slow进环后，fast已经走了一段，与slow相距多少和圈的大小有关，我们可以先设为x

那么，它们之间的距离会存在以下关系

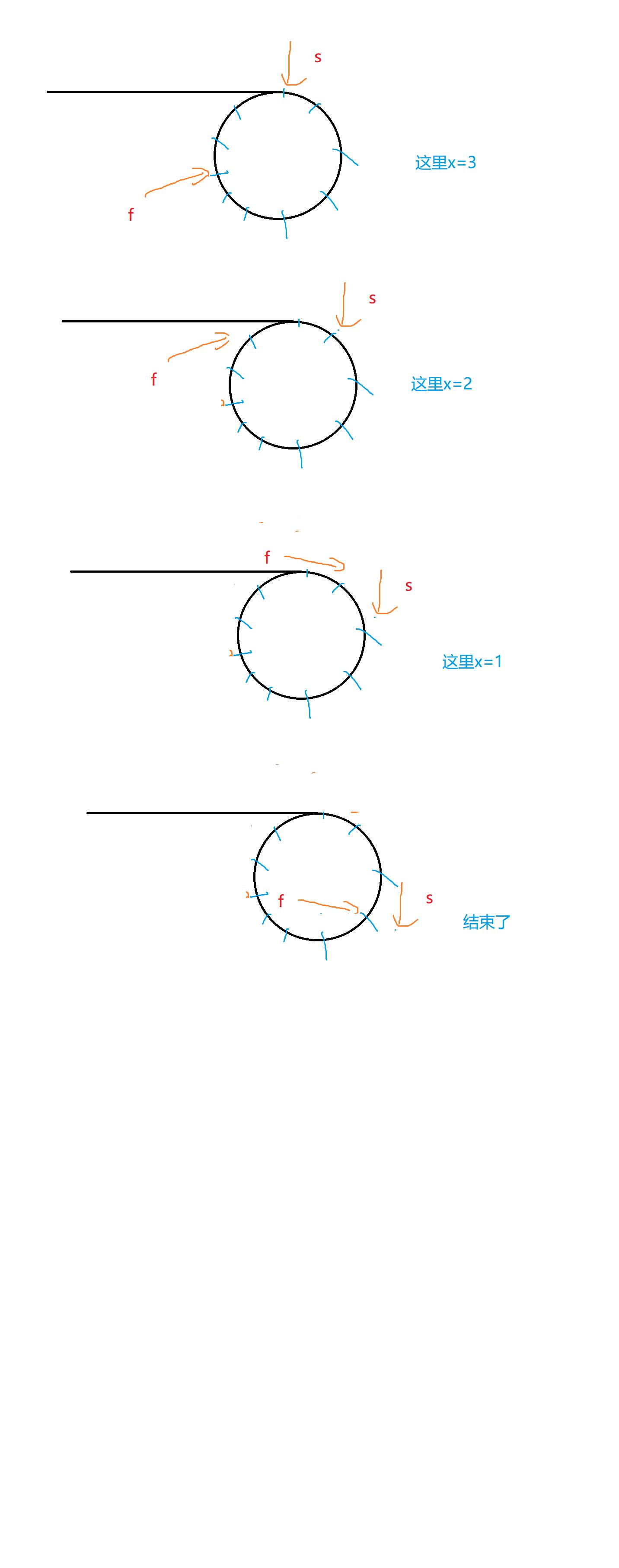
初始：x
遍历一次：x-1
遍历两次：x-2

最后一次：1，
结束：0
。。。

我们可以发现，它们之间的距离每次都是-1，所以能够保证它们的距离一定能减到0

第二个问题的证明

结论：不一定

我们在这里设它们之间的速度为3倍关系

这样，可以得到它们的速度差为2，即它们之间的距离每次都减2

它们的距离会有以下关系

x
x-2
x-4
.
.
.
2?
1?

最后两项值得考究

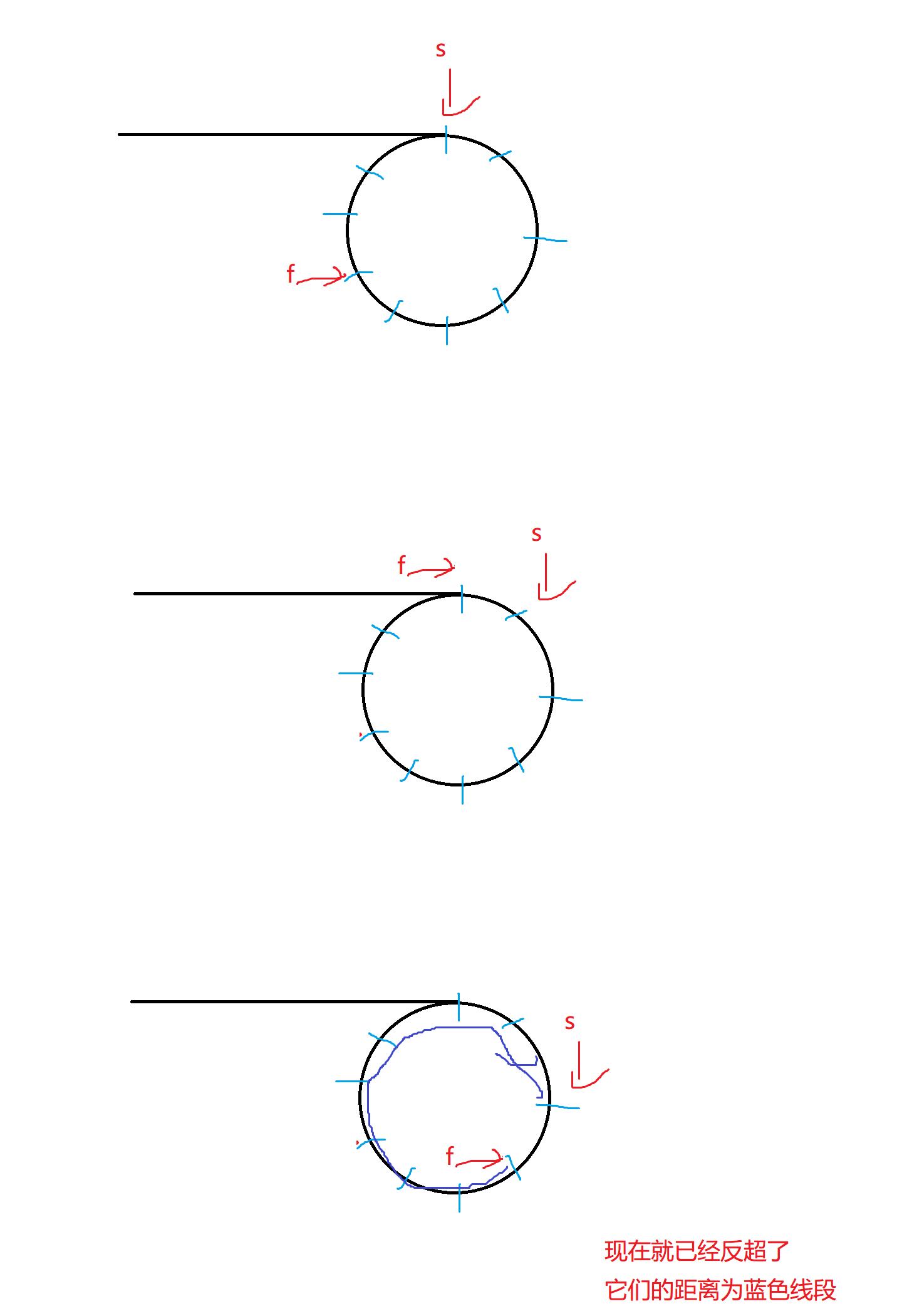
因为我们可以发现，当它们之间的距离为x-2时，这时候再减二，就刚好相遇了

但是当距离为x-1时，这时再减二，它们之间的距离就是-1，这说明slow已经反超了fast!

再经过简单的数学推理，可以得出结论

当距离是-1后，它们之间的距离(大圈举例如果还是奇数，将永远追不上了)

画图求解：

投票直通车