matlab电动汽车路径优化——考虑充电

Posted 2021-11-23 张叔zhangshu

概述

基于电动汽车电量消耗特性，考虑电动车里程、载重、顾客服务时间窗等约束，建立以配送总成本最小为目标的电动车调度优化问题模型；利用自然数编码的遗传算法，求解出电动车的配送路线以及车辆的充电计划。
由于电动汽车是靠电能驱动，故充电是电动汽车在行驶过程中必须面对的问题之一。当电池电量不足以完成剩余的配送任务时，电动车需要进入到邻近的充电站进行充电，以供其完成剩余的配送任务。在本文中，充电站采用的是快速充电方式，使电动车在30 min左右就可以完成充电。但是由于充电站可能不位于车辆既定的行驶线路上，车辆会发生行驶偏移，因而带来配送中心总成本的增加。由于电动车配送过程需要考虑电动车的续驶里程、电池电量、充电站位置、客户服务的时间窗和车辆额定载重等诸多因素，为使问题更加简洁明了，预先进行以下假设

1. 只有一个配送中心，所有车辆从配送中心出发最后返回原配送中心；
2. 客户的数量、客户的位置、客户服务的时间窗及每个客户的需求量均已知，且车辆的总载重不得超过车辆的额定载重；
3. 配送车辆从配送中心出发，电池为满电状态，且在货物装卸过程中不存在电量的消耗；
4. 货物流向为单向，只进行配送货物不进行收集货物；
5. 电动车的额定续驶里程和充电时间均已知。

符号及变量定义

C0为总费用；
Cfk为车辆k的固定费用；
Ctk为车辆k的行驶费用；
Cmk为车辆k的充电费用；
Cpk为车辆k的早到或晚到产生的惩罚费用；
O为配送中心；
K为车辆集合；
M为充电站集合；
N 为客户点集合；
L L =O ∪ M ∪ N为配送中心、充电站、客户点的集合，；
speed为车辆额定行驶速度；
P为电动车额定电量；
P′ik为车辆k到达集合点i时电量，i ∈ L；
P′′ik为车辆k离开集合点i时电量，i ∈ L；
ei为客户点i的最早服务时间；
li为客户点i的最晚服务时间；
epu为表示车辆早于时间窗到达造成的等待惩罚成本；
lpu为表示车辆晚于时间窗到达的惩罚成本；
t′i为车辆到达集合点i的时刻，i ∈ L；
t′′i为车辆离开集合点i的时刻，i ∈ L；
tfi为车辆在集合点i卸货、充电时间，i ∈ L；
twi为车辆在客户点处等待服务时间，i ∈ N；
Djk为车辆k到达点j时的剩余电量里程；
di j为客户点i和j之间的距离；
Wmax为车辆额定载重量；
Dmax为车辆最大行驶距离；
Ed为电动车电量单位里程消耗；
Wi为车辆载重量；
车辆路径问题属于NP-hard问题，该问题约束条件繁多，规模较大。遗传算法具有强大的搜索能力和自适应性，因此遗传算法对于求解较为复杂的大型网络车辆调度问题具有较好的效果。选用遗传算法求解电动汽车调度方案模型。

案例及结果分析

设某配送案例中，有1个配送中心，4个充电站，充电时间为0.3 h，5辆相同型号的配送车辆共服务50个客户。且配送中心、充电站、客户的坐标、客户点需求和服务时间窗均已知。车辆从配送中心出发，考虑到有充电需求，所以应合理安排路径，完成配送任务。



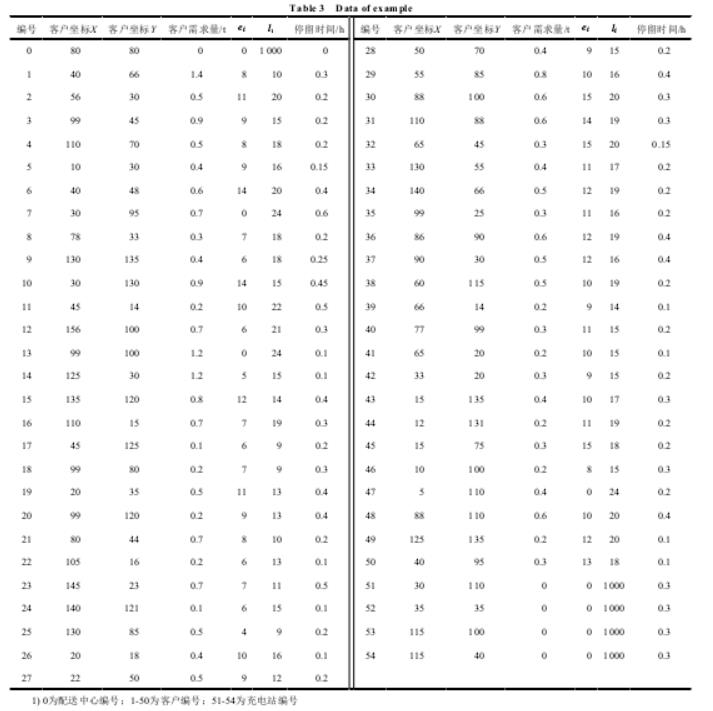
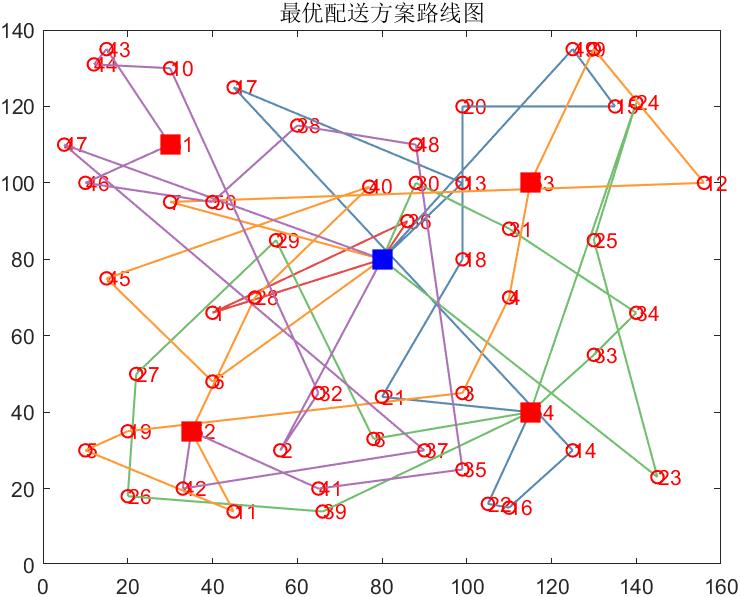
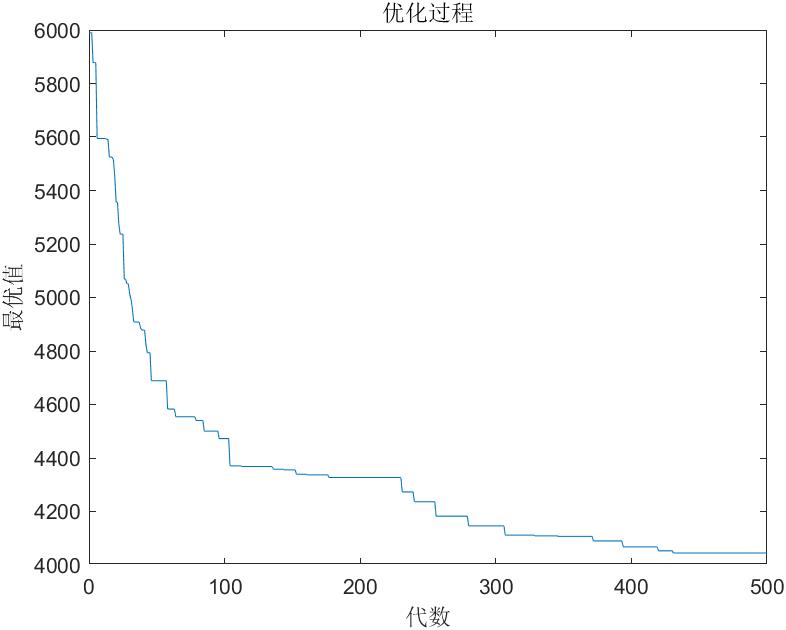
本文基于电动车电量特性，充分考虑电动车电量消耗、里程约束、载重约束、顾客服务约束等，建立以配送总成本最小为目标的基于电量消耗带时间窗的电动汽车路径规划问题模型，对模型中配送中心总成本、电动车电量的单位里程能耗、电动车停留时间、电动车行驶时间等进行分析；采用遗传算法首先求解出该模型中配送车辆的最佳配送方案，该配送方案包括车辆的行驶路线和行驶过程中的充电计划，优选出配送车辆惩罚成本最小时的最优发车时刻，从而得到车辆到达每一客户点及充电站的时刻。最后结合算例，计算出最佳配送路线、充电方案、最优发车时刻以及最小总配送成本，验证了该模型和算法的有效性和正确性。但本文只研究了基于时间窗的电动汽车调度问题，而现实生活中，道路实际情况，以及顾客的服务需求都是动态变化的。如何根据实际的动态要求，将是今后进一步研究的内容。

主程序

clear
clc
close all
tic
%% 用importdata这个函数来读取文件
load('c101');
shuju=c101;
bl=0;
cap=6;                                                        %车辆最大装载量
%% 提取数据信息
E=shuju(1,5);                                                    %配送中心时间窗开始时间
L=shuju(1,6);                                                    %配送中心时间窗结束时间
zuobiao=shuju(:,2:3);                                       %所有点的坐标x和y
customer=zuobiao(2:end-4,:);                                       %顾客坐标
cusnum=size(customer,1);                                         %顾客数
v_num=5;                                                        %车辆最多使用数目
demands=shuju(2:end,4);                                          %需求量
a=shuju(2:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=shuju(2:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
s=shuju(2:end,7);                                                %客户点的服务时间
h=pdist(zuobiao);
dist=squareform(h);    
dist=dist;%距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
alpha=100000;                                                       %违反的容量约束的惩罚函数系数
belta=15;%违反时间窗约束的惩罚函数系数
belta2=10;%违反系数
chesu=50;
NIND=300;                                                       %种群大小
MAXGEN=500;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum+v_num-1;                                %染色体长度=顾客数目+车辆最多使用数目-1
%% 初始化种群
Chrom=InitPopCW(NIND,N,cusnum,a,demands,cap);     %构造初始解
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
[VC,NV,TD,VCC,GS]=decode(Chrom(1,:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
disp(['车辆使用数目：',num2str(NV),'，车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
preObjV=min(ObjV);
while gen<=MAXGEN
    %% 计算适应度
    ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
    line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)%画图 最优函数
    preObjV=min(ObjV);
    FitnV=Fitness(ObjV);
    %% 选择
    SelCh=Select(Chrom,FitnV,GGAP);
    %% OX交叉操作
    SelCh=Recombin(SelCh,Pc,v_num);
    %% 变异
    SelCh=Mutate(SelCh,Pm);
    %% 重插入子代的新种群
    Chrom=Reins(Chrom,SelCh,ObjV);
    %% 打印当前最优解
    ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD,bestVCC,bestGS]=decode(Chrom(minInd(1),:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\\n')
    %% 更新迭代次数
    gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp('最优解:')
bestChrom=Chrom(minInd(1),:);
[bestVC,bestNV,bestTD,bestVCC,bestGS]=decode(bestChrom,cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
[sumTD,everyTD,n]=travel_distance(bestVCC,dist);
disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
disp('-------------------------------------------------------------')
[cost]=costFuction(bestVC,a,b,s,L,dist,demands,cap,alpha,belta,belta2,chesu,bl,bestGS);
%% 画出最终路线图
draw_Best(bestVCC,zuobiao);

数据c101

0	80	80	0	0	1000	0
1	40	66	1.40000000000000	8	10	0.300000000000000
2	56	30	0.500000000000000	11	20	0.200000000000000
3	99	45	0.900000000000000	9	15	0.200000000000000
4	110	70	0.500000000000000	8	18	0.200000000000000
5	10	30	0.400000000000000	9	16	0.150000000000000
6	40	48	0.600000000000000	14	20	0.400000000000000
7	30	95	0.700000000000000	0	24	0.600000000000000
8	78	33	0.300000000000000	7	18	0.200000000000000
9	130	135	0.400000000000000	6	18	0.250000000000000
10	30	130	0.900000000000000	14	15	0.450000000000000
11	45	14	0.200000000000000	10	22	0.500000000000000
12	156	100	0.700000000000000	6	21	0.300000000000000
13	99	100	1.20000000000000	0	24	0.100000000000000
14	125	30	1.20000000000000	5	15	0.100000000000000
15	135	120	0.800000000000000	12	14	0.400000000000000
16	110	15	0.700000000000000	7	19	0.300000000000000
17	45	125	0.100000000000000	6	9	0.200000000000000
18	99	80	0.200000000000000	7	9	0.300000000000000
19	20	35	0.500000000000000	11	13	0.400000000000000
20	99	120	0.200000000000000	9	13	0.400000000000000
21	80	44	0.700000000000000	8	10	0.200000000000000
22	105	16	0.200000000000000	6	13	0.100000000000000
23	145	23	0.700000000000000	7	11	0.500000000000000
24	140	121	0.100000000000000	6	15	0.100000000000000
25	130	85	0.500000000000000	4	9	0.200000000000000
26	20	18	0.400000000000000	10	16	0.100000000000000
27	22	50	0.500000000000000	9	12	0.200000000000000
28	50	70	0.400000000000000	9	15	0.200000000000000
29	55	85	0.800000000000000	10	16	0.400000000000000
30	88	100	0.600000000000000	15	20	0.300000000000000
31	110	88	0.600000000000000	14	19	0.300000000000000
32	65	45	0.300000000000000	15	20	0.150000000000000
33	130	55	0.400000000000000	11	17	0.200000000000000
34	140	66	0.500000000000000	12	19	0.200000000000000
35	99	25	0.300000000000000	11	16	0.200000000000000
36	86	90	0.600000000000000	12	19	0.400000000000000
37	90	30	0.500000000000000	12	16	0.400000000000000
38	60	115	0.500000000000000	10	19	0.200000000000000
39	66	14	0.200000000000000	9	14	0.100000000000000
40	77	99	0.300000000000000	11	15	0.200000000000000
41	65	20	0.200000000000000	10	15	0.100000000000000
42	33	20	0.300000000000000	9	15	0.200000000000000
43	15	135	0.400000000000000	10	17	0.300000000000000
44	12	131	0.200000000000000	11	19	0.200000000000000
45	15	75	0.300000000000000	15	18	0.200000000000000
46	10	100	0.200000000000000	8	15	0.300000000000000
47	5	110	0.400000000000000	0	24	0.200000000000000
48	88	110	0.600000000000000	10	20	0.400000000000000
49	125	135	0.200000000000000	12	20	0.100000000000000
50	40	95	0.300000000000000	13	18	0.100000000000000
51	30	110	0	0	1000	0.300000000000000
52	35	35	0	0	1000	0.300000000000000
53	115	100	0	0	1000	0.300000000000000
54	115	40	0	0	1000	0.300000000000000
如需帮助zhangshu2274