kmp算法

Posted 2021-11-23 正义的伙伴啊

KMP算法

写OJ时做到字符串匹配问题，用暴力算法结果超出时间限制了，其实早就知道这种问题可以用kmp算法解决，但是我一直懒得学，于是借助这个OJ来记录一下学习kmp算法 的一些个人理解

文章目录

• KMP算法
• • 字符串匹配问题
  • 先从暴力匹配算法说起
  • kmp数组的整体思路
  • next数组的实现
  • 实现kmp算法

字符串匹配问题

实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

说明：

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。

oj链接

几个名词：

• 主串：带匹配的字符串，这里设为char *s
• 模式串：要与主串进行匹配的字符串，这里设为char *p

先从暴力匹配算法说起

这个算法思路很简单：

1. 首先将主串的每个字符与模式串的第一个字符进行比较，如果不匹配就继续遍历主串，匹配的话就主串和模式串一起遍历（但是要记住主串进入遍历的位置）。直到遇到不同的字符，或者是模式串结束。
2. 判断每次同时遍历模式串结束的位置，如果模式串走到结尾则说明主串与模式串匹配成功，反之就要回溯模式串，继续拿模式串首字符与主串进行比较。
   
   
   
   

这就是暴力匹配的基本思路，首先要明确几点：

1. 首先是回溯的是模式串！模式串在程序没有结束的情况下每次都回溯到首字符的位置。
   4.最后检查是否匹配成功的重要依据是模式串是否走到结尾，因为两个串同时遍历，遇到不相等的或走到结尾 就会停止同时遍历！

代码：

int strStr(char * haystack, char * needle){
    if(*needle =='\\0')
    return 0;
    if(*haystack =='\\0')
    return -1;
    
    int size1=strlen(haystack);
    int size2=strlen(needle);
    
    for(int i=0;i<=size1-size2;i++) //这里的循环只用进行size1-size2+1次，因为当i>size1-size2时，两个串同时遍历，主串会比模式串先到达末尾
    {
        if(haystack[i]==needle[0])
        {
            int x=i,y=0;
            for( y=0;y<size2;x++,y++)
            {
                if(haystack[x]!=needle[y])
                break;
            }
            if(y==size2)  //判断模式串结束的位置
            return i;
        }
    }
    return -1;
}

kmp数组的整体思路

KMP算法 是建立在暴力匹配的思路之上的，那区别又在什么地方呢？
主要是在回溯的这一个过程上，暴力匹配算法 每次模式串回溯都是回退到首字符的位置，而kmp算法则会根据模式串的性质和每次遍历结束的位置来确定每次回溯的位置
聚个简单的例子：

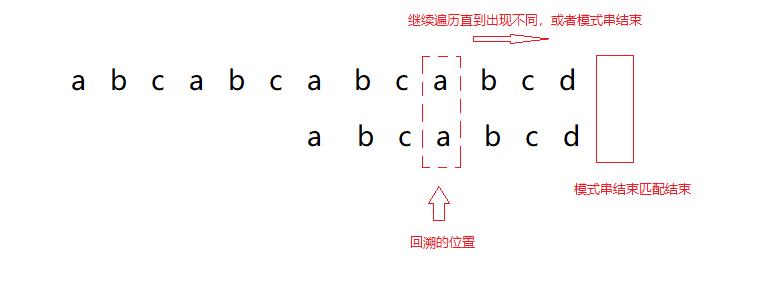
• 第一次遍历在结尾出现匹配失败，按照kmp算法应该如何回溯呢？那就要对出现不匹配字符前面的字符串进行分析！
  
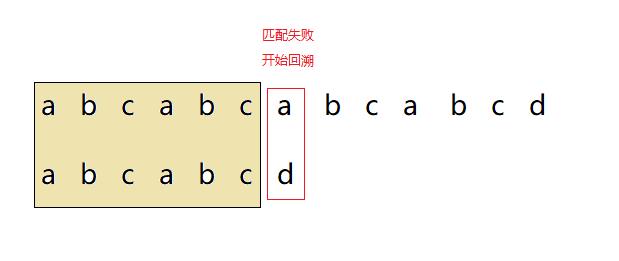
• 我们发现字符串abcabc（遍历不匹配的位置前面的字符串）这个字符串里面有相同的字符段，这些字符段是字符串内部重复，我们把前面的abc叫做前缀，后面的abc叫做后缀，而我们要找的就是前缀与后缀相等的最大字符段！
  
• 下面就体现了这些字符段的作用了。找到最大相等前后缀后，我们就找到了回溯的位置：也就是前缀的下了一个字符

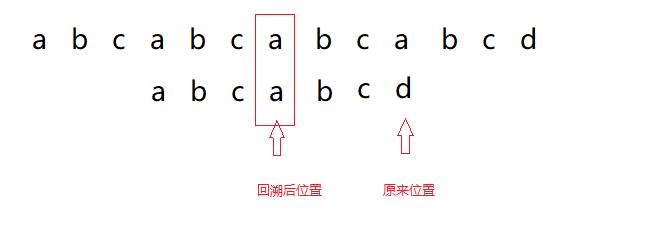
• 找到回溯的位置后我们就从回溯的位置主串与模式串继续向后遍历，直到遇到不相等的，或者模式串结束

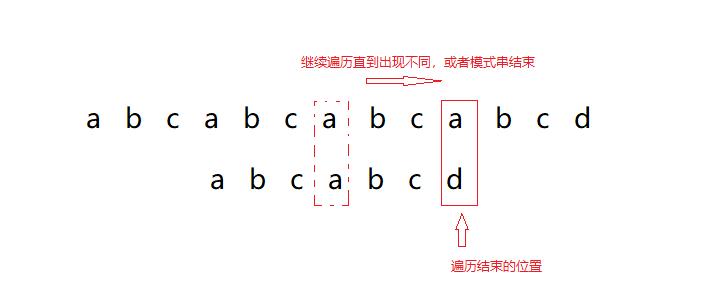
• 重复上述的步骤
  
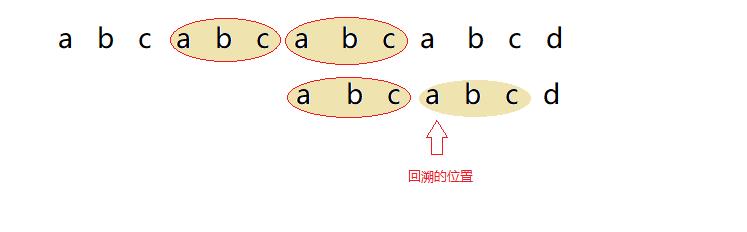
• 最终得到答案

那么每次回溯的位置应该如何确定？
这是kmp算法的一个核心问题，首先我们要清楚回溯的位置与 每次遍历不匹配的位置 和 每次遍历不匹配的位置前面的字符串有关。也就是说随着不匹配位置的不同每次回溯的位置也不同。这里我们可以用一个数组来储存回溯的位置，而数组的下标是 每次遍历不匹配的位置，我们把这个数组叫做next数组，这里我们先不管next数组如何求，这里我们只需要知道输入 不匹配的位置就可以从next数组中找到回溯的位置就行了！

这就是对kmp算法的一个总览，大体思路是：

• 主串与模式串同时向后遍历，直到遇到不同的字符或模式串结束。
• 假设不匹配字符的下表是j，则回溯位置为k=next[j]。然后从回溯位置继续两个串进行遍历匹配，重复步骤1,2（但是这里还有一个特殊情况就是主串与模式串第一个字符就不匹配的情况，这种情况要单独处理，等到next数组讲完再处理）
• 模式串如果被遍历结束这说明找到了主串中与模式串匹配的字符段
  如果在主串遍历完模式串还没出现过遍历到末尾，则主串中不存在模式串

next数组的实现

上面已经提到了next数组的下标的含义和对应的下标所储存的值得含义，接下来就要说明如何求解next数组。

• 首先要了解一下前后缀
  
  注意一下前后缀是不包括字符串本身的，如果字符串为n个，最大前缀或最大后缀为n-1

最大相等前后缀： 也就是存在一个前缀和一个后缀相等，且找不出比这个前后缀更长的且相等的前后缀（这个也就是回溯时的最大位移）

• 然后我们再明确一下next数组的含义：
  下标：每次遍历不匹配的位置
  下标所对应的next数组的值：储存的回溯的位置
  回溯的位置：也就是每次遍历不匹配的位置前面的字符串 的最大相等前后缀 的下一个字符的下标

• 如何求解next数组

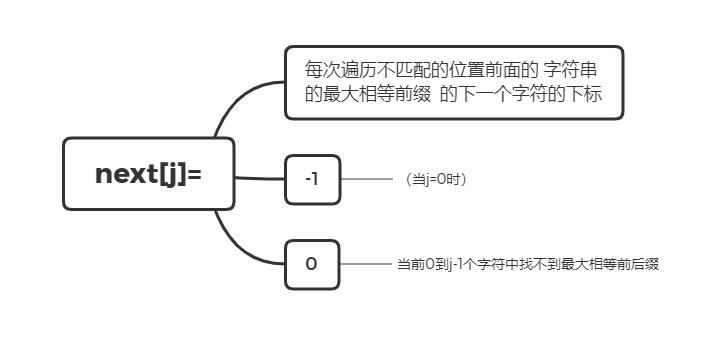
这里把j===0时设置为一个特殊值-1，这是为了区分next[j]==0（也就是前后缀相等不存在）的情况。
第一种情况：是首字符就与主串不匹配，无需在进入后面的遍历，只需要拿首字符与主串的下一个字符进行比较，直到遇到相等的为止

第二种情况：是回溯的位置是模式串的首字符位置，但是模式串回溯到首字符位置之后还要和主串所指向的字符进行比较（注意第一种情况是和主串指向字符的下一个字符进行比较），如果不相等下一次回溯的位置k=next[0]=-1也就是第一种情况。
所以这里j==0这种情况要单独处理

next数组的性质：（以模式串char *p=ababcaabc为例）

首先有前面的性质可以知道next[0]=-1;

然后我们可以推出next[1]=0;这两个数值是定值（如果存在的话），因为前缀和后缀是不包括字符串本身，而下标为1时前面的字符串长度为1，是不存在前后缀的。

1. 假设我们要求下表为j处的next的值，首先要知道j-1处的next值，因为求下标为j处的next值也就是求0到j-1字符串的最大相等前后缀，0到j-1字符串可以拆成0到j-2加上j-1处的字符
   

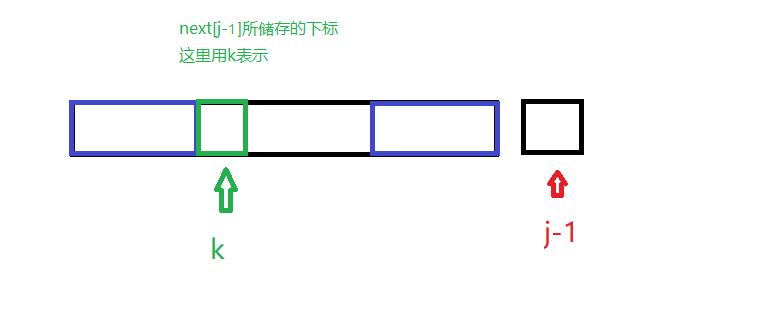
• 如果p[j-1]==p[next[p-1]]或者是p[j-1]==p[next[p-1]]

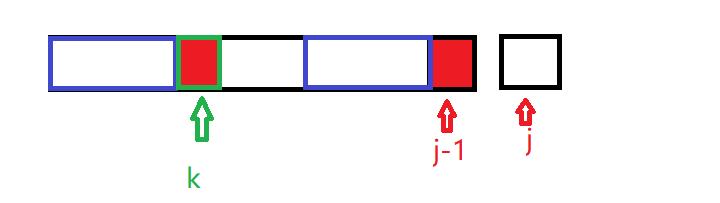
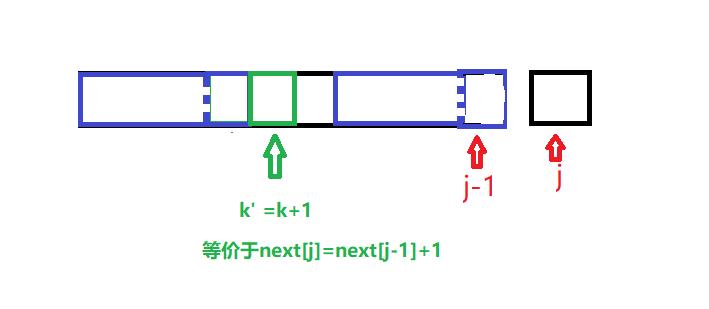
由此推出关系：next[j]=next[j-1]+1

• 如果如果p[j-1]！=p[next[p-1]]或者是p[j-1]！=p[next[p-1]]

这时候因为next数组的值是最大相等前后缀的前缀的下一个字符，由于上面的失败告诉我们最大相等前后缀的前缀是不行的，所以我们应该把注意力放到k之前的字符串里面去寻找，按照上面的思路得到褐色框部分为两个相等的字符段

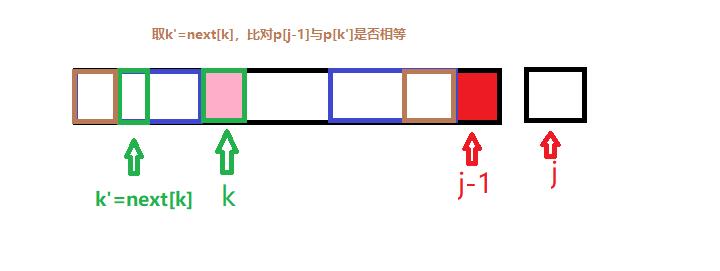
如果p[j-1]==p[k'] 则next[j]=k'+1
如果不相等，就继续重复上面步骤：取k''=next[k'] 并比较p[j-1]==p[k'']

• 上述循环结束的标志是当某一次：kn'=next[k(n-1)']==-1也就是当p[j-1]!=p[0]时，这时就不存在最大相等前后缀，所以next[j]==0

next数组实现代码：

void buildNext(char* s, int* next)  // 在函数外事先开好next数组的空间
{
	int size = strlen(s);
	next[0] = -1;
	for (int i = 1; i < size; i++)
	{
		if (i==1 || s[next[i - 1]] == s[i - 1])  //i=1是next[i]必然等于0，但是由于next[0]==-1所以需要特殊处理
		{
			next[i] = next[i - 1] + 1; //进入循环也就是一开始就相等的情况，直接套用关系next[j]=next[j-1]+1
			continue;
		}
		else
		{    //此处就是不相等的情况，要不断的迭代kn'=next[k(n-1)']
			int k = next[i - 1];      
			while (k >= 0)   
			{
				if (s[k] == s[i - 1])
				{
					next[i] = k + 1;
					break;
				}
				k = next[k];
			}
            if (k < 0)  //走到这步只有两种情况：1.是一件next[i]已经赋值完成，此时k必然大于0
			{                             // 2.是k==-1时还没有完成赋值，这时就说明不存在最大相等前后缀
				next[i] = 0;
			}
		}
	}
}

实现kmp算法

next数组求解出来之后，kmp算法也就差不多完成了：
这时我们再看一遍kmp算法的思路：

• 主串与模式串同时向后遍历，直到遇到不同的字符或模式串结束。

• 假设不匹配字符的下表是j，则回溯位置为k=next[j]。然后从回溯位置继续两个串进行遍历匹配，重复步骤1,2（如果k==next[0]==-1则是首字符就与主串不匹配，无需在进入后面的主串与模式串同时遍历，只需要拿首字符与主串的下一个字符进行比较，直到遇到相等的为止）

• 模式串如果被遍历结束这说明找到了主串中与模式串匹配的字符段

如果在主串遍历完模式串还没出现过遍历到末尾，则主串中不存在模式串

整个kmp算法的核心依据是： 观察模式串是否在程序的运行过程中走到字符串结尾

直接放上代码：

void buildNext(char* s, int* next)
{
	int size = strlen(s);
	next[0] = -1;
	for (int i = 1; i < size; i++)
	{
		if (i==1 || s[next[i - 1]] == s[i - 1])
		{
			next[i] = next[i - 1] + 1;
			continue;
		}
		else
		{
			int k = next[i - 1];
			while (k >= 0)
			{
				if (s[k] == s[i - 1])
				{
					next[i] = k + 1;
					break;
				}
				k = next[k];
			}
            if (k < 0)
			{
				next[i] = 0;
			}
		}
	}
}


int kmp(char* s,char* p)
{

	int size = strlen(p);
	int* next = (int*)malloc(size * sizeof(int));
	buildNext(p, next);


	int i = 0, j = 0;
	while (s[i] != '\\0' && p[j] != '\\0')
	{
		if (s[i] == p[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];

			if (j == -1)
			{
				i++;
				j = 0;
			}
		}
	}
	free(next);
	if (p[j])   //观察模式串是否在程序的运行过程中走到字符串结尾
		return -1;  //未走到结尾上面的while循环因为主串走到结尾而提前结束，所以不存在匹配的模式串
	else
		return i - strlen(p);//模式串在程序的运行过程中走到字符串结尾,返回匹配的位置
}

总结：
kmp实际上是一个以空间换效率的做法，避免了回溯过程中所浪费的时间复杂度。