机器学习带你搞懂什么是特征工程？(特征抽取&特征预处理&特征选择&数据降维)

Posted ZSYL

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习带你搞懂什么是特征工程？(特征抽取&特征预处理&特征选择&数据降维)相关的知识，希望对你有一定的参考价值。

带你搞懂什么是特征工程？

特征工程

什么是特征工程：

特征工程是将原始数据转换为更好地代表预测模型的潜在问题的特征的过程，从而提高了对未知数据的模型准确性。

比如原始数据可能非常庞大，但是对我们有用的数据可能就是其中的几项，而其他项留着可能会影响我们的结果，因此可以进行特征选择。或者比如我们想要在把数据放到算法中进行计算的时候，一些文本数据先要转换成数字类型的数据，这时候就需要进行one-hot编码，等等。所有这些在把数据输入算法之前做的事情，都可以统称为特征工程。

特征工程的意义：

  1. 更好的特征会有更强的鲁棒性（稳定性）。
  2. 更好的特征只需用简单模型。
  3. 更好的特征会有更准确的结果。

特征抽取

在数据进入算法之前，先需要对数据进行一些特征抽取。以下是特征处理中常用到的方法：

字典特征抽取：

字典特征抽取，就是针对一系列字典中的数据进行抽取。示例代码如下：

from sklearn.feature_extraction import DictVectorizer
fruits = [{"fruit":"苹果","price":5},{"fruit":"橘子","price":5.9},{"fruit":"菠萝","price":9.9}]
vect = DictVectorizer()
result = vect.fit_transform(fruits)
print(result)
print(result.toarray())
print(vect.get_feature_names())
print(type(result))

其中result返回的是一个sparse矩阵，是scipy库中的数据类型。sparse的特点是可以节省内存，因为他只会记录result.toarray()这个列表中哪些位置出现了非0的值，以及具体的值。

常用方法：

  • fit_transform(X)：应用并转化列表X。
  • inverse_transform：将numpy数组或者sparse矩阵转换成列表。
  • get_feature_names()：获取fit_transform后的数组中，每个位置代表的意义。
  • toarray()：将sparse矩阵转换成多维数组。

One-hot编码：

机器学习的算法是没法针对字符串进行运算的。所以需要将字符串转换成数据类型。比如fruits的数据，转换成One-hot编码就是：

苹果橘子菠萝price
1005
0105.9
0019.9

而toarray()返回回来的就是one-hot编码的数组。

文本特征抽取：

文本的特征提取应用于很多方面，比如说文档分类、垃圾邮件分类和新闻分类。那么文本分类是通过词是否存在、以及词的概率（重要性）来表示。

文档中词出现的个数：

文本特征抽取，使用的是sklearn.feature_extraction.text.CountVectorizer

示例代码如下：

vect = CountVectorizer()
result = vect.fit_transform(['life is short,i need python','life is long,i do not need python'])
print(result)
print(result.toarray())
print(vect.get_feature_names())

其中，单个字母比如i是不会被当作一个单词进行抽取的。并且他的抽取规则是按标点符合或者是空格进行划分。因此这种默认的分词方式是不符合中文需求的。

中文分词：

如果想要统计中文中某些词出现的次数，那么先要对中文进行分词，这时候就需要用到一个第三方的开源库jieba分词。通过pip/conda install jieba即可安装。用法跟之前是一样的：

def countvect():
  word1 = "周密说，受到影响的应该说是某些特定领域的产品，不是全部的产品。"
  word2 = "装假固然不好，处处坦白，也不成，这要看是什么时候。和朋友谈心，不必留心，但和敌人对面，却必须刻刻防备，我们和朋友在一起，可以脱掉衣服，但上阵要穿甲。"
  word3 = "伟大的成绩和辛勤的劳动成正比例，有一分劳动就有一分收获，日积月累，从少到多，奇迹就可以创造出来。"

  punct = set(u''':!),.:;?]}¢'"、。〉》」』】〕〗〞︰︱︳﹐､﹒
﹔﹕﹖﹗﹚﹜﹞！），．：；？｜｝︴︶︸︺︼︾﹀﹂﹄﹏､～￠
々‖•·ˇˉ―--′’”([{£¥'"‵〈《「『【〔〖（［｛￡￥〝︵︷︹︻
︽︿﹁﹃﹙﹛﹝（｛“‘-—_…''')
  filterpunt = lambda s: ''.join(filter(lambda x: x not in punct, s))

  con1 = " ".join(jieba.cut(filterpunt(word1)))
  con2 = " ".join(jieba.cut(filterpunt(word2)))
  con3 = " ".join(jieba.cut(filterpunt(word3)))

  vect = CountVectorizer()
  result = vect.fit_transform([con1,con2,con3])
  print(result)
  print(result.toarray())
  print(vect.get_feature_names())

tf-idf文本抽取：

tf-idf（英语：tf(term frequency) idf(inverse document frequency)）是一种用于信息检索与文本挖掘的常用加权技术。tf-idf是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。
假如现在总共有1000个文档，“共享”这个词在500个文档中出现了，并且A文档中总共有800个词，“共享”出现了12次，那么tf-idf的值为：(12/800)*lg(1000/500)。示例代码如下：

from sklearn.feature_extraction.text import TfidfVectorizer
def tfidf():
    word1 = "共享单车确实烧钱，但这在中国创业圈里很常见，从打车到外卖都干过，雷布斯也语重心长，“创业还是要有烧不完的钱”，只不过共享单车烧得既没品味，也没技术含量，最后还引火烧身，几十亿美元落得这个结局，谁都没想到。"
    word2 = "在人工智能已经深入生活的今天，社会上不乏“人工智能威胁论”，担忧机器人会“反噬”人类。在这篇文章里，李开复博士讨论了人工智能技术未来发展所带来的几个更真切和亟待解决的问题：全球性的失业问题及可能产生的全球性经济失衡和贫富差距。"
    word3 = "从2009年到现在，鲨鱼投资者虽还在股海遨游，但胆子越来越小。折腾了N年，发现股票超出了我的认知范围，了解一家公司，难！股票行情，波动太大，小心脏受不了"
    tf = TfidfVectorizer()
    con1 = " ".join(jieba.cut(filterpunt(word1)))
    con2 = " ".join(jieba.cut(filterpunt(word2)))
    con3 = " ".join(jieba.cut(filterpunt(word3)))
    result = tf.fit_transform([con1,con2,con3])
    print(result)
    print(tf.get_feature_names())

tfidf()

特征预处理：

特征预处理是采用特定的统计方法（数学方法）将数据转化成算法要求的数字。

  1. 数值型数据：
    • 归一化（将原始数据变换到[0,1]之间）
    • 标准化（把数据转化到均值为0，方差为1f范围内）
    • 缺失值（将缺失值处理成均值、中位数等）
  2. 类别型数据：
    • 降维（将多指标转化为少数几个综合指标）
    • PCA（降维的一种）
  3. 时间类型：
    • 时间的切分

归一化：

归一化首先在特征（维度）非常多的时候，可以防止某一维或某几维对数据影响过大，也是为了把不同来源的数据统一到一个参考区间下，这样比较起来才有意义，其次可以程序可以运行更快。

例如：一个人的身高和体重两个特征，假如体重50kg，身高175cm,由于两个单位不一样，数值大小不一样。如果比较两个人的体型差距时，那么身高的影响结果会比较大，因此在做计算之前需要先进行归一化操作。

归一化的公式为：

X'=(x−min)/(max​−min)
​​X" = X'*(mx-mi)+mi

其中max和min分别代表的是某列中的最大值和最小值，x为归一化之前的值。mx和mi为要归一化的区间，默认为[0,1]。

示例代码如下：

from sklearn.preprocessing import MinMaxScaler

def normalize():
  data = [
    [180,75,25],
    [175,80,19],
    [159,50,40],
    [160, 60, 32]
  ]
  scaler = MinMaxScaler(feature_range=(0,2))
  result = scaler.fit_transform(data)
  print(result)

归一化因为非常容易受到最大值和最小值的影响，因此如果数据集中存在一些异常点，结果将发生很大的改变，因此这种方法鲁棒性（稳定性）比较差，只适合数据量比较精确，比较小的情况。

标准化：

常用的方法是z-score标准化，经过处理后的数据均值为0，标准差为1，满足标准正太分布，标准正太分布如下：

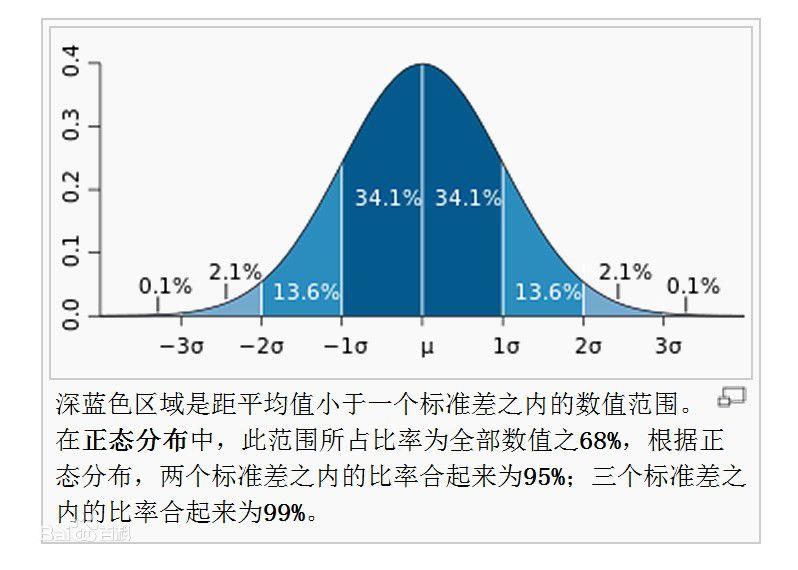
处理公式为：

X' = (x-μ)/σ

其中μ是样本的均值，σ是样本的标准差，它们可以通过现有的样本进行估计，在已有的样本足够多的情况下比较稳定，适合嘈杂的数据场景。

标准差的求法是先求方差，方差std的求法如下：

𝑠𝑡𝑑=((𝑥1−𝑚𝑒𝑎𝑛)^2+(𝑥2−𝑚𝑒𝑎𝑛)^2+…)/(𝑛(每个特征的样本数))

然后标准差𝜎则开根号：

𝜎=√std

方差和标准差越趋近于0，则表示数据越集中，如果越大，则表示数据越离散。

def standard():
  data = [
    [180, 75, 25],
    [175, 80, 19],
    [159, 50, 40],
    [160, 60, 32]
  ]
  scaler = StandardScaler()
  result = scaler.fit_transform(data)
  print(result)
  print("="*10) 
  print("="*10)
  print(scaler.var_)

缺失值处理：

缺失值一般有两种处理方式。第一种是直接进行删除，第二种是进行替换。除非缺失值占总数据集的比例非常少，才推荐使用删除的方式，否则建议使用“平均值”、“中位数”的方式进行替换。在scikit-learn中，有专门的缺失值处理方式，叫做sklearn.preprocessing.Imputer。

示例代码如下：

from sklearn.impute import SimpleImputer
def missing():
  im = SimpleImputer()
  data = im.fit_transform([
    [1,2],
    [np.NAN,4],
    [9,1]
  ])
  print(data)

特征选择和数据降维

一个数据集中可能会有以下问题：

  1. 冗余：部分特征的相关度高，容易消耗计算性能。
  2. 噪声：部分特征对预测结果有负影响。

因此就需要进行数据降维和特征选择。

特征选择：

特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征，特征在选择前和选择后可以改变值、也可以不改变值，但是选择后的特征维数肯定比选择前小，毕竟我们只选择了其中的一部分特征。

特征选择可以分为三种方式：

  1. Filter（过滤式）：VarianceThreshold。
  2. Embedded（嵌入式）：正则化、决策树。
  3. Wrapper（包裹式）：不常用。

过滤选择：

过滤式的特征选择是根据方差来的，他会删除所有低方差的特征。默认会删除所有方差为0的数据。可以使用sklearn.feature_selection.VarianceThreshold(threshold = 0.0)来实现过滤：

from sklearn.feature_selection import VarianceThreshold
from sklearn.preprocessing import StandardScaler

data = [
  [0, 2, 0, 3],
  [0, 1, 4, 3],
  [0, 1, 1, 3]
]

var = VarianceThreshold(threshold=2)
result = var.fit_transform(data)
print(result)

scaler = StandardScaler()
scaler.fit_transform(data)
print(scaler.var_)

因为方差越小，说明数据越集中，说明这个特征对于整个结果影响并不大，所以优先删除方差等于零或者接近0的特征。

PCA（主成分分析）：

主成分分析（Principal Component Analysis，PCA），是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

在用统计分析方法研究多变量的课题时，变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

主成分分析求解步骤：

1. 获取方差最大的正交变换：

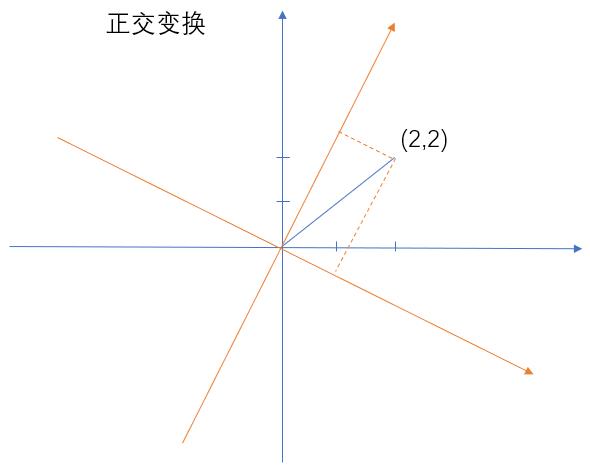
以上蓝色坐标轴是原来数据的坐标，经过变换后得到黄色的坐标，这样就可以将我们的数据变成另外一个值了。但是这个正交变换改怎么变？我们是通过方差来决定的，也就是变换完后，哪个方差最大，那么就选择哪个。

变换的公式如下：

[ p 1 p 2 . . . p r ] ∗ [ a 1 　 a 2 　 . . . 　 a m ] = [ p 1 a 1 　 p 1 a 2 　 . . . 　 p n a m p 2 a 1 　 p 2 a 2 　 . . . 　 p n a m . . . p r a 1 　 p r a 2 　 . . . 　 p r a m ] \\left[\\begin{matrix} p_1 \\\\ p_2 \\\\ ... \\\\ p_r \\end{matrix} \\right] * \\left[\\begin{matrix} a_1　a_2　...　a_m \\end{matrix} \\right] = \\left[\\begin{matrix} p_1a_1　p_1a_2　...　p_na_m \\\\ p_2a_1　p_2a_2　...　p_na_m \\\\ ... \\\\ p_ra_1　p_ra_2　...　p_ra_m \\end{matrix} \\right] ⎣⎢⎢⎡​p1​p2​...pr​​⎦⎥⎥⎤​∗[a1​　a2​　...　am​​]=⎣⎢⎢⎡​p1​a1​　p1​a2​　...　pn​am​p2​a1​　p2​a2​　...　pn​am​...pr​a1​　pr​a2​　...　pr​am​​⎦⎥⎥⎤​

2. 生成更多主成分：

以上是生成一个主成分（新的特征）的步骤。一般我们会生成多个主成分，但是生成多个主成分，必须要遵循一个条件，也就是多个主成分之间不能存在线性相关（特征之间可以通过某种公式来互转），用数学中的语言来表示则为协方差：

C o v ( F 1 , F 2 . . . , F n ) = 1 n ∑

以上是关于机器学习带你搞懂什么是特征工程？(特征抽取&特征预处理&特征选择&数据降维)的主要内容，如果未能解决你的问题，请参考以下文章

回炉重造带你搞懂什么是机器学习？

回炉重造带你搞懂什么是机器学习？

机器学习基础一文带你用sklearn做特征工程

机器学习 | 特征工程（数据预处理特征抽取）

以❤️简单易懂❤️的语言带你搞懂有监督学习算法附Python代码详解机器学习系列之KNN篇

机器学习基础