八大排序-上次看到这么好的排序博客还是在上次
Posted 吾仄lo咚锵
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了八大排序-上次看到这么好的排序博客还是在上次相关的知识,希望对你有一定的参考价值。

本文将用说人话+动图的形式带你搞懂常见排序算法,简要分析复杂度、稳定性等指标,并给出参考代码。最后安利sort()函数的使用。
选择排序
每次选择后面最小的元素放在前面。
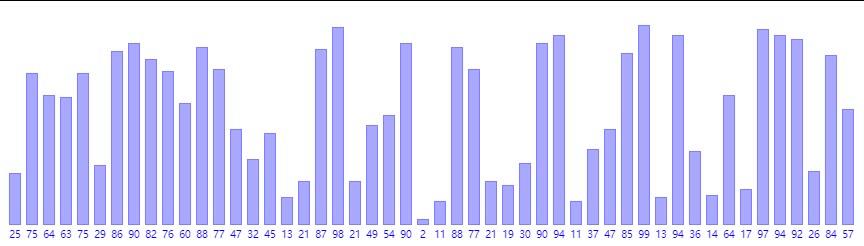
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 稳定性:不稳定
如2 2 1,第一趟选出最小的1后交换得到1 2 2,两个2相对位置改变。
稳定性:就是(关键字/元素值)相同的元素排序后的相对位置是否改变。
- 排序趟数是否与原序列有关:无关
无论升序乱序,选择排序每趟都要遍历到最后一个元素,才能确保选出的元素是最小的。
#include<bits/stdc++.h>
using namespace std;
void selection(int a[],int n){
for(int i=0;i<n;i++){
int min=i; //记录最小元素
for(int j=i+1;j<n;j++){ //找出后面最小元素
if(a[j]<a[min])
min=j;
}
swap(a[i],a[min]); //交换
}
}
int main(){
int a[5]={3,5,1,4,2};
selection(a,5);
for(int i=0;i<5;i++)cout<<a[i]<<" ";
return 0;
}
冒泡排序
从前往后比较两两相邻的元素,如果前者>后者,则交换它们。元素就像气泡一样往后冒。
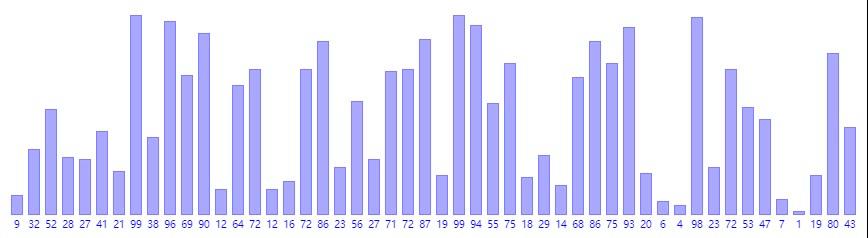
-
时间复杂度 O ( n 2 ) O(n^2) O(n2)
-
稳定性:稳定
遇到相同或更大元素时,不会交换。 -
排序趟数是否与原序列有关:有关
已经升序的极端条件下,可以记录是否发生交换,若无交换则序列有序,退出即可。
#include<bits/stdc++.h>
using namespace std;
void bubble(int a[],int n){
for(int i=0;i<n;i++){
bool tag=false; //记录此趟是否发生交换
for(int j=0;j<n-i-1;j++){//后面i个最大的已冒到顶了不用管(写成n问题也不大)
if(a[j]>a[j+1]){ //和后一个元素比较
swap(a[j],a[j+1]);
tag=true;
}
}
if(tag==false)break; //没有发生交换,退出
}
}
int main(){
int a[5]={3,5,1,4,2};
bubble(a,5);
for(int i=0;i<5;i++)cout<<a[i]<<" ";
return 0;
}
插入排序
每次将待排序的元素正确插入到前面已经排好序的序列中,就像理扑克牌一样。
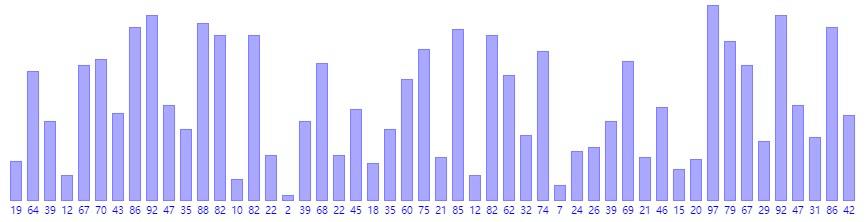
-
时间复杂度 O ( n 2 ) O(n^2) O(n2)
-
稳定性:稳定
从后向前先比较再移动,遇到相同不会交换。 -
排序趟数是否与原序列有关:无关
每趟插入1个元素,固定n-1趟。
#include<bits/stdc++.h>
using namespace std;
void insertion(int a[],int n){
for(int i=0;i<n;i++){ //遍历i个待插元素
for(int j=i;j>0;j--){ //插入前面
if(a[j]<a[j-1]) //小则交换
swap(a[j],a[j-1]);
else break; //否则已插入正确位置
//其实不break问题也不大,都是n方
}
}
}
int main(){
int a[5]={1,2,3,4,5};
insertion(a,5);
for(int i=0;i<5;i++)cout<<a[i]<<" ";
return 0;
}
希尔排序
每次把相隔x(增量)的元素划分成一个子表,进行直接插入排序(先不管其他元素),然后不断缩小x。从基本有序到整体有序。
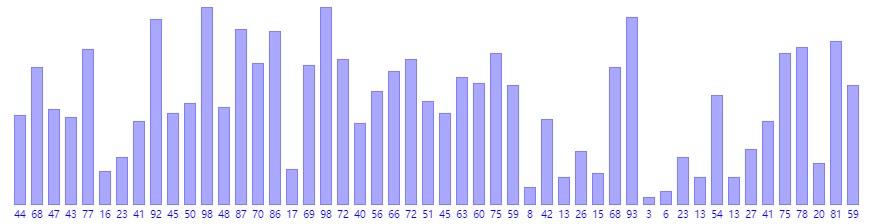
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 稳定性:不稳定
相同元素被划分到不同子表时,可能会改变它们的相对位置。 - 排序趟数是否与原序列有关:无关
无论原序列状态如何,都只与增量x(即数组大小n)有关。
#include<bits/stdc++.h>
using namespace std;
void shell(int a[],int n){
for(int x=n/2;x>0;x/=2){ //增量x
for(int i=x;i<n;i++){ //划分子表
//子表内插入排序
for(int j=i;j>=x&&a[j]<a[j-x];j-=x)
swap(a[j],a[j-x]);
}
}
}
int main(){
int a[5]={3,5,1,4,2};
shell(a,5);
for(int i=0;i<5;i++)cout<<a[i]<<" ";
return 0;
}
快速排序
每趟将比该元素大的放在它右边,比它小的放在它左边,那么该元素的位置就确定了,再递归的排序其他元素即可。
-
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
需要确定 n n n个数的正确位置,每趟最多比较次左右两半区间,复杂度是 O ( l o g n ) O(logn) O(logn)。 -
稳定性:不稳定
在交换左右两边的数时会改变相对位置。 -
排序趟数是否与原序列有关:有关
根据所选的数,来移动两边的数,使左小右大,在逆序的极端条件下,复杂度退化成 O ( n 2 ) O(n^2) O(n2)(每趟都要把右边的数全部移到左边)。
优化tip:选数不要默认选第一个数(cur=a[low]),可以随机,亦可以选头中尾三个数的中位数,使左右两半大小尽可能相等,从而减少移动次数。
快排YYDS,不少算法题也涉及快排思想。
#include<bits/stdc++.h>
using namespace std;
int partition(int a[],int low,int high){ //一趟划分
int cur=a[low]; //选第一个数来划分
while(low<high){
while(low<high&&a[high]>=cur)high--; //从后往前找比当前值小的元素
a[low]=a[high]; //把小的换到前面去
while(low<high&&a[low]<=cur)low++; //从前往后找比当前值大的元素
a[high]=a[low]; //把大的换到后面去
}
//当low=high,跳出循环,这个位置就是当前元素的正确位置了
a[low]=cur;
return low;
}
void qsort(int a[],int low,int high){
if(low<high){
int idx=partition(a,low,high); //确定该元素的正确位置
qsort(a,low,idx-1); //递归左右两个区间
qsort(a,idx+1,high);
}
}
int main(){
int a[5]={3,5,1,4,2};
qsort(a,0,4);
for(int i=0;i<5;i++)cout<<a[i]<<" ";
return 0;
}
(
插播反爬信息)博主CSDN地址:https://wzlodq.blog.csdn.net/
堆排序
以大根堆为例,即根元素是最大的。初始时无序,从下往上(叶节点往根)的方向,将两个叶子节点中值更大的元素和它的父节点交换,父节点换下来后如果还有子节点(即除了最后一层),则还要比较是否比现在的两个叶子节点更大,不然选更大的叶节点换上来,依次递归。

- 时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
n − 1 n-1 n−1次向下调整操作,每次调整复杂度是 O ( h ) O(h) O(h)即 O ( l o g n ) O(logn) O(logn)。 - 稳定性:不稳定
可能把后面相同的关键字调整到前面。 - 排序趟数是否与原序列有关:有关
如果有序,每次向下调整的复杂度是 O ( 1 ) O(1) O(1)。
适合频繁增删的场景,不必每次重新排序(虽然这里没给增删代码,偷懒)。
#include<bits/stdc++.h>
using namespace std;
void adjustheap(int a[], int i, int n){
for(int j=i*2+1;j<n;){
if(j+1<n&&a[j]<a[j+1]) //取左右孩子中较大的那个
j++;
if(a[i]>a[j])break;
swap(a[i], a[j]);
//交换后递归比较与子节点大小
i=j;
j=2*i+1;
}
}
void makeheap(int a[], int n){ //建堆
for(int i=n/2-1; i>=0; i--)//递归从最后一个父节点开始调整堆
adjustheap(a,i,n);
}
void heapsort(int a[], int n){
makeheap(a, n);
for(int i=n-1; i>=0; i--){
swap(a[i], a[0]);
adjustheap(a, 0, i);
}
}
int main(){
int a[5]={3,5,1,4,2};
heapsort(a,5);
for(int i=0;i<5;i++)cout<<a[i]<<" ";
return 0;
}
归并排序
递归的划分子区间直到一个元素,然后依次合并子区间,此时每个子区间内部有序。合并过程就是比较两个子区间的最前面元素,取最小的那个,直到一个子区间取完了,那么再直接加上另一个子区间剩下元素即可。
- 时间复杂度
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
每趟归并 O ( n ) O(n) O(n),共需要 O ( l o g n ) O(logn) O(logn)趟归并。 - 稳定性:稳定
归并操作从前往后合并两个子区间,不会改变相对位置。 - 排序趟数是否与原序列有关:无关
无论原序列状态如何,都要划分到一个元素然后开始归并。
求逆序对的老常客了,还有可以应用排序超大文件(eg:内存2G,硬盘2T的文件数据,问你怎么排序)。
#include<bits/stdc++.h>
using namespace std;
int b[5]; //辅助数组
void merge(int a[],int low,int mid,int high){
for(int k=low;k<=high;k++)b[k]=a[k];
int i=low,j=mid+1,k=low;
//i,j分别表示左右子区间最前面元素下标
//k表示合并后数组下标
while(i<=mid&&j<=high){
if(b[i]<=b[j])
a[k++]=b[i++];
else a[k++]=b[j++];
}
while(i<=mid)a[k++]=b[i++];
while(j<=high)a[k++]=b[j++];
}
void mergeSort(int a[],int low,int high){
if(low<high){
int mid=(low+high)/2; //从中间划分区间
mergeSort(a,low,mid); //分别归并左右区间
mergeSort(a,mid+1,high);
merge(a,low,mid,high); //归并
}
}
int main(){
int a[5]={3,5,1,4,2