数据挖掘笔记分类

Posted 2021-11-22 YWP_2016

理论

• Hunt算法是许多决策树算法的基础，包括ID3、C4.5和CART
• 增益率（gain ratio）：如决策树算法C4.5，采用增益率的划分标准来评估划分
• 树剪枝tree-pruning：决策树过大容易过拟合overfitting，通过树剪枝（修剪初始决策树的分支），减小决策树的规模，提高决策树的泛化能力
• 分类模型的误差：训练误差（training error）、泛化误差（generalization error）。一个好的分类模型不仅要能够很好地拟合训练数据，还需对未知样本进行准确的分类。
• 注意：决策树很小时，训练和检验误差都很大——模型拟合不足（model underfitting），这是因为模型尚未学习到数据的真实结构。随着决策树中结点数增加，训练和检验误差都降低。然而，一旦树的规模太大，即使训练误差还在继续降低，但检验误差开始增大——模型过分拟合（model overfitting）。
• 奥卡姆剃刀：给定两个具有相同泛化误差的模型，较简单的模型比较复杂的模型更可取。
• 交叉验证：二折交叉验证：数据分为两个相同大小的子集，首先选择其一作为训练集，另一个作为检验集，然后交换两个集合的角色。k二折交叉验证：数据分为k个相同大小的子集，选择其一作为检验集，其余全作为训练集，重复k次，使得每份数据都用于检验恰好一次。
• k二折交叉验证的特殊情况：留一leave out方法：k=N（数据集大小）

理论+实践

基于规则的分类器

• 分类规则质量的度量指标：覆盖率coverage、准确率accuracy

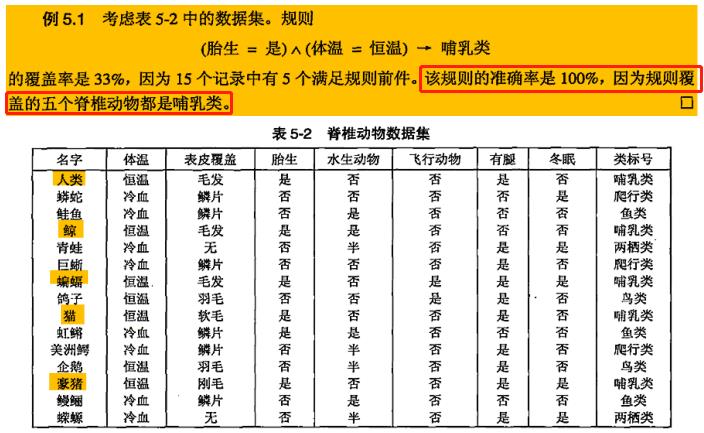
•  基于规则的分类器所产生的的规则集的两个重要性质：互斥规则（不存在两条规则被同一记录出发，即规则是互斥的）、穷举规则（每条记录都至少被一条规则覆盖）→→→保证每条记录被且仅被一条规则覆盖。
• 提取分类规则的方法：直接方法（直接从数据中提取分类规则）、间接方法（从其他分类模型（如决策树和神经网络）提取分类规则）。【原则上，决策树从根节点到叶结点的每条路径=都可表示为一条分类规则】

最近邻分类

• 样例z的k-最近邻：与z距离最近的k个数据点

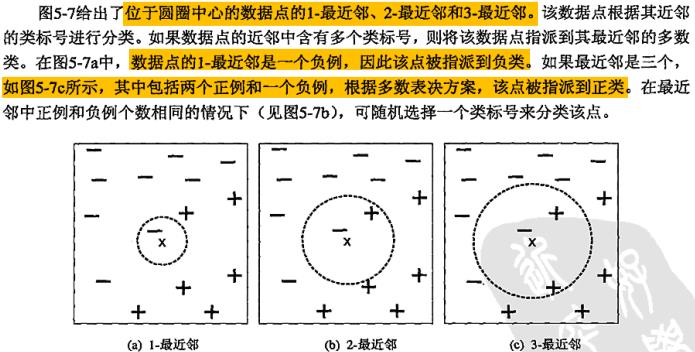
• 最近邻分类器基于局部信息预测，而决策树与基于规则的分类器试图找到一个拟合整个输入空间的全局模型。正是因为这样的局部分类决策，最近邻分类器（k很小时）对噪声非常敏感。
• 最近邻分类器可以生成任意形状的决策边界，与决策树与基于规则的分类器通常所局限的直线决策边界相比，能够提供更灵活的模型表示。

 决策树分类

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from matplotlib.font_manager import FontProperties
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
plt.show()
plt.rcParams['font.sans-serif']=['SimHei']

############获取数据############
iris_data = datasets.load_iris()
X = iris_data.data[:, [2, 3]]
y = iris_data.target
label_list = ['山鸢尾', '杂色鸢尾', '维吉尼亚鸢尾']

############构建决策边界############
def plot_decision_regions(X, y, classifier=None):
    marker_list = ['o', 'x', 's']
    color_list = ['r', 'b', 'g']
    cmap = ListedColormap(color_list[:len(np.unique(y))]) # 背景色

    # 生成网格点坐标矩阵
    x1_min, x1_max = X[:, 0].min()-1, X[:, 0].max()+1
    x2_min, x2_max = X[:, 1].min()-1, X[:, 1].max()+1
    t1 = np.linspace(x1_min, x1_max, 666)
    t2 = np.linspace(x2_min, x2_max, 666)
    x1, x2 = np.meshgrid(t1, t2) # 生成网格点坐标矩阵
    y_hat = classifier.predict(np.array([x1.ravel(), x2.ravel()]).T)
    y_hat = y_hat.reshape(x1.shape)
    plt.contourf(x1, x2, y_hat, alpha=0.2, cmap=cmap)   # 绘制轮廓等高线  alpha参数设置透明度
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)

    # plot class samples
    for ind, clas in enumerate(np.unique(y)):
        plt.scatter(X[y == clas, 0], X[y == clas, 1], alpha=0.8, s=50,
                    c=color_list[ind], marker=marker_list[ind], label=label_list[clas])


############训练模型############
tree = DecisionTreeClassifier(criterion='gini', max_depth=5, random_state=1)
tree.fit(X, y)

############可视化############
plot_decision_regions(X, y, classifier=tree)
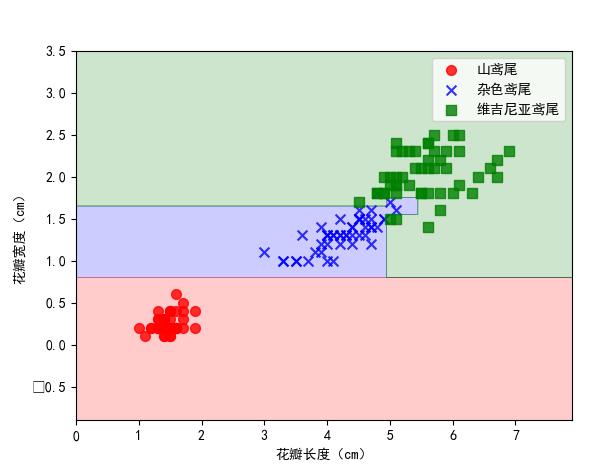
plt.xlabel('花瓣长度（cm）')
plt.ylabel('花瓣宽度（cm）')
plt.legend()
plt.show()

鸢尾花数据集 决策树分类

贝叶斯分类

• 对属性集和类变量的概率关系建模 

朴素贝叶斯分类器

• 估计类条件概率时，假设属性之间条件独立：如果P(X,Y|Z)=P(X|Z)P(Y|Z)，或等价地P(X|Y,Z）=P(X|Z），则称事件X,Y对于给定事件Z是条件独立的，也就是说，当Z发生时，X发生与否与Y发生与否是无关的。

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB, GaussianNB
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from matplotlib.font_manager import FontProperties
import numpy as np
import matplotlib as mpl
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
plt.rcParams['font.sans-serif']=['SimHei']

############获取数据############
iris_data = datasets.load_iris()
X = iris_data.data[:, :2]
y = iris_data.target
label_list = ['山鸢尾', '杂色鸢尾', '维吉尼亚鸢尾']


############构建决策边界############
def plot_decision_regions(X, y, classifier=None):
        marker_list = ['o', 'x', 's']
        color_list = ['r', 'b', 'g']
        cmap = ListedColormap(color_list[:len(np.unique(y))])  # 背景色

        # 生成网格点坐标矩阵
        x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
        x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
        t1 = np.linspace(x1_min, x1_max, 666)
        t2 = np.linspace(x2_min, x2_max, 666)
        x1, x2 = np.meshgrid(t1, t2)  # 生成网格点坐标矩阵
        y_hat = classifier.predict(np.array([x1.ravel(), x2.ravel()]).T)
        y_hat = y_hat.reshape(x1.shape)
        plt.contourf(x1, x2, y_hat, alpha=0.2, cmap=cmap)  # 绘制轮廓等高线  alpha参数设置透明度
        plt.xlim(x1_min, x1_max)
        plt.ylim(x2_min, x2_max)

        # plot class samples
        for ind, clas in enumerate(np.unique(y)):
                plt.scatter(X[y == clas, 0], X[y == clas, 1], alpha=0.8, s=50,
                            c=color_list[ind], marker=marker_list[ind], label=label_list[clas])


############训练模型############
clf = Pipeline([
         ('sc', StandardScaler()),
         ('clf', GaussianNB())])
ir = clf.fit(X, y.ravel()) # 利用训练数据进行拟合

############可视化############
plot_decision_regions(X, y, classifier=clf)
plt.xlabel('花萼长度（cm）')
plt.ylabel('花萼宽度（cm）')
plt.legend()
plt.show()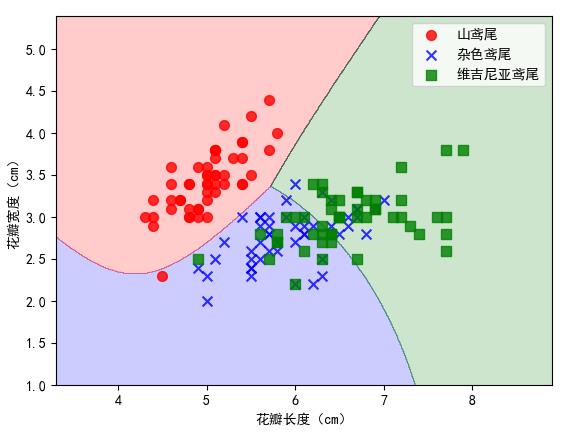

贝叶斯信念网络

• Bayesian belief networks, BBN 贝叶斯网络：不要求给定类的所有属性都条件独立，而是允许指定哪些属性条件独立
• 因数据和先验知识以概率方式相结合，故该方法对模型的过拟合是非常鲁棒的

人工神经网络

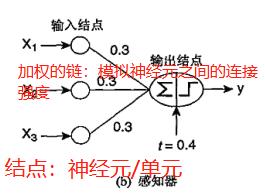
• 感知器Perceptron：对输入加权求和，减去偏置因子，然后考察结果的符号→→得到输出值y。训练：不断调整权值参数w，直到输出和训练样例的实际输出一致。

 

 

文献阅读

赵秦怡,王丽珍,罗桂兰.基于co-location模式的空间分类算法[J].计算机应用与软件,2018,35(03):225-229.

• 背景：在特定的空间分类任务中，对象的类别和自身属性相关较小，和近邻对象的空间特征相关较大，传统的空间分类方法并不适用。

• 方法：提出一种基于co-location模式的空间分类挖掘算法。算法挖掘含不同类别特征的空间co-location模式，转化为分类规则，获得兴趣度较高的分类规则集。分类阶段先查询待分类对象的空间近邻，概化为空间特征，挑选适应的分类规则进行分类。

• 结果：实验结果表明这是一种高效的空间分类算法。