支持向量机，核函数映射，高斯函数，对偶优化

Posted 2021-11-22 ZhangJiQun.

目录

支持向量机

为何叫支持向量机

支持向量

线性可分

1.2 最大间隔超平面

1.3 支持向量

1.4 SVM 最优化问题

ModuleNotFoundError: No module named 'sklearn.datasets.samples_generator'

如何处理线性不可分

核函数映射示例

高斯核函数

对偶问题

---

支持向量机

是用来解决分类问题的。

假设决定他们分类的有两个属性，花瓣尺寸和颜色。单独用一个属性来分类，像刚才分米粒那样，就不行了。这个时候我们设置两个值 尺寸x和颜色y.

我们把所有的数据都丢到x-y平面上作为点，按道理如果只有这两个属性决定了两个品种，数据肯定会按两类聚集在这个二维平面上。

我们只要找到一条直线，把这两类划分开来，分类就很容易了，以后遇到一个数据，就丢进这个平面，看在直线的哪一边，就是哪一类。

比如x+y-2=0这条直线，我们把数据(x,y)代入，只要认为x+y-2>0的就是A类，x+y-2<0的就是B类。

以此类推，还有三维的，四维的，N维的 属性的分类，这样构造的也许就不是直线，而是平面，超平面。

一个三维的函数分类 ：x+y+z-2=0，这就是个分类的平面了。

有时候，分类的那条线不一定是直线，还有可能是曲线，我们通过某些函数来转换，就可以转化成刚才的哪种多维的分类问题，这个就是核函数的思想。

例如：分类的函数是个圆形x^2+y^2-4=0。这个时候令x^2=a; y^2=b,还不就变成了a+b-4=0 这种直线问题了。

这就是支持向量机的思想。

机的意思就是 算法，机器学习领域里面常常用“机”这个字表示算法

支持向量意思就是 数据集种的某些点，位置比较特殊，比如刚才提到的x+y-2=0这条直线，直线上面区域x+y-2>0的全是A类，下面的x+y-2<0的全是B类，我们找这条直线的时候，一般就看聚集在一起的两类数据，他们各自的最边缘位置的点，也就是最靠近划分直线的那几个点，而其他点对这条直线的最终位置的确定起不了作用，所以我姑且叫这些点叫“支持点”（意思就是有用的点），但是在数学上，没这种说法，数学里的点，又可以叫向量，比如二维点(x,y)就是二维向量，三维度的就是三维向量（ x,y,z)。所以 “支持点”改叫“支持向量”

• 1.SVM原始模型构建
• 2.对偶形式的推导
• 3.求解的方法
• 4.软间隔SVM及核方法
• 5.SVM优缺点及应用

支持向量机(Support Vector Machine,SVM)，二类分类器，它最终能告诉你一个东西是属于A还是属于B。在由样本点构成的向量空间内，SVM通过找到一个可以将两类数据正确分隔在两侧的划分超平面，达到对数据分类及预测的效果。而这个超平面是通过支持向量确定的，机的意思呢就是算法，故支持向量机就是通过支持向量确定划分超平面，从而做到分类及预测的算法。

为何叫支持向量机

之所以叫支持向量机，因为其核心理念是：支持向量样本会对识别的问题起关键性作用。那什么是支持向量（Support vector）呢？支持向量也就是离分类超平面（Hyper plane）最近的样本点。

有两类样本数据（红色和蓝色的小圆点），中间的蓝线是分类超平面，两条边缘上的点（2个蓝线蓝色和1个蓝线红心）是距离超平面最近的点，这些点即为支持向量。简单地说，作为支持向量的样本点非常非常重要，以至于其他的样本点可以视而不见。而这个分类超平面正是SVM分类器，通过这个分类超平面实现对样本数据一分为二。

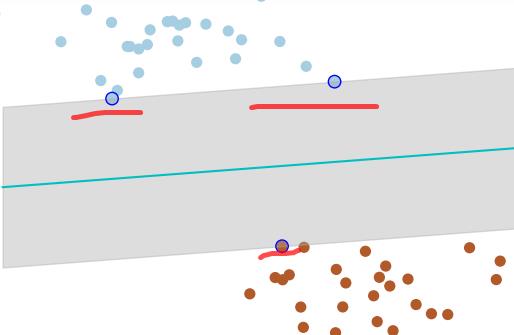
支持向量

线性可分

首先我们先来了解下什么是线性可分。

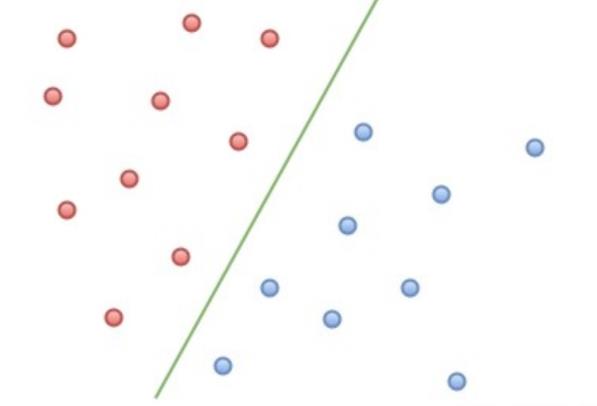
在二维空间上，两类点被一条直线完全分开叫做线性可分。

1.2 最大间隔超平面

什么是超平面？
-超平面是指 n 维线性空间中维度为 n-1 的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块。
在样本空间中，划分超平面可通过线性方程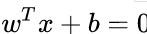来描述，其中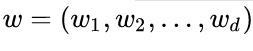为法向量，决定超平面的方向；为位移项，决定超平面与原点之间的距离。一个划分超平面就由法向量和位移确定。

• 两类样本分别分割在该超平面的两侧；
• 两侧距离超平面最近的样本点到超平面的距离被最大化了。

1.3 支持向量

 

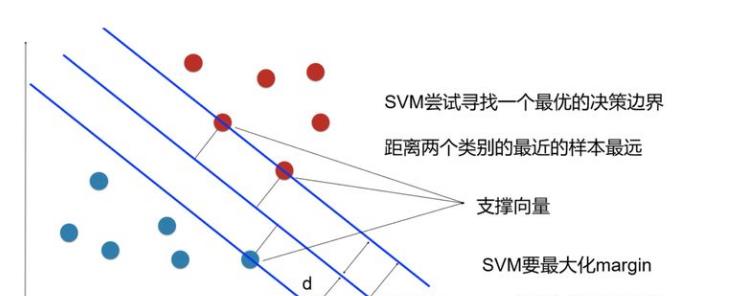
样本中距离超平面最近的一些点，这些点叫做支持向量。

1.4 SVM 最优化问题

SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：

 

 

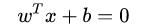
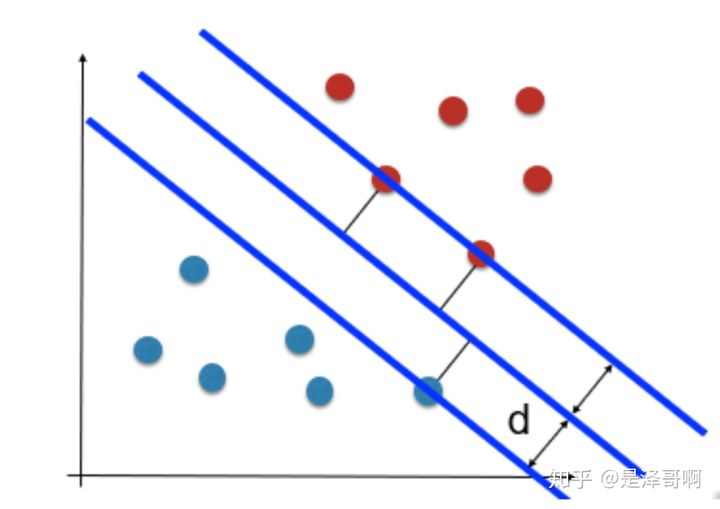
如图所示，根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d。

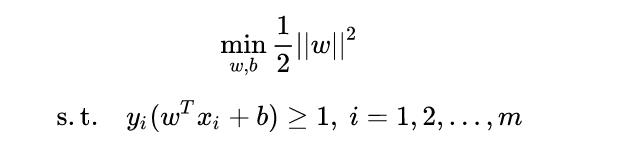
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.svm import SVC
 
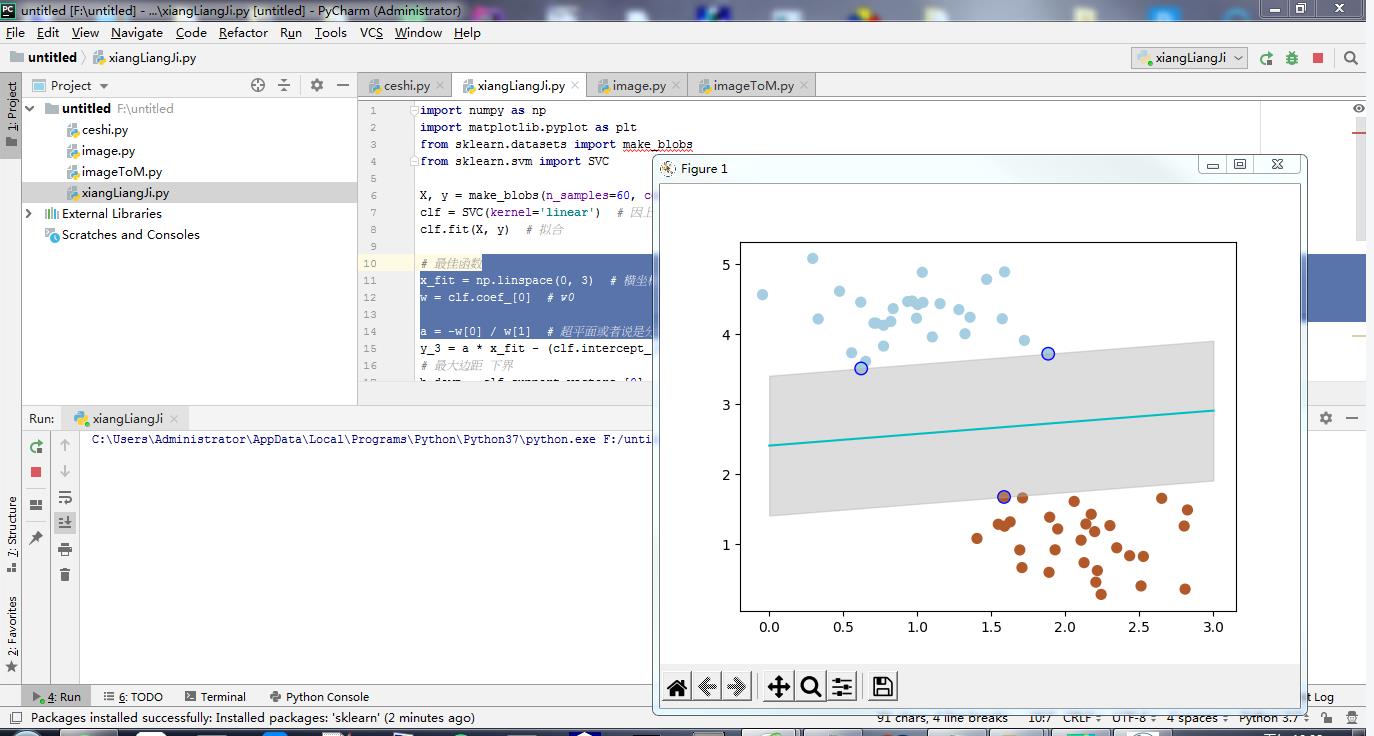
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4) # 生成实验数据
clf = SVC(kernel='linear') # 因上一行中centers=2，作为一个二分类问题我们选择使用linear作为核函数
clf.fit(X, y) # 拟合
 
# 最佳函数
x_fit = np.linspace(0, 3) # 横坐标
w = clf.coef_[0] # w0
 
a = -w[0] / w[1] # 超平面或者说是分类线的斜率
y_3 = a * x_fit - (clf.intercept_[0]) / w[1] # 超平面方程
# 最大边距 下界
b_down = clf.support_vectors_[0]
y_down = a * x_fit + b_down[1] - a * b_down[0]
# 最大边距 上界
b_up = clf.support_vectors_[-1]
y_up = a * x_fit + b_up[1] - a * b_up[0]
 
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b', s=80, facecolors='none')
plt.show()

ModuleNotFoundError: No module named 'sklearn.datasets.samples_generator'

直接从sklearn.datasets中导入make_blobs
将from sklearn.datasets.samples_generator import make_blobs修改为：
from sklearn.datasets import make_blobs

如何处理线性不可分

统的SVM 要求样本数据是线性可分的，这样才会存在分类超平面。而如果样本数据是非线性的情况，那将如何处理呢？SVM的解决办法就是先将数据变成线性可分的，再构造出最优分类超平面。

SVM 通过选择一个核函数 K ，将低维非线性数据映射到高维空间中。原始空间中的非线性数据经过核函数映射转换后，在高维空间中变成线性可分的数据，从而可以构造出最优分类超平面。

如下图所示：原始样本数据在二维空间里无法线性分割，经过核函数映射到三维空间中则可构造出分类超平面进行二类划分。

 

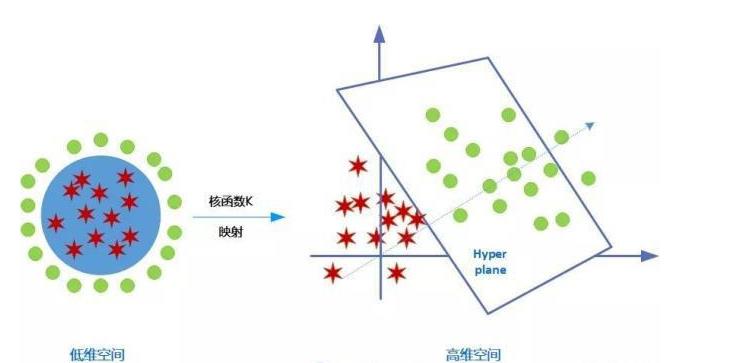
核函数映射示例

简单地说，核函数是计算两个向量在隐式映射后空间中的内积的函数。核函数通过先对特征向量做内积，然后用函数 K 进行变换，这有利于避开直接在高维空间中计算，大大简化问题求解。并且这等价于先对向量做核映射然后再做内积。

在实际应用中，通常会根据问题和数据的不同，选择不同的核函数。例如，常用的有以下几种：

线性核函数，就是简单原始空间中的内积。

多项式核函数，可根据R和d的取值不同，而有不同的计算式。

高斯核函数

可根据实际需要灵活选取参数σ，甚至还可以将原始维度空间映射到无穷维度空间。不过，如果σ取值很大，会导致高次特征上的权重衰减快；如果σ取值很小，其好处是可以将任意的数据映射成为线性可分，但容易造成过拟合现象。

高斯核函数是非常经典，也是使用最广泛的核函数之一。下图是把低维线性不可分的数据通过高斯核函数映射到了高维空间的示例图：

 

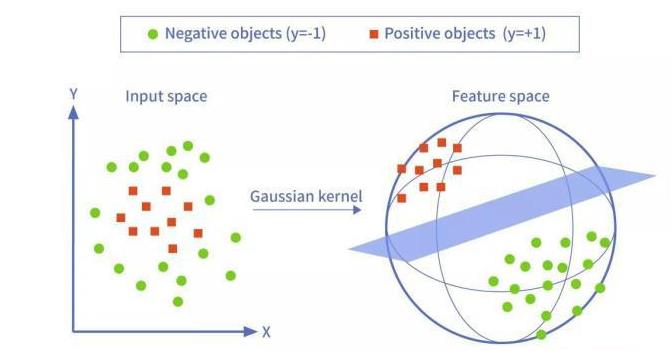
至此，我们已经知道核函数不使用显式的计算核映射，并且能够很好地解决线性不可分问题。在实际应用中，如果训练样本数量大，经训练后得出的模型中支持向量的数量会有很多，利用该模型进行新样本预测时，需要先计算新样本与每个支持向量的内积，然后做函数 K转换，耗时长、速度慢。

【机器学习】支持向量机 SVM（非常详细） - 知乎

对偶问题

首先顺带一提，上面的基本型是一个凸二次规划问题，可以直接用现成的优化计算包求解。但若利用“对偶问题”来求解会更高效，所以我们来推导SVM的对偶形式。

-什么是凸优化问题？
-直观来说就是在定义于凸集中的凸函数上求最小值。但需要注意的是，国内关于函数凹凸性的定义和国外是相反的，这里的凸函数是指开口向上的。由凸集和凸函数的定义可得出，凸优化问题具有一个极好的性质，即局部最优值必定是全局最优值，因为它不管是局部还是全局都只有那一个最优值。（实际上这个性质叫做强对偶性，且需满足一定的条件才能具备，我这里为了方便理解讲得比较牵强，想具体了解的可点开链接）
-什么是二次规划问题？
-如果一个问题的目标函数是变量的二次函数，约束条件是变量的线性函数，我们将其称为二次规划问题。