2021-2022-1 ACM集训队每周程序设计竞赛 - 问题 F: 逃离 - 题解
Posted Tisfy
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2021-2022-1 ACM集训队每周程序设计竞赛 - 问题 F: 逃离 - 题解相关的知识，希望对你有一定的参考价值。
逃离
时间限制：20秒
空间限制：128M
题目描述
取经成功的斗战胜佛又犯了事，这次他召唤了很多分身来逃离如来佛主的五指山。
悟空召唤了 N − 1 N-1 N−1个分身（加上真身，共有 N N N个孙猴子），每个猴子只能朝固定的一个方向移动，移动速度相同。
如来佛想要一掌压住所有的猴子，问你佛主的手掌的最小面积是多少。
为了简化问题，我们把天庭想象成一个二维坐标平面。
初始时，每个猴子都具有一个坐标和一个逃离方向：
U代表向上逃，即 y y y轴的正方向D代表向下逃，即 y y y轴的负方向L代表向左逃，即 x x x轴的负方向R代表向右逃，即 x x x轴的正方向
如来佛主的手掌想象成一个矩形，要压住所有的猴子，即某时刻所有的猴子都在矩形之内（或边界上）
输入描述
第一行一个正整数 N N N，代表共有 N N N只猴子
接下来 N N N行，每行有空格隔开的两个正整数和一个字符，分别代表这只猴子初始位置的 x x x、 y y y坐标及其逃离方向。
输入格式如下：
N
x1 y1 d1
x2 y2 d2
...
xn yn dn
其中：
- 1 ≤ N ≤ 1 0 5 1\\leq N\\leq10^5 1≤N≤105
- − 1 0 8 ≤ x i , y i ≤ 1 0 8 -10^8\\leq x_i, y_i\\leq 10^8 −108≤xi,yi≤108
- d i d_i di是 U U U, D D D, L L L 或 R R R。
输出描述
输出如来佛手掌的最小面积，答案保留6位小数。
样例一
输入
2
0 3 D
3 0 L
输出
0.000000
样例二
输入
5
-7 -10 U
7 -6 U
-8 7 D
-3 3 D
0 -6 R
输出
97.500000
提示
为了简化计算，如来佛的手掌只能是横着的矩形
题目即求整个过程中， ( x m a x − x m i n ) × ( y m a x − y m i n ) (x_{max}−x_{min})×(y_{max}−y_{min}) (xmax−xmin)×(ymax−ymin)的最小值。
样例一中，
两只猴子会在
(
0
,
0
)
(0,0)
(0,0)处相遇，此时盖猴儿所需手掌的面积为0
题目分析
这道题主要有两种做法。一个是三分，一个是取特殊值。
取特殊值
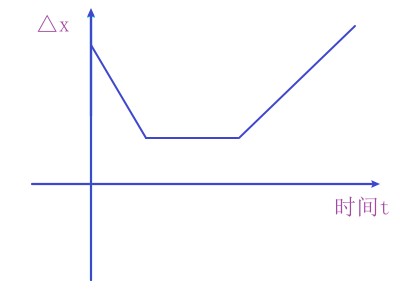
只针对一个方向（比如水平方向），讨论最左边的猴子和最右边的猴子的距离（即为 x m a x − x m i n x_{max}−x_{min} xmax−xmin），记为 Δ x \\Delta x Δx。
刚开始 Δ x \\Delta x Δx会减小一段时间（可能是0），之后 Δ x \\Delta x Δx会保持不变一段时间（可能是0），最后增大（可能是0）。
但 Δ x \\Delta x Δx的值变化趋势必是先减然后不变最后变大。
因此， Δ x \\Delta x Δx随着时间的变化而变化的函数如图所示：
比较重要的时刻也就4个端点。同理，竖直方向的最大距离 Δ y \\Delta y Δy的变化趋势也如上图所示。
先讨论 Δ x \\Delta x Δx和 Δ y \\Delta y Δy同时减小的部分，此时 Δ x × Δ y \\Delta x\\times\\Delta y Δx×Δy的值一定是逐渐变小的。
同理 Δ x \\Delta x Δx和 Δ y \\Delta y Δy同时增加的部分，此时 Δ x × Δ y \\Delta x\\times\\Delta y Δx×Δy的值一定是逐渐增大的。
这两种情况下，矩形面积的最小值一定在直线端点处。现在我们讨论 Δ x \\Delta x Δx和 Δ y \\Delta y Δy一个增加一个减少的情况。不失一般性，假设 Δ x \\Delta x Δx在减小而 Δ y \\Delta y Δy在增加。
如果 Δ x \\Delta x Δx减小的速率比 Δ y \\Delta y Δy增加的速率快，那么矩形的面积就不断减小。反之，若减小速率比增加速率慢，矩形面积就不断增加。
此时 Δ x × Δ y \\Delta x\\times \\Delta y Δx×Δy取最小值的时刻也是线段的断点处。
我们也可以写出 Δ x × Δ y \\Delta x\\times \\Delta y Δx×Δy的函数来得到 Δ x × Δ y \\Delta x\\times \\Delta y Δx×Δy的最小值。
总之，我们可以直接枚举所有 Δ x \\Delta x Δx的变化速率发生改变的时刻以及 Δ y \\Delta y Δy的变化速率发生改变的时刻，答案就在其中某个时刻。
Tips：
其实不管分身再多，很多猴子对答案都是没有影响的。我们只需要考虑几只特殊的猴子。
水平方向上，我们只需要考虑 4 4 4只猴子：
- 最左边的往左逃的猴子
- 最左边的往右逃的猴子
- 最右边的往左逃的猴子
- 最右边的往右逃的猴子
其他的猴子都始终在这4只猴子之内，就无需考虑了。
但此题时间限制较长，不优化也能在
10
10
10秒之内通过。
再加上竖直方向上的4只猴子，一共8只，能在几十毫秒内通过。
三分
如果不想像上述那样判断特殊时刻，我们也可以无脑三分。
简单讲述一下三分的思路：
对于一个 [ l , r ] [l,r] [l,r]上的凹函数，我们要求其最小值，可以每次在 [ l , r ] [l,r] [l,r]的两个三等分点处计算函数值，从而每次把函数的最小值逼近为原区间的 2 3 \\frac{2}{3} 32。
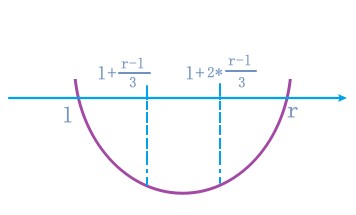
如图所示，我们要求凹函数在 [ l , r ] [l,r] [l,r]上的最小值，每次只需要先求出点 l + r − l 3 l+\\frac{r-l}{3} l+3r−l处的函数值和点 l + 2 × r − l 3 l+2\\times\\frac{r-l}{3} l+2×3r−l的函数值。
如果点
l
+
r
−
l
3
l+\\frac{r-l}{3}
l+3r−l处的函数值比点
l
+
2
×
r
−
l
3
l+2\\times\\frac{r-l}{3}
l+2×3r−l的函数值更大，说明函数最小值在
l
+
r
−
l
3
l+\\frac{r-l}{3}
l+3r−l和
r
r
r之间。否则说明在
l
l
l和
l
+
2
×
r
−
l
3
l+2\\times\\frac{r-l}{3}
l+2×3r−l之间。
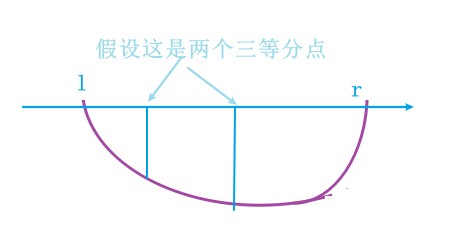
因此，我们每次更新 l l l或者 r r r的值，最小值所在区间就会变为原来的 2 3 \\frac{2}{3} 32。
假如初始区间长度为 r − l r-l r−l，那么经过 k k k次三分后，区间长度就会变为 ( r − l ) × ( 2 3 ) k (r-l)\\times(\\frac{2}{3})^k (r−l)×(32)k
我们只需要进行一定次数的三分即可。比如进行 300 300 300次三分，最小值区间就会变为原来的 ( 2 3 ) 300 ≈ 1.488 × 1 0 − 53 (\\frac{2}{3})^{300}\\approx1.488\\times10^{-53} (以上是关于2021-2022-1 ACM集训队每周程序设计竞赛 - 问题 F: 逃离 - 题解的主要内容，如果未能解决你的问题，请参考以下文章
BUCT - 2021-2022-1 ACM集训队每周程序设计竞赛（10）题解
BUCT - 2021-2022-1 ACM集训队每周程序设计竞赛题解
BUCT - 2021-2022-1 ACM集训队每周程序设计竞赛题解