打卡算法 12整数转罗马数字算法解析

Posted 2021-11-22 恬静的小魔龙

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了打卡算法 12整数转罗马数字算法解析相关的知识，希望对你有一定的参考价值。

推荐阅读

CSDN主页
GitHub开源地址
Unity3D插件分享
简书地址
我的个人博客
QQ群：1040082875

大家好，我是小魔龙，Unity3D软件工程师，VR、AR，虚拟仿真方向，不定时更新软件开发技巧，生活感悟，觉得有用记得一键三连哦。

一、题目

1、算法题目

“将输入的整数转化成罗马数字。”

题目链接：
来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/integer-to-roman/

2、题目描述

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
给你一个整数，将其转为罗马数字。

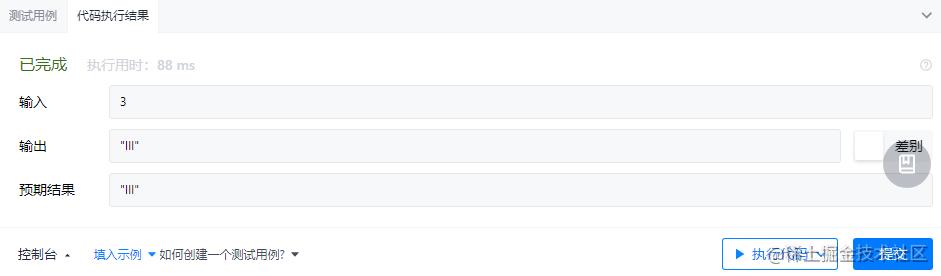
示例 1：
输入：num = 3
输出："III"

示例 2：
输入：num = 48
输出："XLVIII"
解析: XL = 40 , V = 5 , III = 3

示例 3：
输入：num = 4994
输出："MIVCMXCIV"
解析：MIV = 4000 , CM = 900 , XC = 90 , IV = 4

二、解题

1、思路分析

罗马数字由7个符号组成，每个符号对应一个具体的数值，根据减法规则给出了额外的6个复合符号，一共13个独特符号，如下图所示：

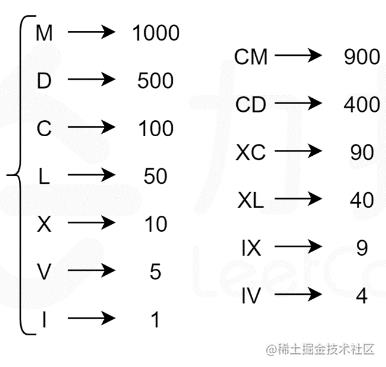
这道题的关键是整数转成罗马数字的时候选择尽可能大的符号值，比如140，最大可以选择符号值C = 100，然后 40 选择最大符号值 XL = 40。

2、代码实现

暴力解法：

这个思路相对比较简单，因为整数转罗马数字，每个位数上的数字都可以单独处理，使用模运算和触发运算，可以得到每个位上的数字，然后跟罗马数字中的数字对应起来组合即可。

public class Solution 
{
    public string IntToRoman(int num) 
    {
        string[] M = { "", "M", "MM", "MMM" }; // 1000，2000，3000
        string[] C = { "", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM" }; // 100~900
        string[] X = { "", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC" }; // 10~90
        string[] I = { "", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX" }; // 1~9
        return M[num / 1000] + C[(num % 1000) / 100] + X[(num % 100) / 10] + I[num % 10];
    }
}

贪心算法

贪心法则：每次尽量使用最大的数来表示，比如2118这个数，每次尽量选择最大的数来表示，那么就是 2000 ，100 ，10 ，8，会得到正确结果： MMCXVIII。

public class Solution 
{
    public string IntToRoman(int num) 
    {
        int[] values = { 1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1 };
        string[] rom = { "M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I" };
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < values.Length; i++)
        {
            while (num >= values[i])
            {
                sb.Append(rom[i]);
                num -= values[i];
            }
        }
        return sb.ToString();
    }
}