竞赛最好用的平衡树-Size Balanced Tree（SBT）建议收藏

Posted 2021-11-22 飞人01_01

大家好。

前段时间我更新过AVL、红黑树以及搜索二叉树的简单讲解。今天我们还是围绕着平衡树的话题，来讲解一个很牛逼的平衡树结构。这种结构是我国的一位大牛：陈启峰。在2006年，他还在读高中阶段，所发明的一种平衡树结构，叫Size Balanced Tree（SBT），根据节点的个数，来调整平衡性。一直到今天，这种平衡树结构，在算法竞赛领域是非常常用的，虽然SBT的时间复杂度跟AVL、红黑树这些平衡树一样，但是SBT是比较好写，比较好改的。所以在算法竞赛时，是最常用的一种算法。陈启峰SBT论文（译）

本期文章源码：GitHub

前期文章：

二叉树的概念以及搜索二叉树

AVL平衡树

浅析红黑树

文章目录

• 一、左右旋转
• 二、Maintain方法
• 三、add方法和delete方法

一、左右旋转

还是老样子，为了维持平衡性，SBT也是需要进行旋转操作的。只是说，调用旋转操作的时机，跟其他的平衡树有点区别而已。讲解旋转之前，我们先来认识SBT的节点：

//可以直接改为泛型，这里为了理解这种结构，就忽略了
public class SBTNode {
    public int val; //值域
    public SBTNode left, right; //左右孩子
    public int size; //节点数
    
    public SBTNode(int val) {
        this.val = val;
        size = 1; //默认节点大小是1
    }
}

SBT的节点，只是多了一个size域，用于表示以当前节点为根节点时，这颗子树的节点数。整棵树的平衡性，就是根据这个size来调整的。

右旋转：(LL型)

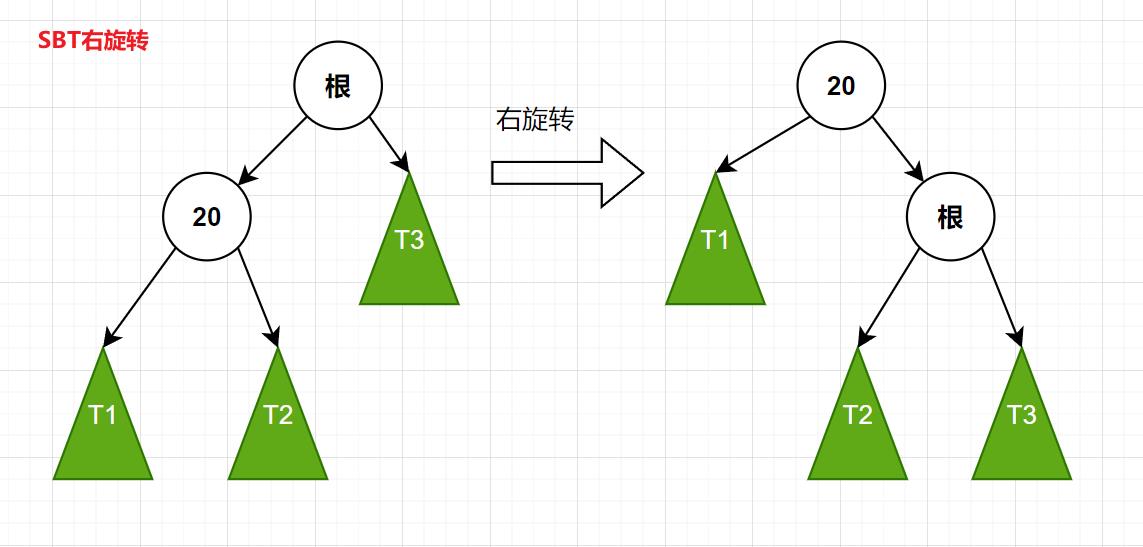
旋转操作的指针，相互之间的转换，我相信以前了解过平衡树的同学，应该是知道的（如果不知道，请翻阅前期文章）。问题就在于如何，如何修改这些节点的size？

看上图，T1-T3，表示子树，另外两个表示节点，旋转之后，我们会发现，T1和T2和T3这三颗子树，他们下面的节点是没有发生改变的，也就是说T1-T3，这三个是不需要再次计算size的，我们只需要计算上图那两个白色的节点的size即可！

又因为，旋转之后，新的根节点的节点数，还应该是原根节点的节点数，所以最后我们只需要计算旋转之后，原根节点的节点数即可，也就等于该节点的左子树节点数加上右子树的节点数，再加自己本身这个节点。

//SBT右旋转
private SBTNode R_Rotate(SBTNode node) {
    SBTNode newRoot = node.left;
    node.left = newRoot.right;
    newRoot.right = node; 
    
    //计算size
    newRoot.size = node.size; //新根节点的节点数，等于原根节点的节点数
    node.size = (node.left != null? node.left.size : 0) + 
        (node.right != null? node.right.size : 0) + 1;
    return newRoot; //返回新的根节点
}

左旋转：(RR型)

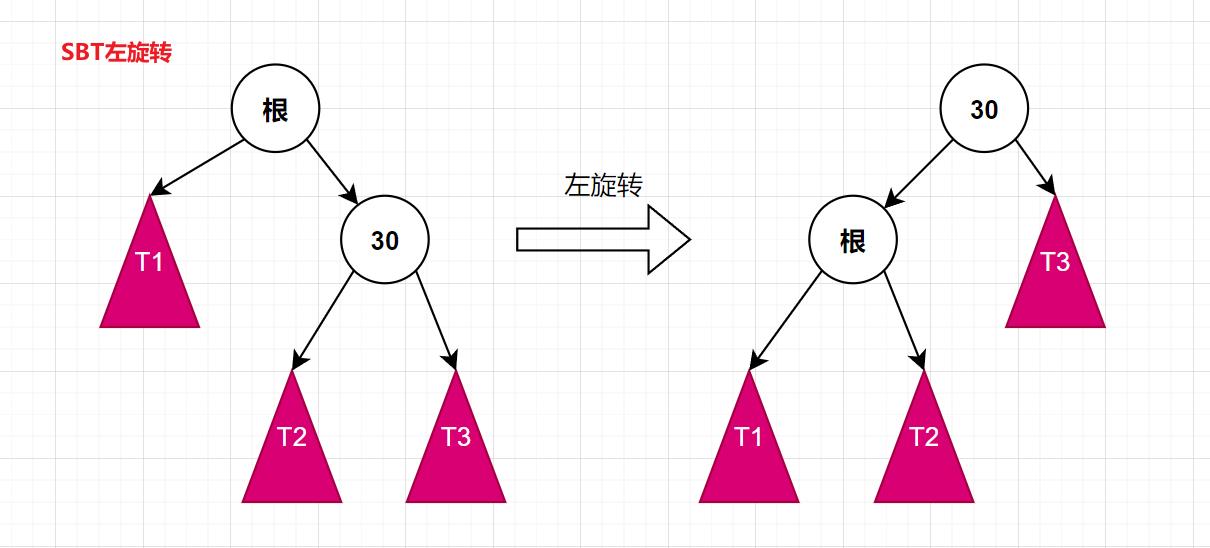
跟上面的旋转一样，每个节点之间的指针指向，这里就不深究了，同学可以看看我前期的文章，有讲解。主要还是size的计算，同样的，T1~T3的节点数，都是没有变，所以不用管。只需计算原根节点和新根节点的节点数，切新根节点的节点数，就是原根节点的节点数。

//SBT左旋转操作
private SBTNode L_Rotate(SBTNode node) {
    SBTNode newRoot = node.right;
    node.right = newRoot.left;
    newRoot.left = node;
    
    //计算size
    newRoot.size = node.size; //继承原根节点的节点数
    node.size = (node.left != null? node.left.size : 0) + 
        (node.right != null? node.right.size : 0) + 1;
    return newRoot; //返回新的根节点
}

以上两种就是最基本的LL型和RR型，在SBT中，也是有LR型和RL型的，跟AVL中一样，不需要再写额外的代码，只需要调用两次左旋转或者右旋转。如下：

• 假设A节点需要进行LR型的旋转，则只需A.left = 左旋转一次，再A= 右旋转一次。
• 同理，假设B节点需要进行RL型的旋转，则只需B.right = 右旋转一次，再B = 左旋转一次。

具体在什么时候需要调用旋转函数，我们在接下来的Maintain方法里讲解。

二、Maintain方法

Maintain方法，就是SBT树，最核心的地方，也就是这个方法，能够保证一棵树具有平衡性的。

首先，我们需要知道，在什么时候，才需要进行旋转操作。在AVL中，是通过判断平衡因子来处理平衡性；在左倾红黑树中，则是根据每个节点颜色来处理平衡性。而SBT是：

首先看这张图：

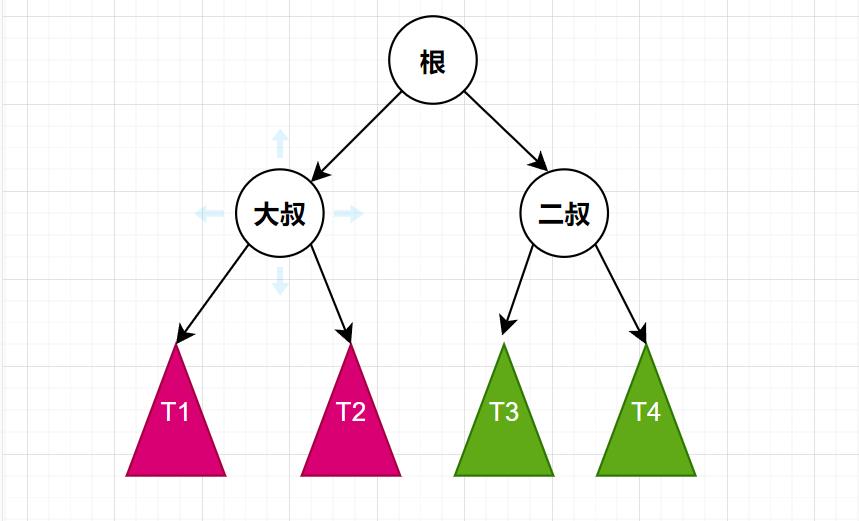
上面的四种旋转（LL、LR、RR、RL），分别对于一下四点：

• LL型：T1的size > 二叔的size
• LR型：T2的size > 二叔的size
• RL型：T3的size > 大叔的size
• RR型：T4的size > 大叔的size

以上四点，就是触发机关，只要满足这四点的某一个条件，则需要进行旋转操作。总结起来就一句话：叔叔的节点数，必须大于等于侄子的节点数。不然的话，就需要进行平衡调整。具体是为什么这种机制，就能够保证平衡性，请翻阅文章开头，陈启峰的那篇论文。

到目前为止，我们就知道了SBT的核心，代码写起来就简单多了，分别计算叔叔节点和侄子节点的节点数，if判断即可。值得注意的是，旋转操作之后，还需要递归调用Maintain方法。递归调用的对象，就是：哪个节点的子树被换了，则需要调用这个Maintain（新子树）；举个例子：原先A节点的右子树是T2，旋转操作之后，A节点的右子树变为了T3，那么就需要递归调用Maintain（T3）。

//Maintain方法
private SBTNode maintain(SBTNode cur) {
    if (cur == null) {
        return null;
    }

    //计算对应节点的节点数，null的话，就是0
    int leftSize = cur.left != null ? cur.left.size : 0;
    int rightSize = cur.right != null ? cur.right.size : 0;
    int leftLeftSize = cur.left != null ? (cur.left.left != null ? cur.left.left.size : 0) : 0;
    int leftRightSize = cur.left != null ? (cur.left.right != null ? cur.left.right.size : 0) : 0;
    int rightLeftSize = cur.right != null ? (cur.right.left != null ? cur.right.left.size : 0) : 0;
    int rightRightSize = cur.right != null ? (cur.right.right != null ? cur.right.right.size : 0) : 0;

    if (leftLeftSize > rightSize) { //LL型
        cur = R_Rotate(cur);//右旋
        
        cur.right = maintain(cur.right);
        cur = maintain(cur);
    } else if (leftRightSize > rightSize) { //LR型
        cur.left = L_Rotate(cur.left);
        cur = R_Rotate(cur);
        
        cur.left = maintain(cur.left);
        cur.right = maintain(cur.right);
        cur = maintain(cur);
    } else if (rightLeftSize > leftSize) { //RL型
        cur.right = R_Rotate(cur.right);
        cur = L_Rotate(cur);
        
        cur.left = maintain(cur.left);
        cur.right = maintain(cur.right);
        cur = maintain(cur);
    } else if (rightRightSize > leftSize) { //RR型
        cur = L_Rotate(cur);
        
        cur.left = maintain(cur.left);
        cur = maintain(cur);
    }
    return cur;
}

切记：递归调用Maintain时，一定是先调用cur的左右子树，然后才是调用cur。因为cur的处理，是依赖于他的左右孩子的。

可能有同学就会疑惑了，这么多递归函数，这个代码能跑完吗？

当然能够跑完，因为旋转操作之后，递归调用Maintain，能够在O(1)的时间内完成。

三、add方法和delete方法

Maintain方法之后，SBT的就算掌握大部分的代码了，其余的添加和删除代码，完全跟搜索二叉树的增加删除，一模一样。只是需要在添加删除之后，调用Maintain方法，用于调整平衡性即可。

//add方法
public void add(int val) {
    this.root = add(this.root, val);
}
//方法重载
private SBTNode add(SBTNode cur, int val) {
    if (cur == null) {
        return new SBTNode(val);
    } else {
        cur.size++; //沿途节点的节点数加1
        if (val < cur.val) {
            cur.left = add(cur.left, val);
        } else {
            cur.right = add(cur.right, val);
        }
    }
    //添加之后，需要调用maintain，进行平衡操作
    return maintain(cur); 
}

在SBT中，delete的时候，在大多时候，是不需要进行平衡调整的。why？

是因为没必要。假设当前SBT树的高度是H，现在删除一个节点后，高度可能还是H，又或者是H- 1。此时调整平衡与不调整平衡，都不影响后续的操作。比如删除之后，高度还是H，下次查找或者添加时，时间复杂度还是O(H)，影响因素还是高度值。所以在一些比赛中，为了达到优化，在delete中，不进行平衡性的调整。而是把平衡性的调整，放在了add方法里。

//delete方法
public void delete(int val) {
    if (contains(val)) { //包含当前值得话，就递归删除
        root = delete(root, val);
    }
}

private SBTNode delete(SBTNode cur, int val) {
    cur.size--; //沿途节点的节点数-1
    if (cur.val > val) {
        cur.left = delete(cur.left, val);
    } else if (cur.val < val) {
        cur.right = delete(cur.right, val);
    } else {
        if (cur.left == null && cur.right == null) { //没有左右子树
            cur = null;
        } else if (cur.left == null && cur.right != null) { //只有右子树
            cur = cur.right;
        } else if (cur.left != null && cur.right == null) { //只有左子树
            cur = cur.left;
        } else {
            //左右两个子树都有的情况
            SBTNode pre = null;
            SBTNode des = cur.right; //向右子树查找最左节点
            des.size--;
            while (des.left != null) {
                pre = des;
                des = des.left;
                des.size--; //最终的des节点，会重新计算节点数
            }
            if (pre != null) {
                pre.left = des.right;
                des.right = cur.right; //将des节点，替换cur节点
            }
            des.left = cur.left;//连接原先的左子树
            des.size = des.left.size + (des.right != null ? des.right.size : 0) + 1;
            cur = des;
        }
    }
    
    //cur = maintain(cur); //平衡调整
    return cur;
}

特别需要注意的是，就是被删除节点的左右子树都不为null时，需要找一个节点来替换当前被删除的节点。一般都是在被删除节点的右子树上，查找最小（最左）的节点进行替换。这一点，也是搜索二叉树的删除操作，最容易出错的一个点，值得重点关注。

还有一些简单的方法没写，大家自主实现即可。比如contains、isEmpty等等。

好啦。本期更新就到此结束啦！SBT树学好之后，可以帮助你在一些算法题上得到更好的帮助，这种结构也算比较好改。可能根据SBT改其他的结构。总之，这种结构，值得好好学习。

我们下期见吧！！！