基于Huffman树的文件压缩

Posted 2021-11-21 RONIN_WZ

基于Huffman树的文件压缩

• 一、开发环境
• 二、项目原理
• • 1. 文件在计算机是如何存储的？
  • 2. Huffman算法原理
• 三、项目流程
• • 1. 文件压缩
  • • 01 统计文件中字节出现的频次信息
    • 02 根据统计结果构建Huffman树
    • 03 通过Huffman树来获取每个字节对应的编码
    • 04 对待压缩文件进行改写
  • 2. 文件解压缩
  • • 01 从压缩文件头部获取解压缩所需的信息
    • 02 根据获取的信息重新构建Huffman树
    • 03 根据huffman树来获取每个字节对应的编码
    • 04 将压缩文件中的压缩编码进行转译

一、开发环境

vs2017

二、项目原理

1. 文件在计算机是如何存储的？

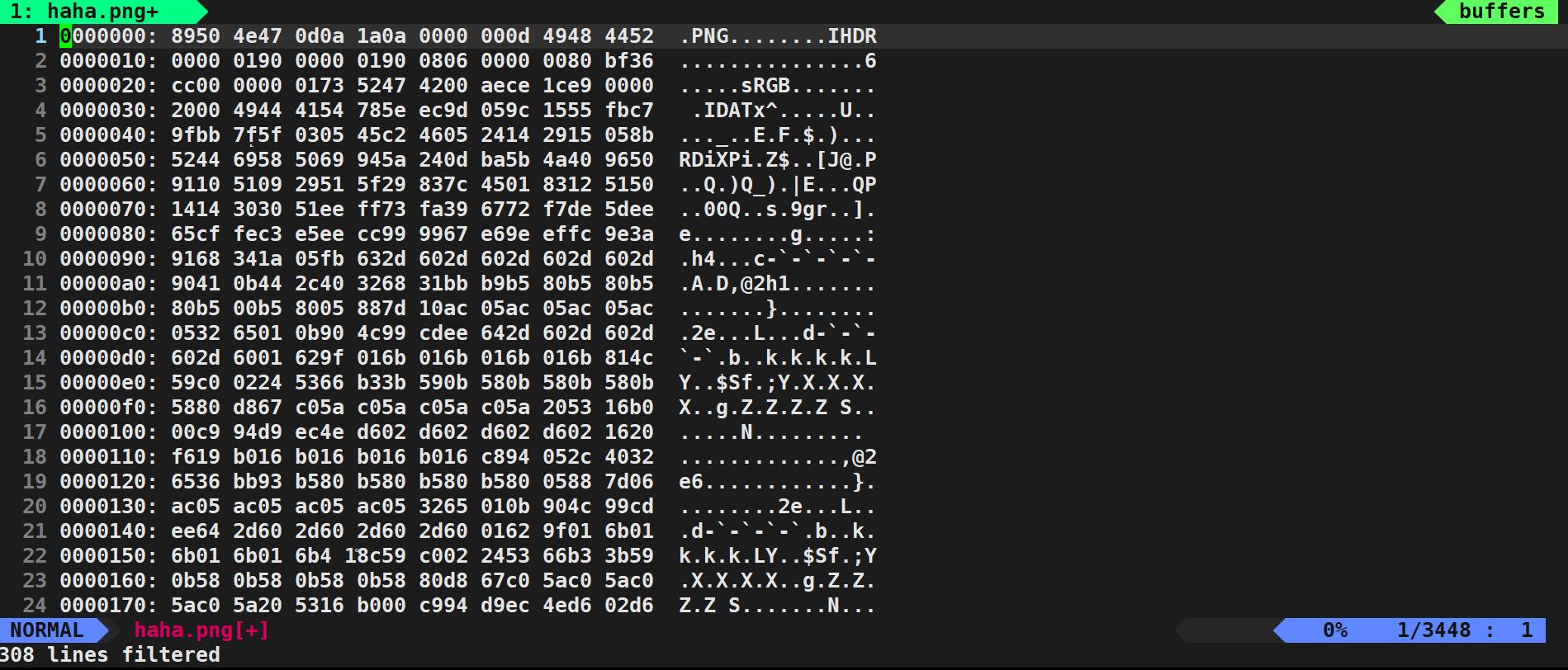
在我们所用的计算机中，计算机只认识0和1，所以所有文件的最终存储形式都是二进制形式（即0和1），像我们所看到的可视化图片视频，以及应用程序，都是通过某些特殊的协议进行解码得来的。
比如：

这张图片就是以下面的形式进行存储的

2. Huffman算法原理

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）
构造原理：
在一个文件中，每个字符有其各自的出现频率，若用一棵二叉树存储字符，我们希望出现频率较高的字母在二叉树上方，这样可以在遍历时效率更高。于是，我们在统计字符出现次数后，为字符分配相应的权值，权值较高的出现在二叉树上方。同时，二叉树的构造决定了它包含每个字母编码均不同。具体方法是，为每个左结点编码0，为每个右结点编码1，到达字母的0/1路径即组成了该字母的编码。
构造方法：

1. 每一次取出出现概率（权值）最小的两个节点作为新节点的子节点（小左大右），新节点的权值即左右子节点权值之和，然后将新的节点放入原数据集合中，递归。
2. 从建立好的哈夫曼树的头节点开始查找，找到叶子节点即返回一个数据，然后重新开始查找

三、项目流程

1. 文件压缩

01 统计文件中字节出现的频次信息

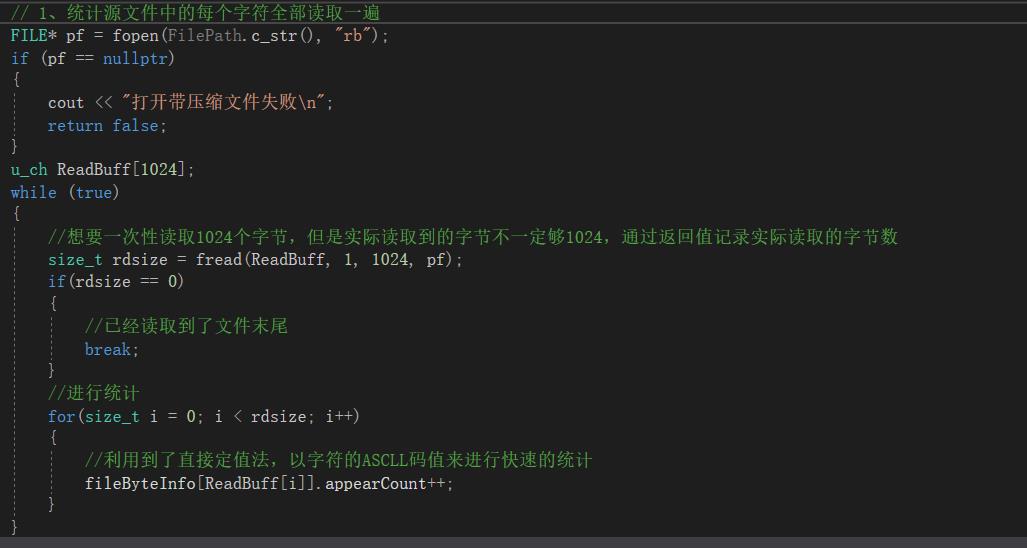
02 根据统计结果构建Huffman树

1. 根据所给的字节频次信息构建二叉树森林

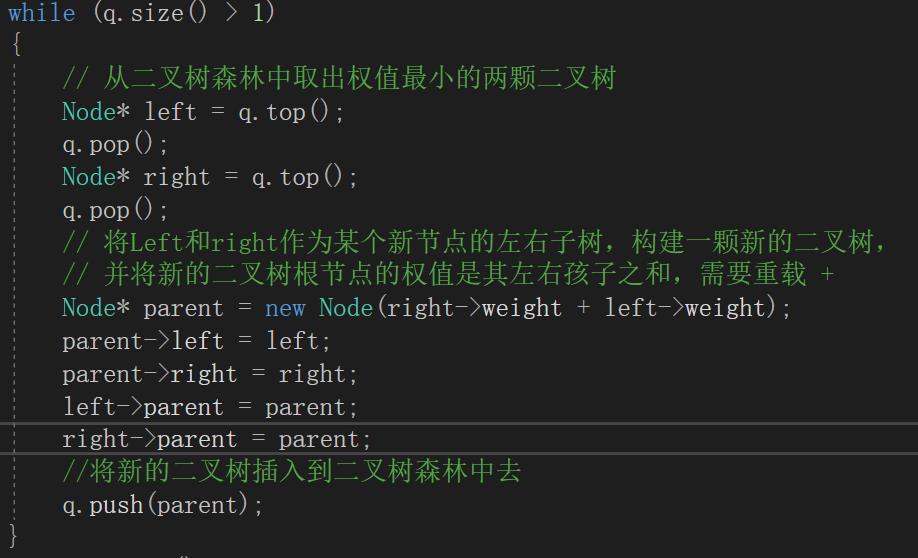
2. 循环进行以下操作直至二叉树森林中只有一颗二叉树为止：
   a. 从二叉树森林中选取根节点权值最小的两颗二叉树；
   b. 以这两棵二叉树作为某个结点的左右孩子创建二叉树，并更新根结点的权值；
   c. 将新二叉树放入二叉树森林中；
   

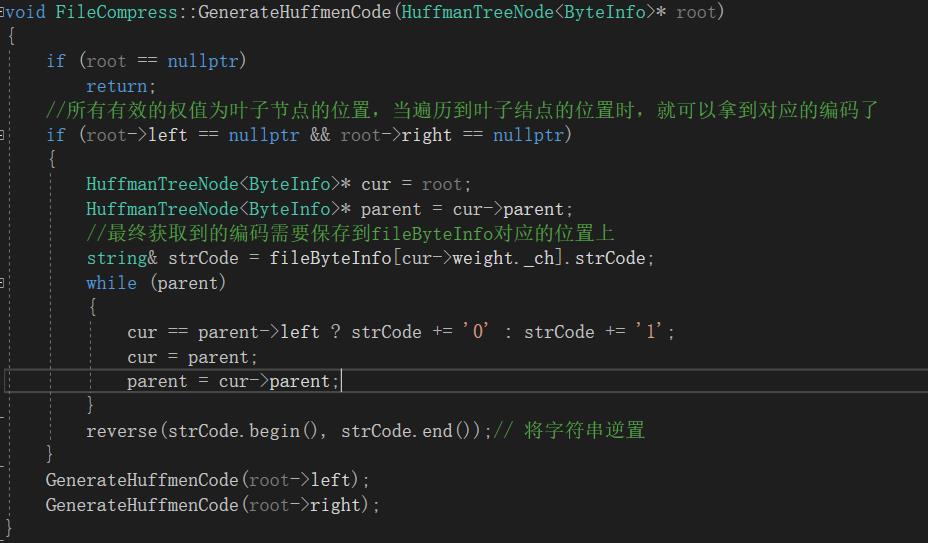
03 通过Huffman树来获取每个字节对应的编码

先遍历到叶子结点位置，在从叶子结点向根结点获取对应编码，所得到的编码与实际编码相反，所以需要将编码逆置

04 对待压缩文件进行改写

1. 先在压缩文件头部先写入源文件后缀以及字符的频次信息

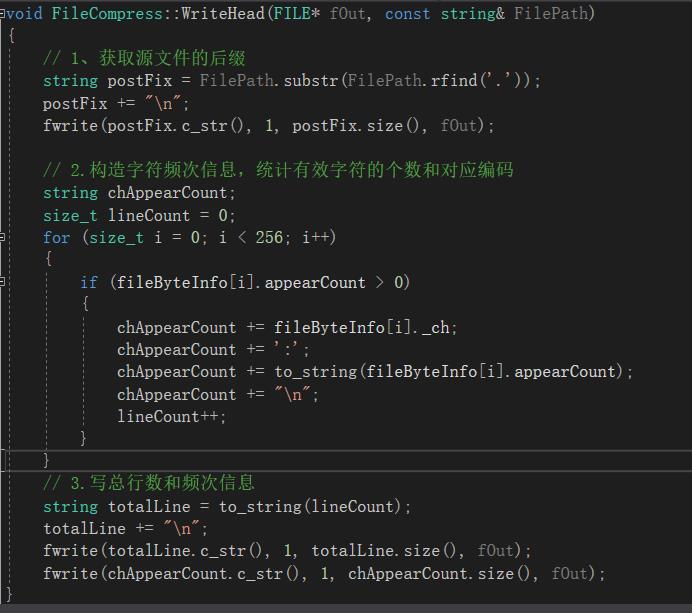
2. 用编码改写待压缩文件，将改写后的结果需要放置到压缩文件中保存

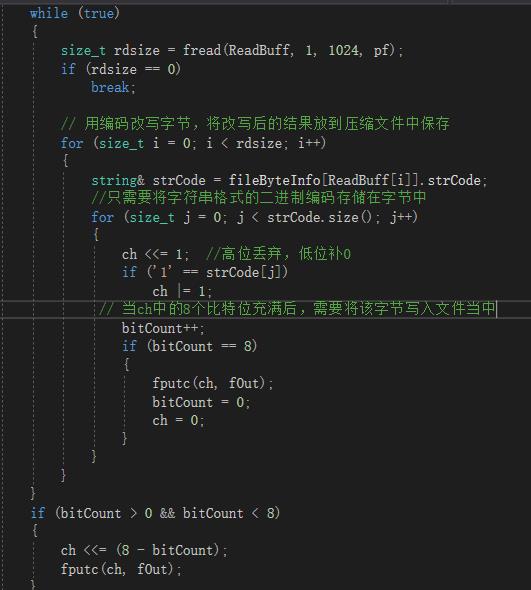
2. 文件解压缩

01 从压缩文件头部获取解压缩所需的信息

由于是按行读取，所以自己写了一个按行读取字符信息得函数

void FileCompress::GetLine(FILE* fIn, string& strContent)
{
	u_ch ch;
	while(!feof(fIn))
	{
		ch = fgetc(fIn);
		if (ch == '\\n')
			break;

		strContent += ch;
	}
}

从压缩文件头部获取解压缩文件所需的信息

	FILE* fIn = fopen(filePath.c_str(), "rb");
	if (fIn < 0)
	{
		cout << "打开压缩文件失败" << endl;
		return false;
	}
	// 读取源文件后缀
	string postFix;
	GetLine(fIn, postFix);
	// 读取频次信息总行数
	string strContent;
	GetLine(fIn, strContent);
	size_t lineCount = atoi(strContent.c_str());
	// 循环读取linecount行；获取字节的频次信息
	strContent = "";
	for (size_t i = 0; i < lineCount; ++i)
	{
		GetLine(fIn, strContent);
		if ("" == strContent)
		{
			//说明刚刚读取到的是一个换行
			strContent += '\\n';
			GetLine(fIn, strContent);
		}
		fileByteInfo[(unsigned char)strContent[0]].appearCount = atoi(strContent.c_str() + 2);
		strContent = "";
	}

02 根据获取的信息重新构建Huffman树

	ByteInfo invaild;
	HuffmanTree<ByteInfo> ht;
	ht.CreateHuffmanTree(fileByteInfo, 256,invaild);

03 根据huffman树来获取每个字节对应的编码

	GenerateHuffmenCode(ht.GetRoot());

04 将压缩文件中的压缩编码进行转译

	// 3.读取压缩数据，结合Huffman树进行解压缩
	string filename("3");
	filename += postFix;
	FILE* fOut = fopen(filename.c_str(), "wb");
	filename += postFix;
	unsigned char readBuff[1024];
	unsigned char bitCount = 0;
	HuffmanTreeNode<ByteInfo>* cur = ht.GetRoot();
	const int fileSize = cur->weight.appearCount;
	int compressSize = 0;
	while (true)
	{
		size_t rdsize = fread(readBuff, 1, 1024, fIn);
		if (0 == rdsize)
			break;
		for (size_t i = 0; i < rdsize; ++i)
		{
			//逐字节解压缩
			unsigned char ch = readBuff[i];
			bitCount = 0;
			while (bitCount < 8)
			{
				if (ch & 0x80)
					cur = cur->right;
				else
					cur = cur->left;
				bitCount++;
				if (nullptr == cur->left&&nullptr == cur->right)
				{
					fputc(cur->weight._ch, fOut);
					cur = ht.GetRoot();
					compressSize++;
					if (compressSize == fileSize)
						break;
				}
				ch <<= 1;
			}
		}
	}