P1020导弹拦截（超详细）(21.10.18)

Posted 2021-11-21 未定_

P1020 (NOIP1999 普及组 )导弹拦截
题意：某导弹拦截系统，其拦截的第一发炮弹可到达任意的高度，但以后每一发炮弹都不能高于前一发的高度。因此有可能不能拦截所有的导弹。输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

---

分析：
首先题目要读懂，以下有点啰嗦了，会的自动略过。
读题： 题目有两个问题，第一题最多能拦截多少个导弹？由于拦截系统的规则是每一发炮弹都不能高于前一发的高度，可以相等，易知找最长不升子序列，第二题最少要配备多少套这种导弹拦截系统？也就是问最长不升子序列有几个，再看题干，输入导弹依次飞来的高度，也就是导弹飞来的时间顺序固定，也就是序列的顺序固定，那只需要找最长上升子序列的长度即为配备导弹拦截系统的个数，为什么？序列从头开始比前面高的拦不了自然需要再加一个拦截系统了。
思考：
看了提示标签，可以用动态规划，贪心和二分做，时间复杂度不同。
先说O(n²):动态规划，只能过一半测试样例，另一半时间限制
比较基本的动态规划，不能全AC，不过多解释

#include<iostream>
#include<cstdio>
using namespace std;
int a[100005],b[100005],c[100005];//b[i]表示以第i个数为终点的最长不上升子序列的长度
int main()
{
    int x,n=1,sum1=0,sum2=0;
    while(~scanf("%d",&x))
    {
        a[n++]=x;
    }
    for(int i=1;i<n;i++)
    {
        b[i]=1;
        c[i]=1;
        for(int j=1;j<i;j++)
        {
            if(a[j]>=a[i])
                b[i]=max(b[i],b[j]+1);
        }
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
                c[i]=max(c[i],c[j]+1);
        }
        sum1=max(sum1,b[i]);
        sum2=max(sum2,c[i]);
    }
    printf("%d\\n%d",sum1,sum2);
}

再说O(nlogn):贪心+二分->参考自大佬博客
对于第一问，假设我们构建一个数组a[]存最长不升子序列，len表示a的最大下标。当我们从头扫描题干序列时，遇到一个数比a[len]小或者相等时，直接把它加到a[len]后面即可，即a[len++]，但如果比a[len]大时，理应跳过，现在我们考虑以下两种情况，设当前扫描到的数为y：
•如果a[len-1]>y>a[len]，根据贪心思想，肯定是序列a的末尾数越大越好，这样后面就可以接更多数。所以用y替换当前的a[len]，即a[len]=y。
•如果y>…>a[len-1]>a[len]，此时并不影响序列以后的连接。
以上两种情况怎么实现呢？分情况吗？懒人有更省事的做法。对于情况1，我们是不是可以理解为找数组a中第一个小于y的下标k，情况1是k=len，然后替换a[k]=y，这时你就会发现该做法代到情况2里也成立 ，因为序列a的末尾根本没受影响

举个例子：比如序列为｛9,7,3,5,4,2｝
前三个数直接放{9,7,3};
下一步扫描到5，如果跳过，最后的序列为{9,7,3,2}
但如果用5替换3，则｛9,7,5,4,2｝。
显然替换更合适，再比如序列为｛9,7,3,8,2｝
前3个数直接放{9,7,3};
下一步扫描到8，找到第一个小于8的数是7，若替换变成｛9,8,3,2｝与｛9,7,3,2｝的长度一样，并不影响找最长不升子序列的长度。

所以为啥不用更省事的方法呢🤔
（注意，替换的做法求得的序列不一定是符合题目要求的序列，但长度一定是符合题目要求的长度，原因就是第二种情况在长度不变的情况下把正确的序列换走了）
这时可能又有疑惑了，为啥要找第一个小于y的下标，小于等于表示不服。
我以亲身经历告诉你，还真不行。。。

举个最简单的例子：比如序列为｛9,7,5,3,5,4,2｝
前四个数直接放{9,7,5,3};
下一步扫描到5，如果与第一个小于5的元素3替换，则变成{9,7,5,5},继续，最后为{9,7,5,5,4,2}
但如果与第一个小于等于5的元素替换，则变为｛9,7,5,3｝,继续，最后为{9,7,5,3,2}
显然应该找第一个小于y的下标

怎么找第一个小于y的数哩，自己写个二分？懒人又有话说
•敲重点：

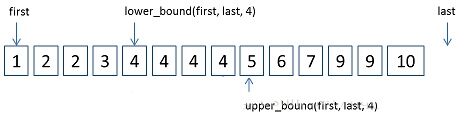
lower_bound会找出序列中第一个大于等于x的数
upper_bound会找出序列中第一个大于x的数
lower_bound与upper_bound都是在序列已经相对递增有序的基础上实现的
可是题目要求我们找的是降序列，怎么把相对递增变相对递减？以upper_bound()为例。

//第一种：自己写个cmp函数
bool cmp(const int& a,const int& b)
{    return a>b;
}
upper_bound(a+1,a+1+n,x,cmp);
//第二种：
#include<functional>
upper_bound(a + 1, a + 1 + n, x, greater <int> () );//内置类型的由大到小排序

这样第一问就可以轻松解决了，简单概括就是扫描数y小于等于a[len]就添到其末尾，否则就替换，最后数组a的长度就是最长不升子序列的长度。

第二问最长上升子序列,处理方式跟上面一样，把上面求减的改成求增的就可以啦。
具体分析一下：
假设我们构建一个数组b[]存最长上升子序列，len表示b的最大下标。当我们从头扫描题干序列时，遇到一个数比b[len]大时，直接把它加到b[len]后面即可，即b[len++]，但如果比b[len]小或者相等时，同上面一样的方法，不可以跳过，而是替换。我们可以这样理解，每次替换就相当于把该数与待替换的数联合成一个不升子序列，不好理解就看个例子：

这里该找序列中第一个大于等于x的数还是第一个大于x的数呢？答：第一个大于等于x的数
从上图我们可以看出原始序列有两个3，当扫描到第二个3时，如果在上升序列里找第一个大于x的数根本找不到，所以应该找第一个大于等于x的数，而且，第一问求不升序列，我们替换的时候也是在变相构造不升序列的过程，当然应该加等号啦。

#include<iostream>
#include<functional>
#include<algorithm>
#include<cstring>
using namespace std;
int a[100005],b[100005],c[100005];
int main( )
{
    int n=0,sum1=0,sum2=0,x;
    while(cin>>x)
    {
        a[n++]=x;
    }
    b[0]=a[0];
    c[0]=a[0];
    for(int i=1; i<n; i++)
    {
        if(b[sum1]>=a[i])
        {
            b[++sum1]=a[i];
        }
        else
        {
            int t=upper_bound(b,b+sum1,a[i],greater<int>())-b;
            b[t]=a[i];
        }
        if(a[i]>c[sum2])
        {
            c[++sum2]=a[i];
        }
        else
        {
            int k=lower_bound(c,c+sum2,a[i])-c;
            c[k]=a[i];
        }
    }
    cout<<sum1+1<<endl<<sum2+1<<endl;
}

---

这题做的好不容易，虽然并不算很难，不过有很多细节需要好好注意。
如果你喜欢这篇文章，欢迎点赞评论哦~