OpenCV实战 | 一文剖析图像阈值化方法——adaptiveThreshold thresholdTHRESH_OTSU

Posted 2021-11-21 行路南

图像阈值化，是指根据图像内像素点强度的分布规律设置一个阈值，并根据像素点强度高于阈值或者低于阈值而进行一些处理。例如，输入是一张灰度图和一个阈值$T$，当图中像素值大于阈值$T$，则输出图像对应像素设置为255（白色）；当图中像素值小于等于阈值$T$，则输出图像对应像素设置为0（黑色），这样通过阈值化就得到了一个二值化的图像。阈值化作为一种非常普遍使用的图像预处理方式，有利于我们在图像中定位到我们的目标对象。

从上述阈值化的定义中，我们会发现存在两个关键问题：

• 合适的阈值如何设置？
• 阈值设置后，基于像素点与阈值的关系而进行的处理方式都有哪些？

1. 手动设置阈值

最简单粗暴的方式莫过于手动设置阈值。当我们拿到一张彩色图像并转换到灰度图后，我们可以打印出灰度图每个图像位置的灰度值。我们可以不断地尝试阈值，从而使得我们的目标对象被提取地很好。

在OpenCV中提供了阈值化的函数

double cv::threshold	(	InputArray 	src,
                            OutputArray 	dst,
                            double 	thresh,
                            double 	maxval,
                            int 	type 
                         )	

参数	参数含义
src	输入图像（支持多通道）
dst	输出图像
thresh	手动设置的阈值
maxval	图像像素的最大值
type	阈值处理的方式，见下图

c++示例代码

// 原始图像
Mat src = imread("/home/user/1.jpg");
// 转为灰度图
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
// 阈值化，像素点强度>200的设置为255，小于等于200的设置为0
Mat bw;
threshold(gray, bw, 200, 255, THRESH_BINARY);

手动设置阈值在针对一张特定图像的处理时，虽然我们会尝试若干次，但通常我们还是可以基本找到一个理想的值。但它的主要弊端是它的泛化值不好，可能在这张图像上效果很不错，换到另一张图像效果就大打折扣，原因可能只是另一张图像拍摄的光线、角度稍有不同等等。

因此我们需要有一种自动确定阈值的方法，能根据图像中像素强度的规律，找到一个合理的阈值。

2. OTSU 大津阈值法

大津阈值法假定图像中包含前景像素和背景像素，于是它计算能够将两类像素分类的最佳阈值，从而使得它们的类内方差最小，并证明了类内方差最小等价于类间方差最大。

为了形象的说明大津阈值法的效果，我们先举一个例子，让大家有一个直观的理解，最后我们会给出严谨的证明。

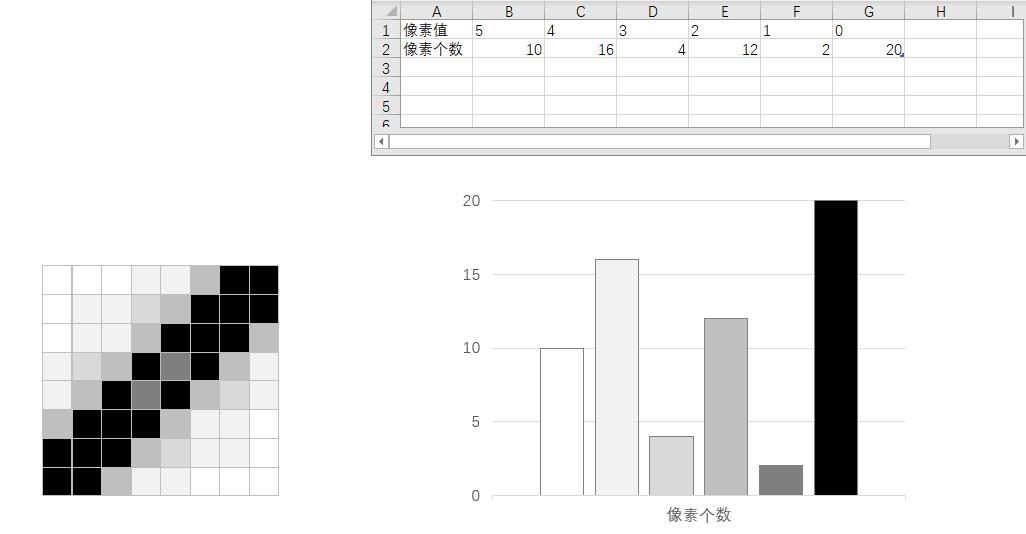
大津算法，是逐一计算每个阈值下的最小类内方差，找到最小的类内方差的阈值就是我们期望的阈值。

咱们以阈值$T=3$为例，来计算该阈值下的类内方差。

• 像素值小于等于3的为背景，背景像素的像素数量权重$w_b$、灰度均值${\mu }_b$和灰度方差${\sigma }_b^2$计算如下：

$$\begin{gathered} n_b=20+2+12+4=38 \\ n=8\ast 8=64 \\ {w}_b=\frac{n_b}{n}=\frac{38}{64} \\ {\mu }_b=\frac{0\ast 20+1\ast 2+2\ast 12+3\ast 4}{n_b}=\frac{38}{38}=1 \\ {\sigma }_b^2=\frac{(0-{\mu }_b{)}^2\ast 20+(1-{\mu }_b{)}^2\ast 2+(2-{\mu }_b{)}^2\ast 12+(3-{\mu }_b{)}^2\ast 4}{n_b}=\frac{48}{38}=1.26 \end{gathered}$$

• 像素值大于3的为前景，前景像素的像素数量权重$w_f$、灰度均值${\mu }_f$和灰度方差${\sigma }_f^2$计算如下：

$$\begin{gathered} n_f=16+10=26 \\ {w}_f=\frac{n_f}{n}=\frac{24}{64} \\ {\mu }_f=\frac{4\ast 16+5\ast 10}{n_f}=\frac{114}{24} \\ {\sigma }_f^2=\frac{(4-{\mu }_f{)}^2\ast 16+(5-{\mu }_f{)}^2\ast 10}{n_f}=\frac{9.625}{24}=0.4 \end{gathered}$$

• 根据背景的灰度方差${\sigma }_b^2$ 和${\sigma }_f^2$ 和对应的权重$w_b$ 和$w_f$, 求得类内方差为：
  σ T 2 = w b ∗ σ b 2 + w f ∗ σ f 2 = 0.898

  以上是关于OpenCV实战 | 一文剖析图像阈值化方法——adaptiveThreshold thresholdTHRESH_OTSU的主要内容，如果未能解决你的问题，请参考以下文章

  OpenCV实战 | 一文剖析图像阈值化方法——adaptiveThreshold thresholdTHRESH_OTSU

  OpenCV实战 | 一文剖析图像阈值化方法——adaptiveThreshold thresholdTHRESH_OTSU

  《OpenCV:灰度图像阈值化分割常见方法总结及VC代码》

  OpenCV实战（10）——积分图像详解

  OpenCV-Python实战——OpenCV用于图像分割的阈值技术（含大量示例，建议收藏）

  opencv学习之路（13）图像阈值化