车间调度基于matlab模拟退火算法求解车间调度问题含Matlab源码 894期
Posted 紫极神光
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了车间调度基于matlab模拟退火算法求解车间调度问题含Matlab源码 894期相关的知识，希望对你有一定的参考价值。
一、车间调度简介
1 车间调度定义
车间调度是指根据产品制造的合理需求分配加工车间顺序，从而达到合理利用产品制造资源、提高企业经济效益的目的。车间调度问题从数学上可以描述为有n个待加工的零件要在m台机器上加工。问题需要满足的条件包括每个零件的各道工序使用每台机器不多于1次，每个零件都按照一定的顺序进行加工。
2 传统作业车间调度
传统作业车间带调度实例
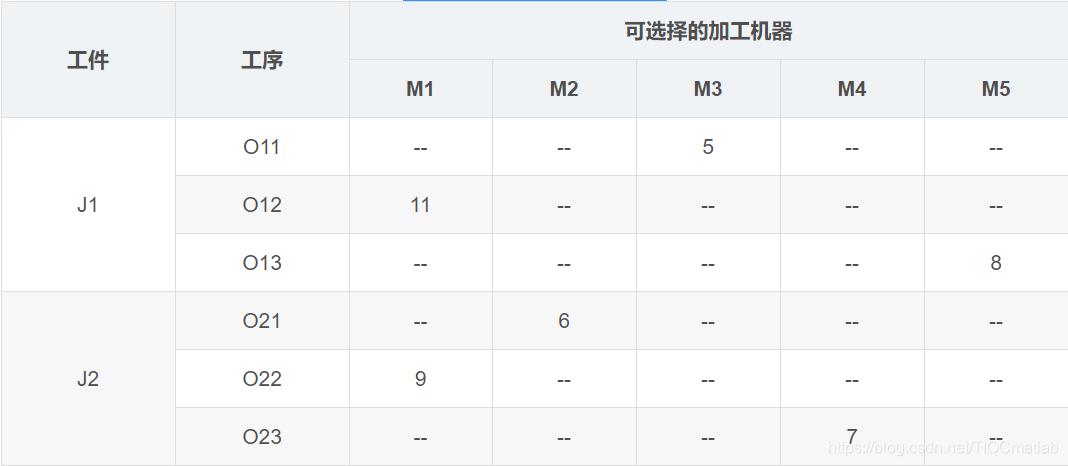
有若干工件，每个工件有若干工序，有多个加工机器，但是每道工序只能在一台机器上加工。对应到上面表格中的实例就是，两个工件，工件J1有三道工序，工序Q11只能在M3上加工，加工时间是5小时。
约束是对于一个工件来说，工序的相对顺序不能变。O11->O12->O13。每时刻，每个工件只能在一台机器上加工；每个机器上只能有一个工件。
调度的任务则是安排出工序的加工顺序，加工顺序确定了，因为每道工序只有一台机器可用，加工的机器也就确定了。
调度的目的是总的完工时间最短（也可以是其他目标）。举个例子，比如确定了O21->O22->O11->O23->O12->O13的加工顺序之后，我们就可以根据加工机器的约束，计算出总的加工时间。
M2加工O21消耗6小时，工件J2当前加工时间6小时。
M1加工O22消耗9小时，工件J2当前加工时间6+9=15小时。
M3加工O11消耗5小时，工件J1当前加工时间5小时。
M4加工O23消耗7小时，工件J2加工时间15+7=22小时。
M1加工O12消耗11小时，但是要等M1加工完O22之后才开始加工O12，所以工件J1的当前加工时间为max(5,9)+11=20小时。
M5加工O13消耗8小时，工件J2加工时间20+8=28小时。
总的完工时间就是max(22,28)=28小时。
2 柔性作业车间调度
柔性作业车间带调度实例（参考自高亮老师论文
《改进遗传算法求解柔性作业车间调度问题》——机械工程学报）
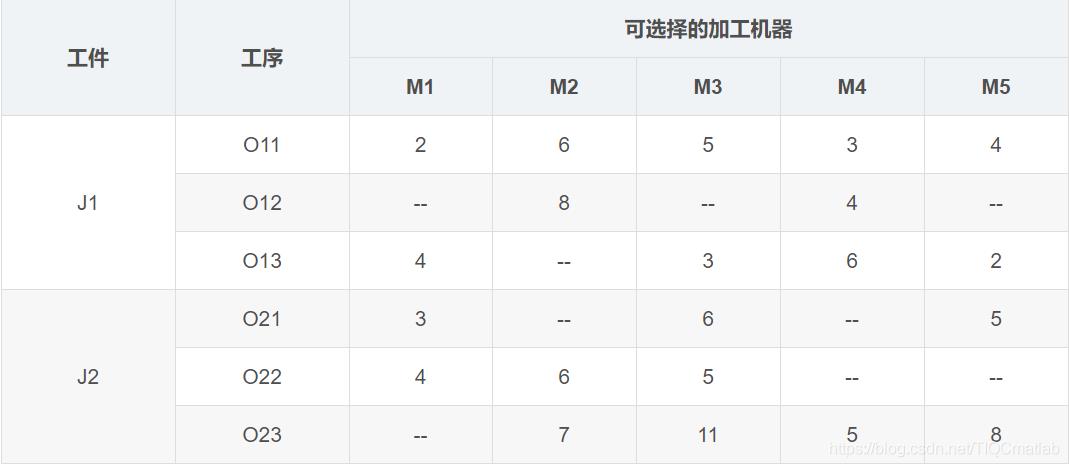
相比于传统作业车间调度，柔性作业车间调度放宽了对加工机器的约束，更符合现实生产情况，每个工序可选加工机器变成了多个，可以由多个加工机器中的一个加工。比如上表中的实例，J1的O12工序可以选择M2和M4加工，加工时间分别是8小时和4小时，但是并不一定选择M4加工，最后得出来的总的完工时间就更短，所以，需要调度算法求解优化。
相比于传统作业车间，柔性车间作业调度的调度任务不仅要确定工序的加工顺序，而且需要确定每道工序的机器分配。比如，确定了O21->O22->O11->O23->O12->O13的加工顺序，我们并不能相应工序的加工机器，所以还应该确定对应的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的机器组合。调度的目的还是总的完工时间最短（也可以是其他目标，比如机器最大负荷最短、总的机器负荷最短）
二、模拟退火算法简介
1 模拟退火算法的应用背景
模拟退火算法提出于1982年。Kirkpatrick等人首先意识到固体退火过程与优化问题之间存在着类似性；Metropolis等人对固体在恒定温度下达到热平衡过程的模拟也给他们以启迪。通过把Metropolis 算法引入到优化过程中，最终得到一种对 Metropolis 算法进行迭代的优化算法，这种算法类似固体退火过程，称之为“模拟退火算法”。
模拟退火算法是一种适合求解大规模组合优化问题的随机搜索算法。目前，模拟退火算法在求解 TSP，VLSI 电路设计等组合优化问题上取得了令人满意的结果。将模拟退火算法同其它的计算智能方法相结合，应用到各类复杂系统的建模和优化问题中也得到了越来越多的重视，已经逐渐成为一种重要的发展方向。
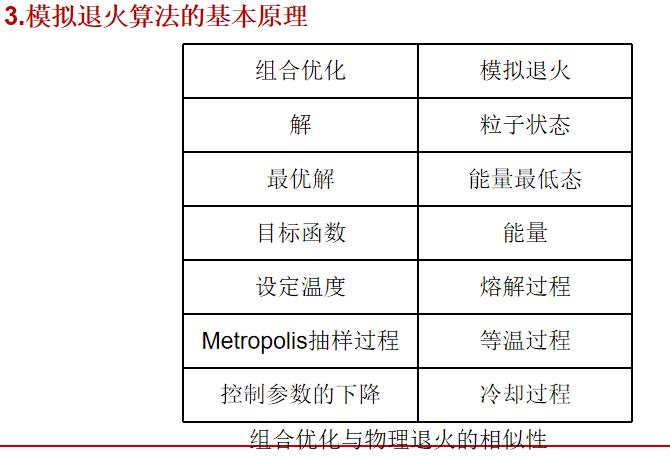
2 模拟退火算法介绍
3 模拟退火算法的参数
模拟退火是一种优化算法，它本身是不能独立存在的，需要有一个应用场合，其中温度就是模拟退火需要优化的参数，如果它应用到了聚类分析中，那么就是说聚类分析中有某个或者某几个参数需要优化，而这个参数，或者参数集就是温度所代表的。它可以是某项指标，某项关联度，某个距离等等。
二、部分源代码
clc;
clear;
close all;
%% Problem Definition
model=CreateModel(); % Create Model of the Problem
CostFunction=@(q) MyCost(q,model); % Cost Function
nVar=model.nVar; % Number of Decision Variables
VarSize=[1 nVar]; % Size of Decision Variables Matrix
%% SA Parameters
MaxIt=500; % Maximum Number of Iterations
MaxIt2=25; % Maximum Number of Inner Iterations
T0=10; % Initial Temperature
alpha=0.97; % Temperature Damping Rate
%% Initialization
% Create Initial Solution
x.Position=CreateRandomSolution(model);
[x.Cost, x.Sol]=CostFunction(x.Position);
% Update Best Solution Ever Found
BestSol=x;
% Array to Hold Best Cost Values
BestCost=zeros(MaxIt,1);
% Set Initial Temperature
T=T0;
%% SA Main Loop
for it=1:MaxIt
for it2=1:MaxIt2
% Create Neighbor
xnew.Position=CreateNeighbor(x.Position);
[xnew.Cost, xnew.Sol]=CostFunction(xnew.Position);
if xnew.Cost<=x.Cost
% xnew is better, so it is accepted
x=xnew;
else
% xnew is not better, so it is accepted conditionally
delta=xnew.Cost-x.Cost;
p=exp(-delta/T);
if rand<=p
x=xnew;
end
end
function model=CreateModel()
p=[ 48 27 18 15
23 52 50 59
35 39 25 10
45 38 36 49
55 56 18 51
58 24 40 54
37 48 23 14
17 48 43 30
17 29 45 23
23 38 48 50
52 13 32 32
22 12 14 56
51 37 21 19
22 49 56 23
57 57 17 17
27 16 52 16
20 39 37 54
22 33 60 39
41 10 13 38
34 27 32 17];
I=size(p,1);
J=size(p,2);
s(:,:,1)=[4 7 5 7 7 5 2 7 5 3 8 6 6 6 7 2 6 2 8 6
3 5 8 5 6 6 5 2 7 4 2 2 5 2 4 7 5 2 3 4
6 8 6 8 3 2 7 8 4 2 3 2 4 7 3 4 5 3 3 4
3 4 3 6 6 6 8 8 5 5 2 7 2 2 2 6 6 3 4 5
2 7 3 6 2 4 3 8 2 4 5 8 7 2 7 8 2 4 2 4
7 4 4 7 6 2 3 8 3 3 2 5 4 6 3 5 4 4 6 4
3 7 7 8 6 5 5 7 6 3 8 2 6 4 4 6 7 3 4 5
5 7 7 8 7 3 6 5 4 8 3 7 7 6 5 7 6 3 8 7
6 4 7 2 8 2 4 3 8 6 2 4 2 7 3 5 2 8 4 4
4 3 4 8 8 3 3 4 2 5 4 4 2 6 6 6 2 6 6 5
7 7 5 6 7 3 8 2 8 8 5 7 5 7 5 2 2 5 3 2
4 8 2 8 6 3 2 2 5 2 2 2 5 3 3 8 2 3 4 2
6 4 2 5 8 2 2 8 6 7 8 2 8 7 7 3 4 3 3 4
6 6 2 5 6 6 2 4 8 7 4 6 7 8 2 3 6 2 7 4
5 5 6 7 2 3 3 4 4 5 4 6 7 8 4 7 7 8 8 6
2 7 5 3 2 5 6 4 4 3 2 5 2 2 3 5 5 6 4 8
4 7 3 5 8 6 6 5 5 6 4 7 2 4 5 7 2 5 6 8
4 3 5 8 5 5 2 6 7 4 2 6 2 4 2 4 6 4 4 5
3 8 3 6 7 5 8 2 7 2 5 7 7 6 4 3 2 3 5 3
3 8 2 7 3 5 7 7 2 3 7 4 8 6 2 2 2 6 7 7];
s(:,:,2)=[7 7 7 6 3 3 2 4 7 2 5 7 3 5 4 4 5 8 4 5
7 7 3 4 4 3 3 6 6 3 5 4 3 5 2 2 6 5 6 3
7 2 2 8 2 5 3 7 2 2 8 5 6 8 3 3 4 7 8 8
2 5 7 3 6 3 2 6 7 5 7 8 6 4 3 7 2 6 7 7
6 4 6 6 3 7 2 5 8 3 5 5 6 5 4 7 5 2 5 8
5 5 7 6 2 8 6 6 7 8 8 4 6 8 3 8 4 5 7 3
3 4 6 4 7 2 8 5 2 2 2 6 2 2 4 6 7 6 4 6
2 4 4 2 4 5 4 2 4 2 4 4 4 8 2 2 7 5 8 6
7 3 4 2 6 2 4 7 6 5 8 7 5 3 8 8 6 4 8 2
3 3 7 4 4 7 8 8 7 7 8 4 3 6 2 7 2 8 8 4
3 2 4 3 6 8 8 4 3 4 6 5 7 6 8 4 2 7 4 3
6 8 7 7 2 2 6 8 3 3 6 6 7 6 4 5 5 7 5 7
8 6 7 4 8 8 8 4 6 4 4 8 3 4 2 8 4 4 3 3
5 8 7 7 7 2 7 8 5 3 8 4 7 6 4 7 8 6 7 8
6 3 5 7 7 6 4 5 6 5 2 7 2 7 7 7 8 8 8 7
3 8 6 5 7 7 6 4 3 8 7 7 7 2 7 5 4 8 8 4
8 7 8 3 4 5 3 3 3 6 6 8 2 2 5 5 7 6 5 5
5 6 5 8 6 8 4 2 7 2 7 2 6 8 6 5 8 3 6 6
6 5 2 3 6 8 6 4 7 4 4 4 4 6 8 3 6 6 3 7
2 3 8 8 5 6 5 7 8 2 7 6 7 3 2 7 8 2 8 6];
s(:,:,3)=[6 5 8 5 4 6 3 8 2 3 6 5 3 6 7 2 6 5 7 8
4 6 5 6 5 5 5 6 3 2 6 7 2 5 4 6 6 7 6 5
5 8 5 7 4 3 2 5 2 6 5 3 4 6 6 2 3 8 8 2
6 7 4 5 7 6 7 7 5 8 3 4 6 3 2 6 2 7 2 2
8 4 5 3 7 2 7 5 3 8 7 3 6 2 2 7 3 4 6 7
7 7 5 5 5 6 8 5 4 3 3 4 5 5 8 3 8 5 3 5
2 2 2 4 6 6 8 6 4 5 4 4 5 3 3 5 8 7 7 4
6 2 8 8 8 2 5 4 2 4 8 5 4 8 6 5 6 2 3 7
5 2 2 6 7 2 3 3 5 5 7 2 5 8 8 2 7 2 5 4
5 3 5 6 6 3 2 6 6 3 4 5 7 4 3 5 3 3 4 5
2 4 7 7 2 2 5 8 3 2 4 3 7 2 3 6 6 5 7 6
7 4 4 4 4 5 6 4 7 5 6 3 6 6 4 3 7 8 6 8
4 2 6 5 6 7 7 2 2 3 8 3 7 7 8 7 4 6 3 4
3 5 7 5 5 6 2 5 4 2 8 3 6 8 4 8 8 4 4 6
4 2 8 3 2 5 6 4 2 8 6 8 2 2 3 7 2 4 2 8
4 3 8 5 3 8 5 4 3 5 4 8 5 5 3 5 4 7 6 2
5 6 3 6 7 2 3 7 2 8 7 7 4 6 4 3 5 8 5 6
5 8 3 4 2 8 8 4 3 7 5 7 2 6 4 7 2 6 3 4
4 8 8 7 8 2 6 4 2 2 8 3 3 7 2 3 7 3 3 4
4 5 6 7 2 5 5 4 3 6 2 4 3 6 5 8 5 2 5 3];
s(:,:,4)=[7 7 8 3 8 2 5 2 3 8 2 5 7 7 3 4 7 6 8 7
8 5 2 3 6 7 6 4 7 6 4 8 5 8 8 4 7 3 5 6
3 3 2 4 4 4 8 8 4 6 7 7 4 3 6 以上是关于车间调度基于matlab模拟退火算法求解车间调度问题含Matlab源码 894期的主要内容，如果未能解决你的问题，请参考以下文章
车间调度基于matlab模拟退火算法求解车间调度(jobshop-3)问题含Matlab源码 1082期
车间调度基于matlab模拟退火算法求解车间调度(jobshop-3)问题含Matlab源码 1082期