SMOTE算法及其Python实现

Posted 2021-11-12 卖山楂啦prss

转载自：https://blog.csdn.net/Yaphat/article/details/52463304
作者：Yaphat

---

补充

---

转载正文：

SMOTE

SMOTE（Synthetic Minority Oversampling Technique），合成少数类过采样技术．它是基于随机过采样算法的一种改进方案，由于随机过采样采取简单复制样本的策略来增加少数类样本，这样容易产生模型过拟合的问题，即使得模型学习到的信息过于特别(Specific)而不够泛化(General)。

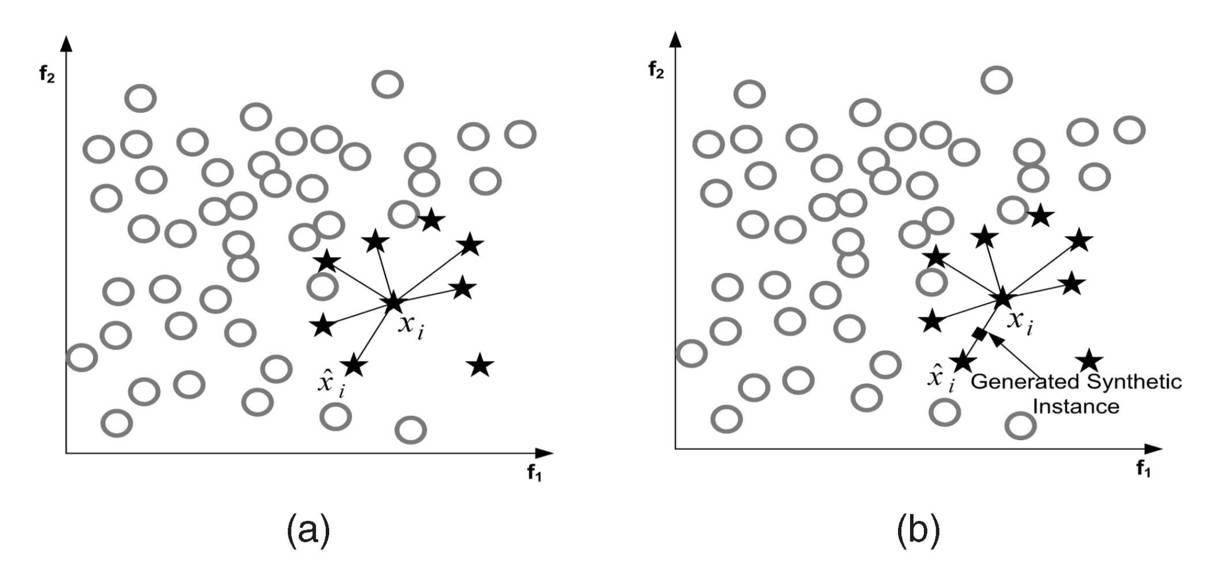
SMOTE算法的基本思想是对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中，具体如下图所示，算法流程如下。

$$x_{new}=x+rand\left(0,1\right)\times \left(\tilde{x}-x\right)$$

（1）对于少数类中每一个样本$x$，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其k近邻。

（2）根据样本不平衡比例设置一个采样比例以确定采样倍率$N$，对于每一个少数类样本$x$，从其 $k$ 近邻中随机选择若干个样本，假设选择的近邻为 $x_n$ 。

（3）对于每一个随机选出的近邻 $x_n$，分别与原样本按照如下的公式构建新的样本。

SMOTE算法的伪代码如下：

python代码实现如下：

import random
from sklearn.neighbors import NearestNeighbors    # k近邻算法

class Smote:
    def __init__(self,samples,N,k):
        self.n_samples,self.n_attrs=samples.shape
        self.N=N
        self.k=k
        self.samples=samples
        self.newindex=0

    def over_sampling(self):
        N=int(self.N)
        self.synthetic = np.zeros((self.n_samples * N, self.n_attrs))
        neighbors=NearestNeighbors(n_neighbors=self.k).fit(self.samples)    # 1.对每个少数类样本均求其在所有少数类样本中的k近邻
        for i in range(len(self.samples)):
            nnarray=neighbors.kneighbors(self.samples[i].reshape(1,-1),return_distance=False)[0]
            self._populate(N,i,nnarray)
        return self.synthetic
	# 2.为每个少数类样本选择k个最近邻中的N个；3.并生成N个合成样本
    def _populate(self,N,i,nnarray):
        for j in range(N):
            nn=random.randint(0,self.k-1)
            dif=self.samples[nnarray[nn]]-self.samples[i]
            gap=random.random()
            self.synthetic[self.newindex]=self.samples[i]+gap*dif
            self.newindex+=1

---

实际引用：https://work.datafountain.cn/forum?id=72&type=2&source=1

# 正负样本的比例大概在1:3左右
# 每个正样本用SMOTE方法随机生成两个新的样本
posDf = data[data['Churn'] == 1].drop(['Churn'], axis=1)    # 共1869条正样本, 取其所有特征列
posArray = posDf.values    # pd.DataFrame -> np.array, 以满足SMOTE方法的输入要求
newPosArray = Smote(posArray, 2, 5).over_sampling()
newPosDf = pd.DataFrame(newPosArray)    # np.array -> pd.DataFrame

# 调整为正样本在数据集中应有的格式
newPosDf.columns = posDf.columns    # 还原特征名
cateCols = list(newPosDf.columns.drop(['tenure', 'MonthlyCharges']))   # 提取离散特征名组成的列表
for i in cateCols:
    newPosDf[i] = newPosDf[i].apply(lambda x: 1 if x >= 0.5 else 0)    # 将特征值变回0、1二元数值
newPosDf['Churn'] = 1    # 添加目标变量列

print("原本的正样本有%d条" % posDf.shape[0])
print("原本的负样本有%d条" % (data.shape[0] - posDf.shape[0]))

原本的正样本有1869条
原本的负样本有5174条

为保证正负样本平衡，从新生成的样本中取出（5174 - 1869 = 3305）条样本，并加入原数据集进行shuffle操作。

# 构建类别平衡的数据集
from sklearn.utils import shuffle    

newPosDf = newPosDf[:3305]    # 直接选取前3305条样本
data = pd.concat([data, newPosDf])    # 竖向拼接
# data = shuffle(data).reset_index(drop=True)

print("此时数据集的规模为：", data.shape)

---

SMOTE算法的缺陷

该算法主要存在两方面的问题:一是在近邻选择时,存在一定的盲目性。

从上面的算法流程可以看出，在算法执行过程中，需要确定K值,即选择多少个近邻样本，这需要用户自行解决。

从K值的定义可以看出，K值的下限是M值(M值为从K个近邻中随机挑选出的近邻样本的个数,且有M< K)，M的大小可以根据负类样本数量、正类样本数量和数据集最后需要达到的平衡率决定。但K值的上限没有办法确定，只能根据具体的数据集去反复测试。因此如何确定K值，才能使算法达到最优这是未知的。

另外，该算法无法克服非平衡数据集的数据分布问题，容易产生分布边缘化问题。由于负类样本的分布决定了其可选择的近邻，如果一个负类样本处在负类样本集的分布边缘，则由此负类样本和相邻样本产生的“人造”样本也会处在这个边缘,且会越来越边缘化，从而模糊了正类样本和负类样本的边界，而且使边界变得越来越模糊。这种边界模糊性,虽然使数据集的平衡性得到了改善，但加大了分类算法进行分类的难度。

针对SMOTE算法的进一步改进

针对SMOTE算法存在的边缘化和盲目性等问题,很多人纷纷提出了新的改进办法，在一定程度上改进了算法的性能,但还存在许多需要解决的问题。

Han等人Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning 在SMOTE算法基础上进行了改进，提出了Borderhne.SMOTE算法，解决了生成样本重叠(Overlapping)的问题该算法在运行的过程中，查找一个适当的区域，该区域可以较好地反应数据集的性质,然后在该区域内进行插值，以使新增加的“人造”样本更有效。这个适当的区域一般由经验给定,因此算法在执行的过程中有一定的局限性。

SMOTE算法的论文地址：https://www.jair.org/media/953/live-953-2037-jair.pdf

我找到的SMOTE相关论文请转到我的另外一篇博客。