NTU 课程辅助笔记: NFA到DFA的转化
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了NTU 课程辅助笔记: NFA到DFA的转化相关的知识,希望对你有一定的参考价值。
我们以这张图为例:
用 Finite State Machine Designer - by Evan Wallace (madebyevan.com) 画的,有几条边的mark没画好错位了
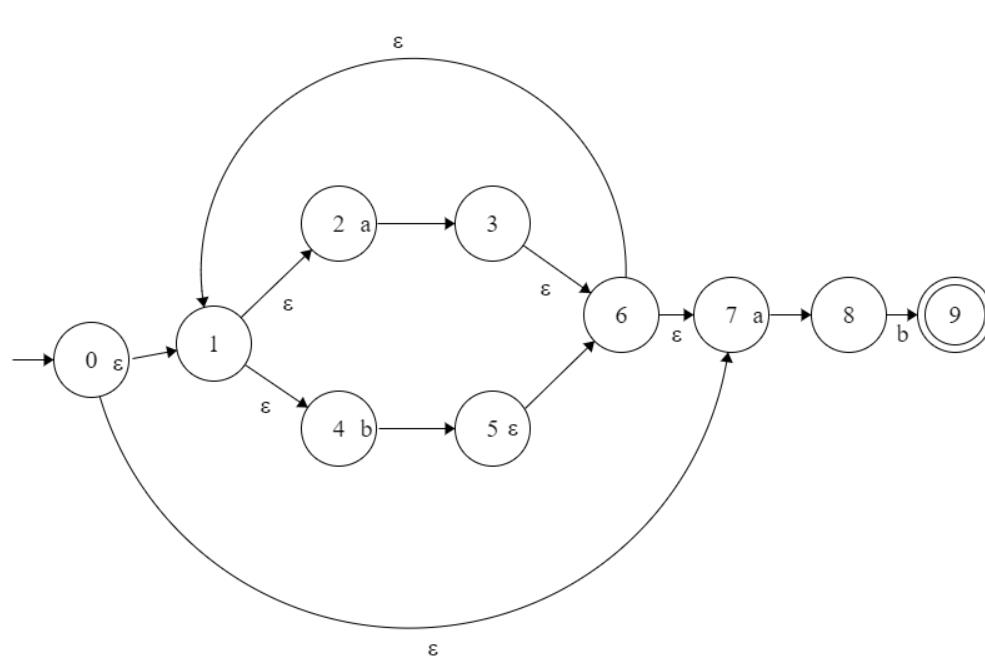
1 写出状态转换表
行index表示状态,列index表示条件,表格内的是后继状态
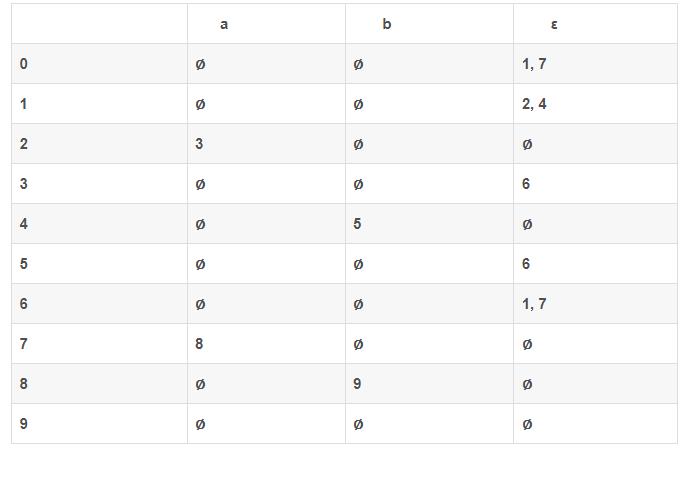
2 求出ε-闭包 (ε-closure)
ε-closure(s)表示由状态s经由条件ε可以到达的 所有状态的集合(包括自身)
| ε-closure(0) | {0,1,2,4,7} |
| ε-closure(1) | {1,2,4} |
| ε-closure(2) | {2} |
| ε-closure(3) | {1,2,3,4,6,7} |
| ε-closure(4) | {4} |
| ε-closure(5) | {1,2,4,5,6,7} |
| ε-closure(6) | {1,2,4,6,7} |
| ε-closure(7) | {7} |
| ε-closure(8) | {8} |
| ε-closure(9) | {9} |
3 将初始态的转换闭包ε-closure(0)设为状态A
即A={0,1,2,4,7}
4 写出状态A经过上面转换图中所有转换条件得到的状态的ε 闭包
- ε-closure(0) = A={0,1,2,4,7}
- ε-closure(move(A,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B
- ε-closure(move(A,b)) = ε-closure(5) = {1,2,4,5,6,7} = C
- ε-closure(move(B,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B
- ε-closure(move(B,b)) = ε-closure({5,9}) = {1,2,4,5,6,7,9} = D
- ε-closure(move(C,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B
- ε-closure(move(C,b))= ε-closure(5) = {1,2,4,5,6,7} = C
- ε-closure(move(D,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B
- ε-closure(move(D,b)) = ε-closure(5) = {1,2,4,5,6,7} = C
5 画出DFA 状态转换表
| a | b | |
| A | B | C |
| B | B | D |
| C | B | C |
| D | B | C |
6 画出DFA状态转换图
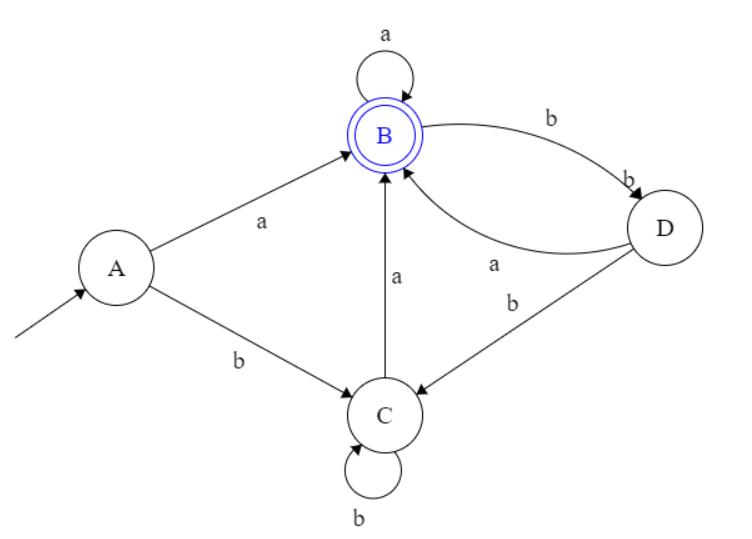
注:
7 DFA 最小化
7.1 消除多余状态
多余状态的特征:
1)从这个状态出发没有通路到达终态
2)从开始状态出发,任何输入串也不能到达的那个状态
举例说明:
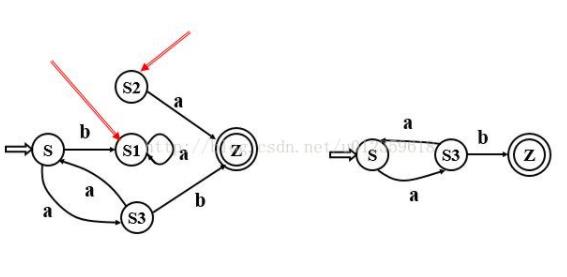
7.2 合并等价状态
等价状态的特征:
1) 一致性条件:状态s和t必须同时为终态或非终态
2)蔓延性条件:对于所有输入符号,状态s和状态t必须转化到等价的状态里
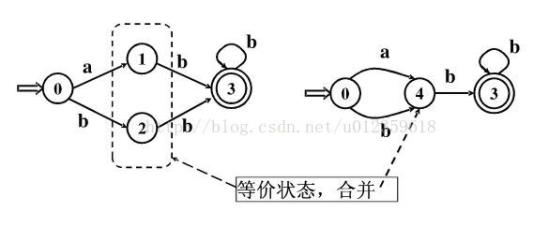
7.2.1 合并等价状态举例
(来自NFA到DFA的转化_只有十分努力,才能看起来毫不费力-CSDN博客_nfa转dfa)
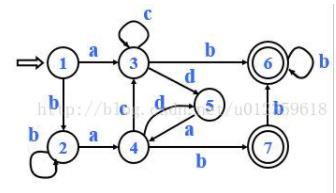
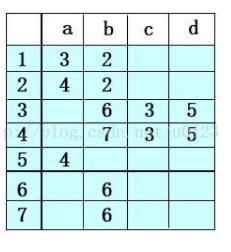
首先画出状态转移表
然后 我们看:
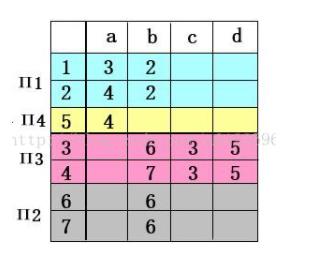
1)6和7同时是终态,满足条件1;同时6和7都能在b的情况下转换成6,所以这两个状态可以合并
2)然后我们就可以合并3和4
3)然后就可以合并1和2
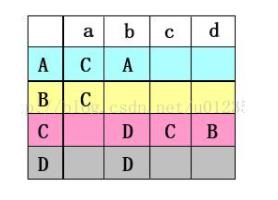
于是就有:
即:
8 我们的问题的优化DFA

| a | b | |
| A | B | C |
| B | B | D |
| C | B | C |
| D | B | C |
首先C和D可以合并:
| a | b | |
| A | B | E |
| B | B | E |
| E | B | E |
然后A和E可以合并
| a | b | |
| B | B | F |
| F | B | F |
B和F不能合并了,因为一个是终态,一个是非终态
所以简化后的DFA为
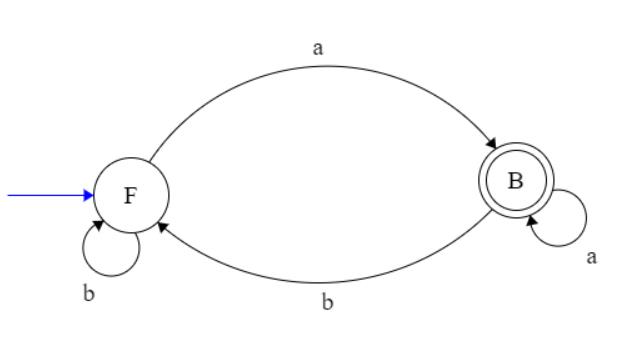
以上是关于NTU 课程辅助笔记: NFA到DFA的转化的主要内容,如果未能解决你的问题,请参考以下文章