CS224W摘要19.GNNs for Science

Posted 2021-11-11 oldmao_2000

文章目录

• Pre-Training GNN[^1]
• • Recap
  • 挑战
  • Pre-Training
  • 问题1
  • • Naïve 预训练设置与效果
    • Naïve 预训练效果分析
  • 预训练的正确做法
  • • Node Level Pre-Training（两个无监督任务）
    • Graph Level Pre-Training（一个有监督任务）
    • 小结及结果
• Hyperbolic Graph Embeddings[^2]
• • 表征空间的选择
  • 双曲空间模型
  • • hyperbolic geometry的相关定义
  • 双曲版GNN
  • 结果
• Design Space of GNN[^3]
• • 相关术语
  • • Design Space
    • Task Space
  • 模型的评估
  • • controlled random search
  • 实验结果1：GNN设计指南
  • 实验结果2：理解GNN相关任务
  • 实验结果3：设计迁移

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
这节课貌似三个部分，分别由尤里组中三个助教分别讲解。

Pre-Training GNN¹

GNN能有预训练？当然可以，但是不是乱上预训练模型性能就会变强，这个小节讨论了针对化学分子毒性预测任务做预训练的策略，这里要学会为什么预训练会变强的原理。

Recap

图机器学习常见的任务：
Chemistry: 分子图
任务：分子属性预测

Biology: Protein-protein 关联图
任务：蛋白质功能预测

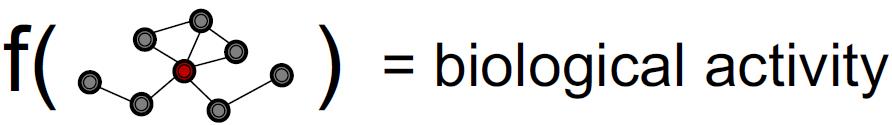
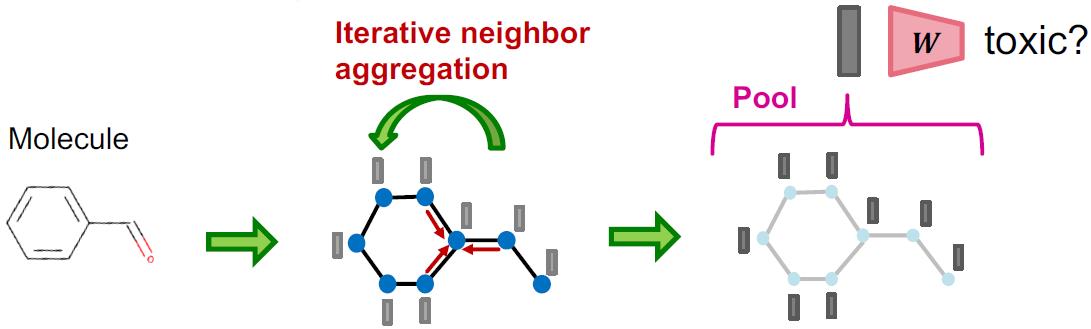
这里以分子毒性预测为例来讲，毒性预测可以看做图分类任务，图分类就要获取图的embedding，这个有两个步骤：

1. Iteratively aggregate neighboring information to obtain node embeddings
   这个步骤获取节点embedding实际上捕获的是局部邻域信息。
2. Pool node embeddings to obtain a graph embedding
   这个步骤是聚合所有（全局）节点的embedding信息。

挑战

1.标签数据很少。由于标签数据获取较为困难，因此GNN对于小的训练集容易过拟合。
尤其对于DL的模型，动不动就要训练上万个参数，从而导致：
#(Labeled training data) << #(Parameters)
更加导致DL模型容易在小的标记数据集上出现过拟合。
2.分布范围之外的预测。就是测试数据与训练数据长得不一样（属于不同分布），导致GNN的推断能力很差。
这里给了一个例子：

训练数据长这个样子，训练模型会把判别熊的种类的依据放到背景颜色上而非熊本身的特征，如果出现北极熊在青草上的图片，模型估计要扑街

根据两个挑战，我们的目标是：在少量数据样本的条件下提升模型对于分布之外数据的预测性能。
解决思想是：在对几乎没有标签的任务进行训练之前，将领域知识注入到模型中。（Inject domain knowledge）模型在训练前就有了领域知识后，模型就可以：
Generalize well without much task-specific labeled data在少量数据情况下，提升泛化性能。
Extract essential (non-spurious) pattern that allows better extrapolation.精炼重要的（非虚假的）模式，以便更好地进行推断。
Inject domain knowledge最有效的方法是：

Pre-Training

将模型通过拥有充足数据的相关任务进行预训练，就可以使得模型参数包含相关邻域知识。

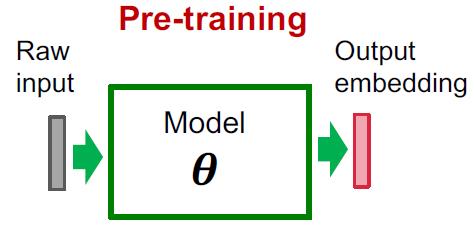
对于只有少量数据的下游任务，可以直接对参数进行fine-tuning，从而得到较好的效果。

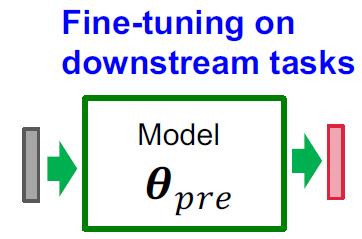
在CV和NLP领域，预训练都取得很好的效果，下面来考虑GNN的预训练模型。两个核心问题
How effective is pre-training GNNs?
What is the effective pre-training strategy?

问题1

pre-training GNN效果如何，先看下Naïve strategy咋整，本来是做分子毒性预测，现在label少，那就分子上带标签的相关任务训练一波

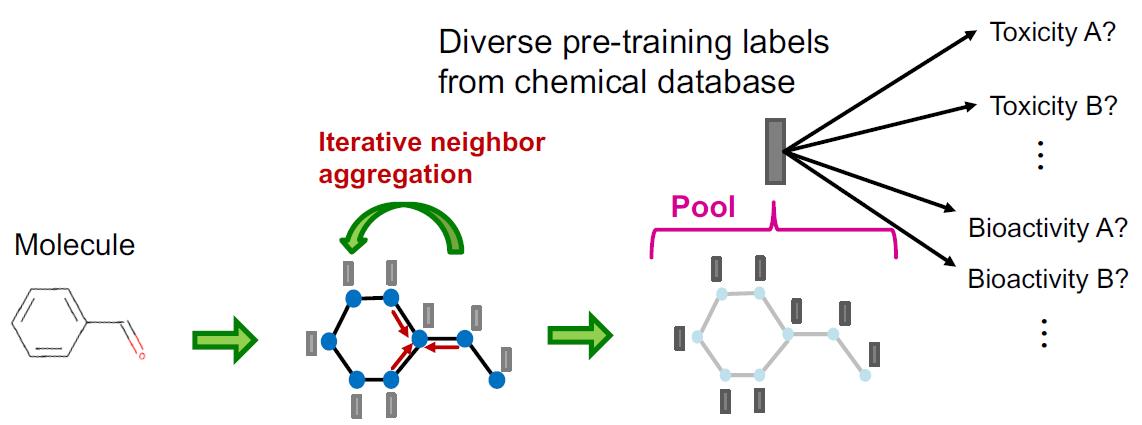
Naïve 预训练设置与效果

任务：二分类。使用ROC-AUC作为衡量标准

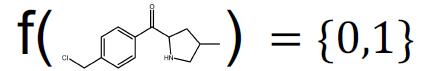
吃分子式，吐分类。

数据：有监督学习，所有数据带标签。
1310种不同的二元生物测定法，标注了约45万个分子
下游任务：这个是我们的真正目标，共有8个分子分类数据集，相对较小，每个约有1千到10万个分子。
数据划分：Scaffold，测试分子与训练数据不同分布。

Naïve 预训练效果分析

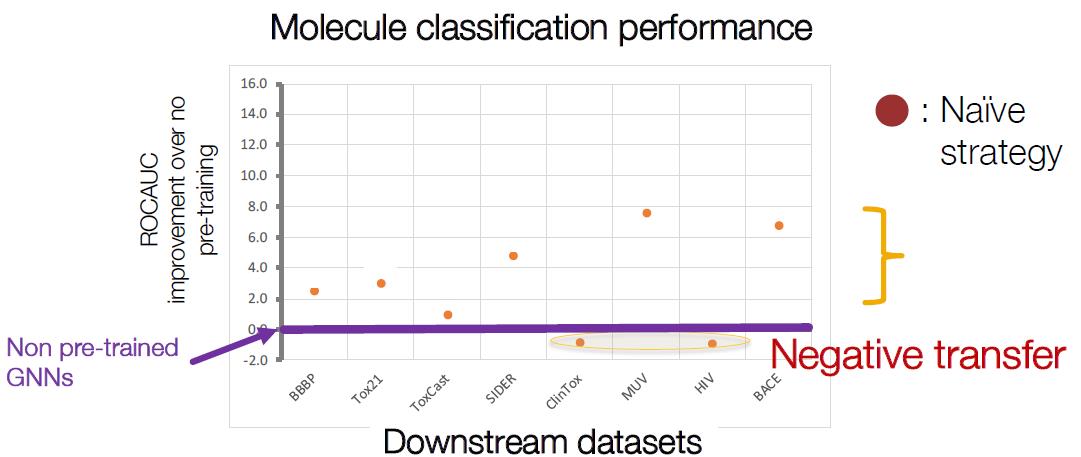
可以看到预训练GNN有效果，但是有两个数据集效果比原来没用预训练要差。上图紫色线是baseline。
分析原因，就是前面讲过，这个任务是图级别的分类任务，它涉及两个步骤，Naïve 只在单个步骤做了预训练：

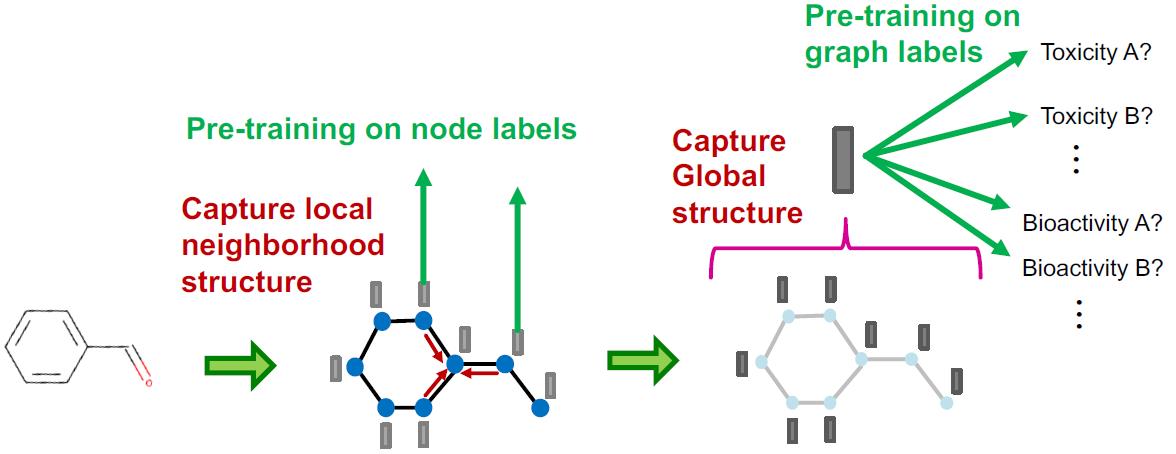
结果就是：

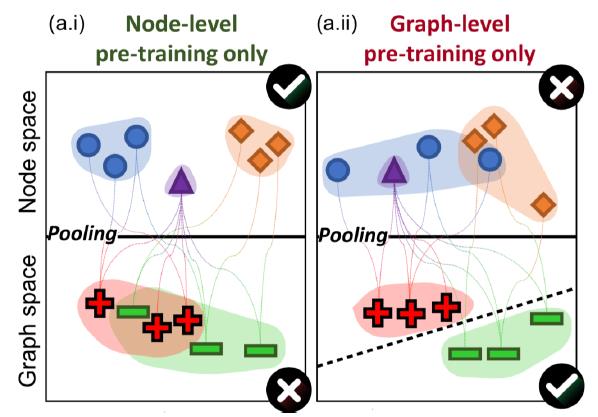
效果扑街的原因就是只做一个步骤的预训练，因此两个步骤都要做：

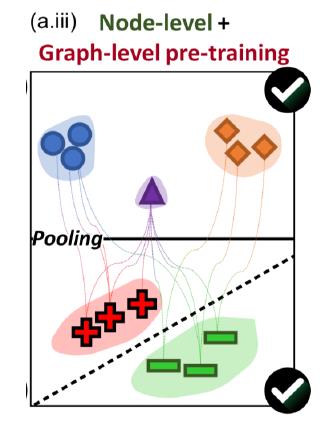
预训练的正确做法

就是两个步骤都做预训练，共涉及三个任务，两个无监督，一个有监督

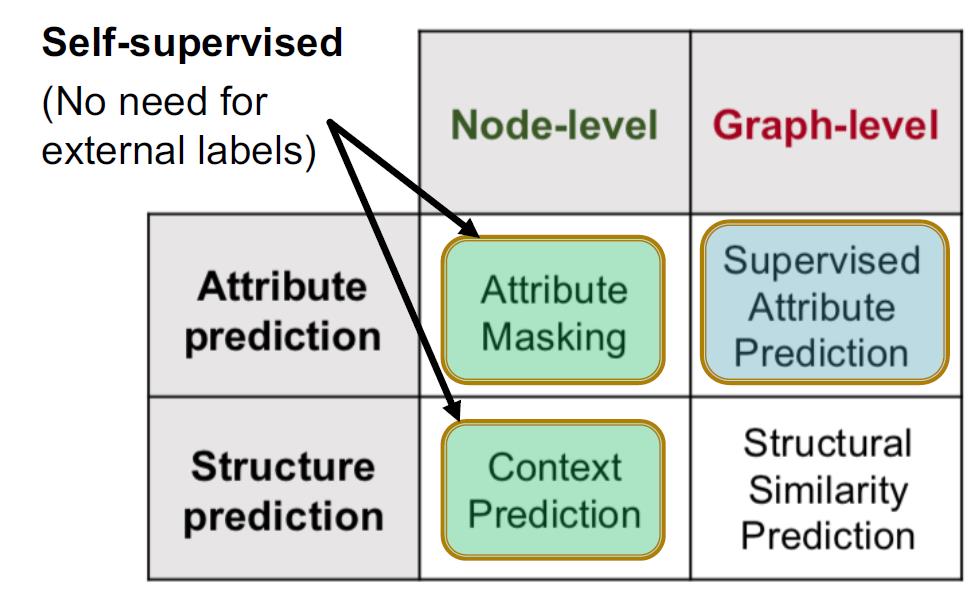
下面分别讲。

Node Level Pre-Training（两个无监督任务）

这个阶段一方面是知道周围节点预测中间节点，一方面是根据中间节点预测周围节点，听起来是不是和word2vec思想很像。
直接借鉴BERT的训练方法，Mask掉节点，然后让模型预测被Mask掉的节点。（这个方法不需要label1）

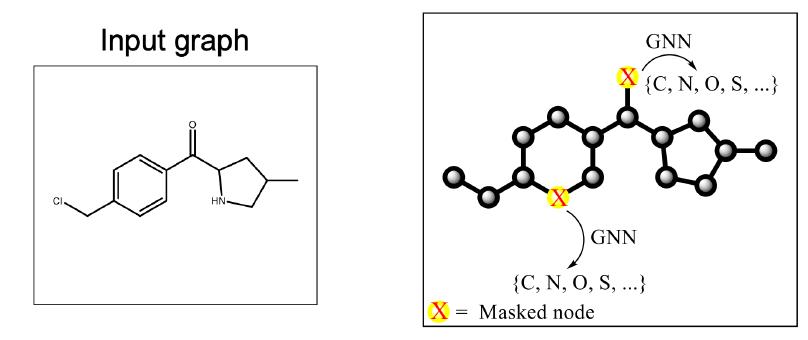
通过Mask节点，可以迫使模型学习到domain knowledge，这里的例子中可以学习到化学分子式的规则。
另外，还让模型做上下文的预测，具体做法是：

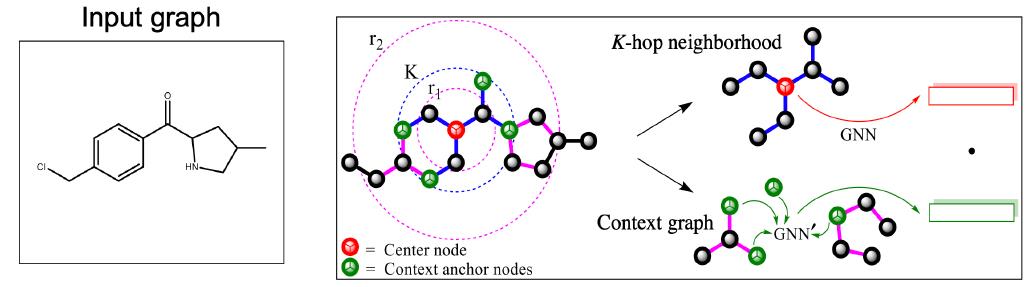
对每一个分子图，采样一个节点作为中心节点（上面红色点）；
然后分别提取中心节点的K跳邻居和上下文图context graphs，K跳邻居这个我们很熟悉，context graphs就是与中心节点一跳邻居相邻的图（上图中绿色节点往外2跳形成的图）
然后用GNN分别生成者两类图的embedding；
然后优化模型使得来自相同中心节点的K跳邻居和上下文图的embedding的内积越大越好，反之越小越好。
同样，这个任务也是无监督学习。其原理是相同结构或者相似结构的图往往语义上相同。

Graph Level Pre-Training（一个有监督任务）

这个就很直接，把相关任务的有标签分子式拿来，直接固定前面的参数，训练后面部分：

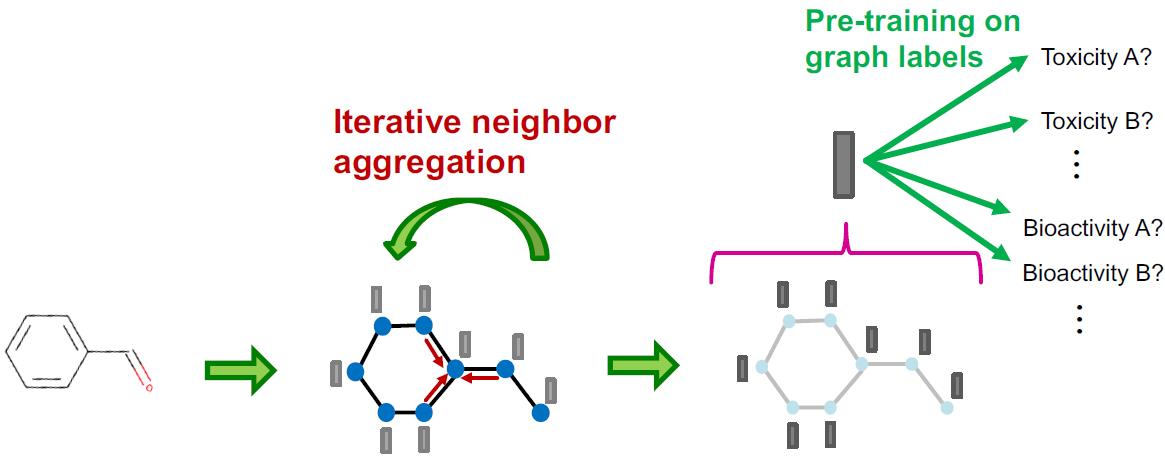
小结及结果

整个过程三个步骤：

1. Node-level pre-training
2. Graph-level pre-training
3. Fine-tuning on downstream tasks

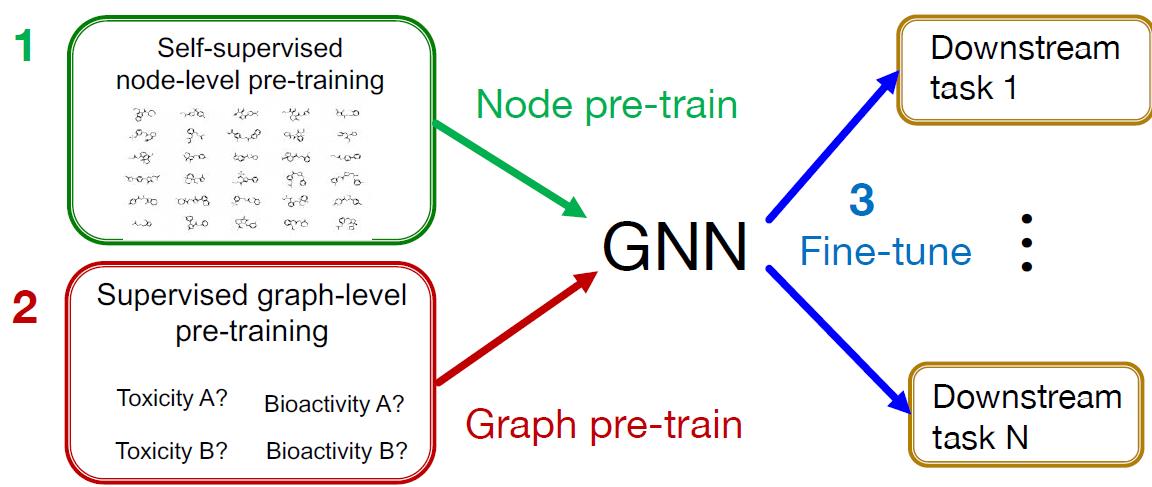
效果明显：

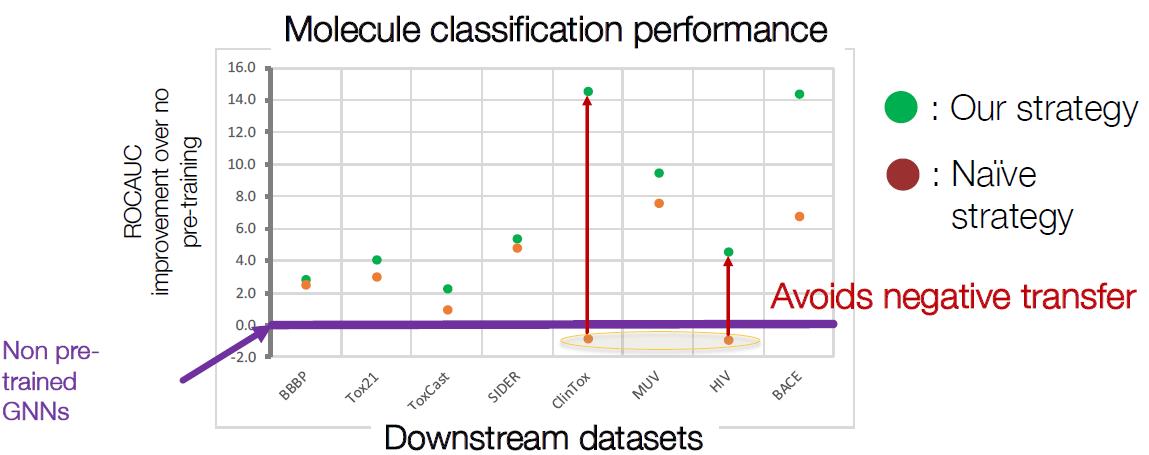
当然，把预训练用在别的模型上也有很大提升，特别是GIN，因为表达能力强的模型能在预训练阶段获取更多的邻域知识，因此提升也最多：

Hyperbolic Graph Embeddings²

常见的GNN任务中，我们通常是将节点或者边的embedding空间假设是${\mathbb{R}}^n$的，但是这个空间一般都是基于欧式距离的，对于一些比较特殊的图结构（满二叉树），这个表示方法会有不足，这节就讨论了如何使用双曲空间来表达GNN的表征。
这节是真有点抽象，光理解概念就有点烧脑。。。

表征空间的选择

上面提到，不同类型的图有不同特点，不一定都适合使用欧氏空间来表征，例如：

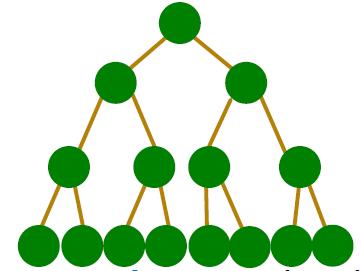
在满二叉树中（树是图的一种特殊形式），每一层的节点都以指数形式在增加，可以看到若干层后，节点之间的距离就太近，以至于欧氏空间无法去区分节点之间的距离，就好比$10^{-99}$与$10^{-100}$两个数字相差10倍，但是太小估计计算机都没有办法区分它们。因此需要使用特殊的空间来进行表征，也是本节研究的重点：双曲空间。
除此之外，还有环形图可以用球形空间：

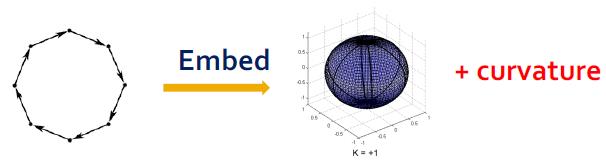
网格图用欧氏空间：

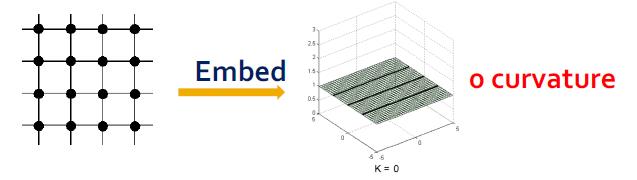
双曲空间模型

双曲空间主要是针对层次化和树形图的，它的好处是可以克服欧氏空间中越来越密集的表征，缺点是现有的DL和优化工具都是针对欧式空间的，对于双曲空间需要额外定义GNN的各种操作。
可以看下b站对双曲空间模型可视化的讲解，比较直观。
双曲空间可视化后等价于Poincaré Model

这个是球不是圆，因此看到这个圆不包含边，在Poincaré Model中每个三角形的面积相等，整个球的半径与$\sqrt{K}$成正比，K是曲率的倒数。
还一种方式就是双曲面模型（Lorentz Model），它是2片双曲面的上片，欧几里德空间的子集。
双曲面模型在数值上是稳定的，而，Poincaré模型需要在Poincaré球的边界附近表示指数级的许多嵌入点。

接下来就是要想办法在双曲空间中表示层次结构的图表征。在这之前，由于没有专门在双曲空间做相关计算的定义，先要给出定义，这里就非常枯燥费脑，粗劣记下把

hyperbolic geometry的相关定义

Manifold: high-dimensional surface
黎曼流形Riemannian Manifold

其内积表示为：$⟨.,.⟩$
内积计算：

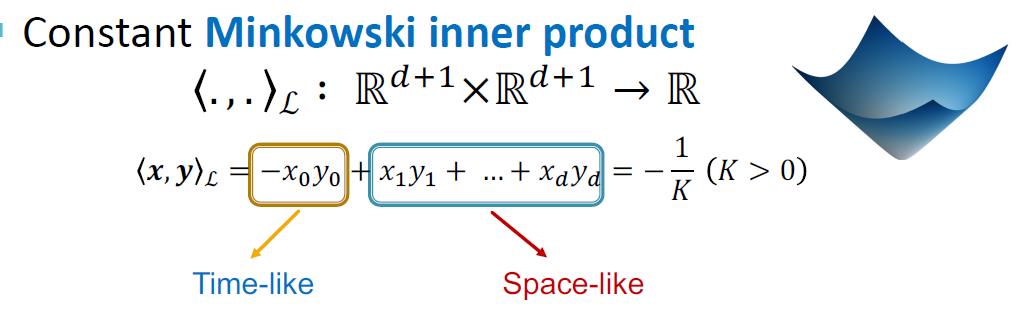
切线空间Tangent space：${\tau }_x$，是流形在任意点$x$处的切线空间，${\mathbb{R}}^n$

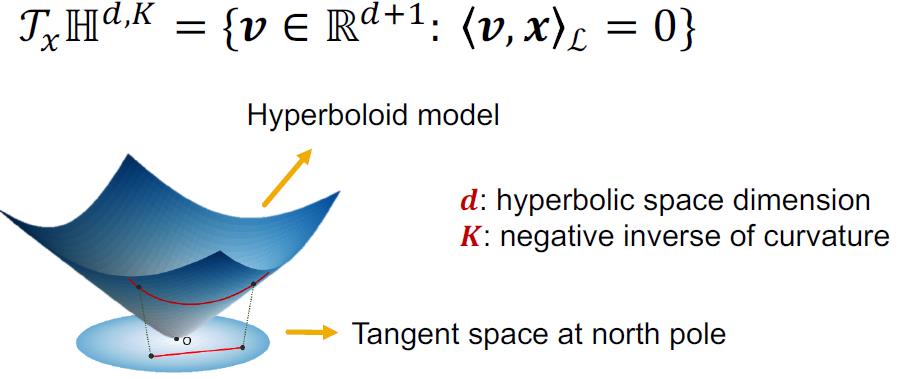
两个函数都是可以导的。
测地线Geodesic：流形中的最短路径，与欧式空间中的直线对应。
双曲空间的测地距离类似于欧氏空间的最短路径距离。

Hyperbolic space是一个带有曲率为$-\frac{1}{K},K>0$的黎曼流形，当$K\to \infty$双曲空间就变成了欧式空间，曲率越小（越负）双曲空间越弯曲，测地线越向内弯曲

双曲空间两点的距离：

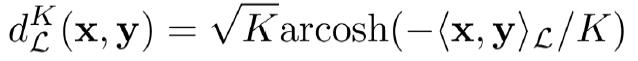
曲率越小（越负），两点距离越增加。

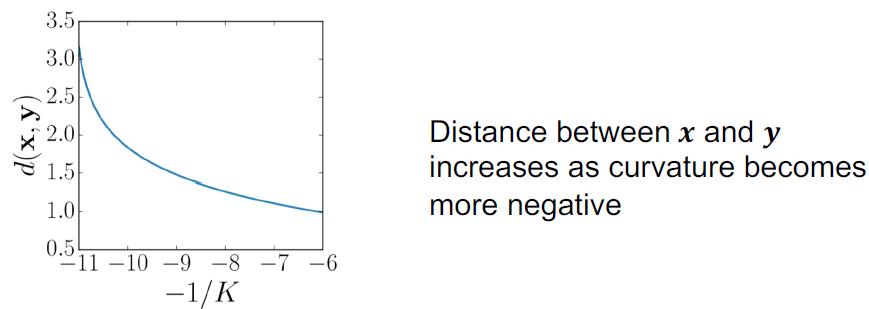
曲率越大，双曲空间对应的Poincare球半径越小，两点之间距离越大。

下面给出双曲空间与欧式空间（切线空间）映射的定义：
Exponential map: from tangent space (Euclidean) to manifold
Logarithmic map: inverse operation of exponential map

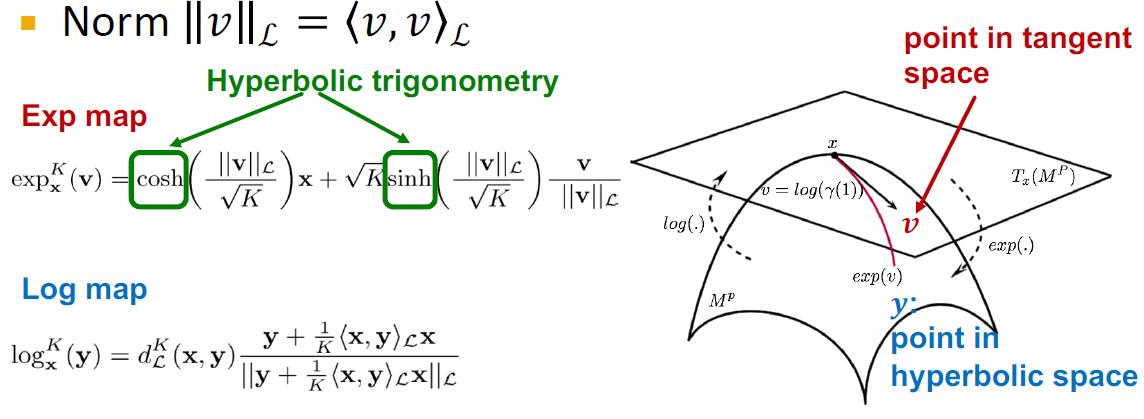
双曲版GNN

前面没看懂没关系，这里也不会看得懂。。。
要玩双曲版GNN有三个难点：
1.输入节点的特征通常是属于欧式空间的
2.如何做双曲版的消息聚合
3.每一层聚合后的结果如何选取合适的曲率来表达
直接给出消息聚合及更新，注意每层GNN对应的双曲空间不一样

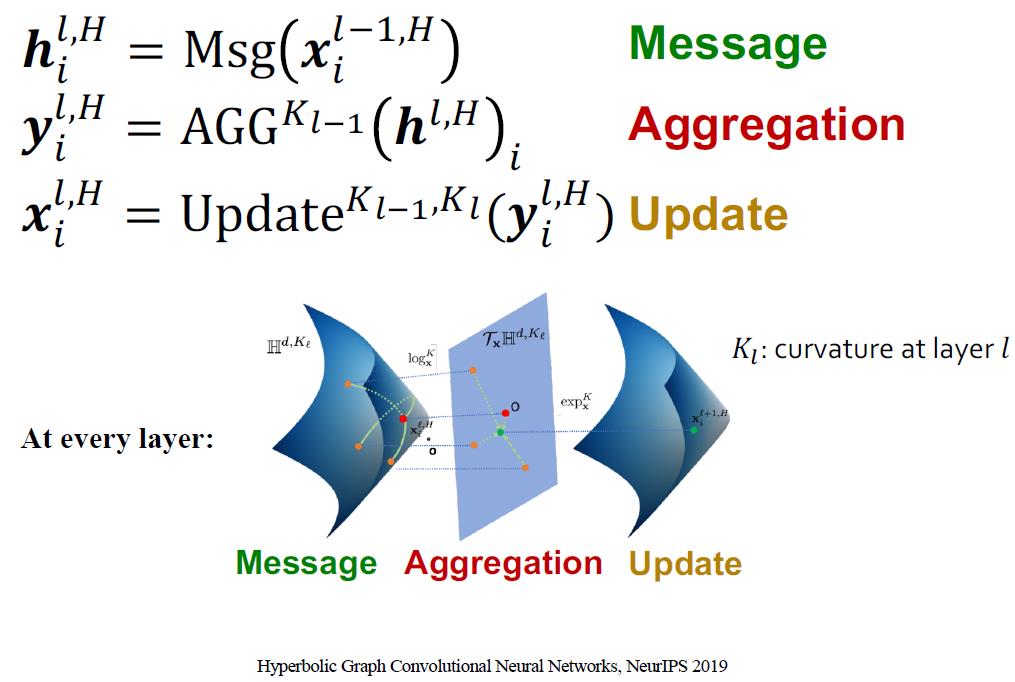
具体公式：

结果

可以看到HGNN对于疾病传播链（可以考虑舆情传播？）有更好的表达：


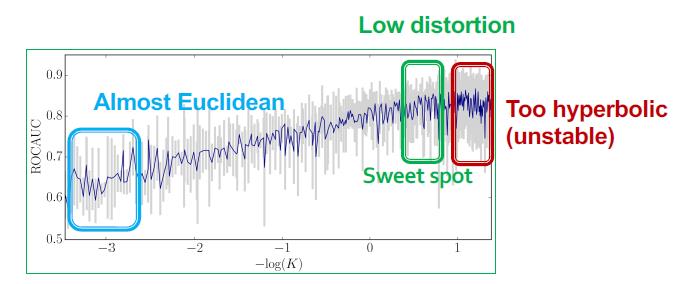
可以看到超参数K非常重要，K太小基本双曲空间退化为欧式空间，ROC不行，太大后可以看到出现不稳定的抖动。

当然，还对非树形或层次的数据集进行了测试。
这里提到使用双曲性hyperbolicity:$\delta$来衡量一个图数据集层次化或树形化程度，$\delta$越小层次化或树形化程度越高，下面是实验对比结果。

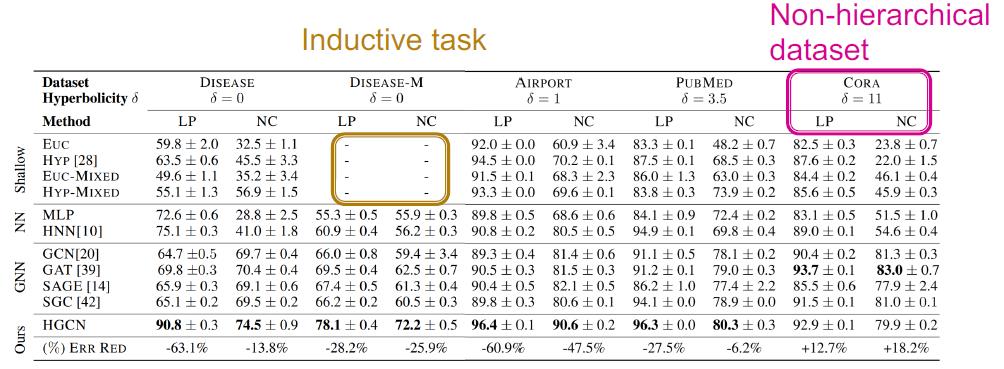
熟悉的CORA没有拿SOTA，其他都拿了。

Design Space of GNN³

这节内容是2020 NeurIPS发的文章，创新性非常高。首次系统研究了GNN的设计空间与任务空间。design space and task space

相关术语

名称	含义	实例
Design	某个具体模型实例	一个4层的GraphSAGE
Design dimensions	模型设计涉及的维度集合	模型的层数 L ∈ { 2 , 4 , 6 , 8 } L\\in\\{2,4,6,8\\} L∈{2,4,6,8}
Design choice	在Design dimension中实际选中的值	$L=2$
Design space	有设计维度进行笛卡尔积得来	层数有4种选择，输出维度有3种选择，则最后的模型种类就有3×4种
Task	某个指定的任务
Task space	由多个任务组成

这里涉及两个我们没有接触过，文章首次提出的概念design space、 task space下面分别讲下：

Design Space

这个分Intra-layer Design和Inter-layer Design
层内设计（单个GNN Layer是什么样子）和层间设计（GNN Layer之间是如何设置）：

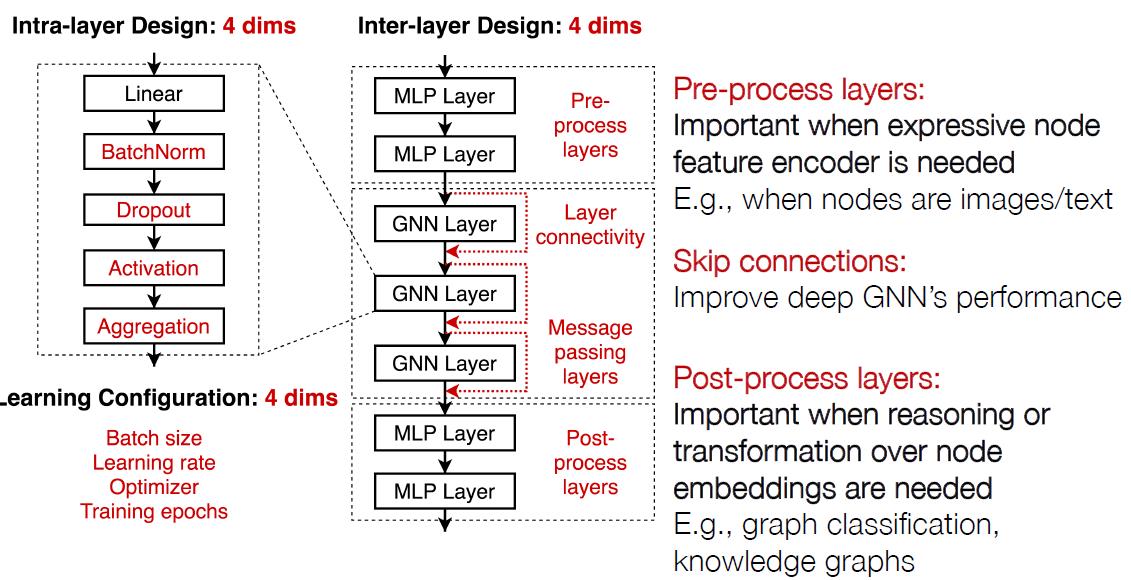
这里面的层内设计涉及4个维度：

维度名称	常见取值
Batch normalization	True. False
Dropout	False， 0.3，0.6
Activation	RELU， PRELU， SWISH
Aggregation	MEAN，MAX， SUM

层间设计也有4个维度

维度名称	常见取值
Pre-process layers	1,2,3
Layer connectivity	STACK, SKIP-SUM, SKIP-CAT
Message passing layers	2,4,6,8
Post-precess layers	1,2,3

模型的Learning configurations（超参数）

维度名称	常见取值
Batch size	16,32,64
Learning rate	0.1,0.01,0.001
Optimizer	SGD,ADAM
Training epochs	100,200,400

做DL的都知道，一超参数般都是靠经验来选，当然有些参数做网格搜索，它们对于性能的影响很大。
把上面的各种可能进行排列组合共有31.5万种可能。
当然，这里如果还要考虑模型的细节，例如是否添加注意力机制，添加几头什么的，没有加进来，文章的目标不是考虑所有的GNN可能的设计，而是想要表明研究design space比起单个模型优化而言更加有效。言外之意就是说花大心思去搞什么花里胡哨的模型，还不如扎实的落实好基本的模型设计，性能提升更加明显。

Task Space

一提到GNN的任务，那基本就是：node / edge / graph level task，虽然这个分类很合理，但是不够精确，毕竟不能量化，例如：都是节点级别的预测：预测聚集系数与预测节点的主题区域却是两个不同的任务。而且这样的分类方法比较主观。这个文章提出了一种量化任务的方式：
1.选择若干个锚点模型（这里以5个为例）：$M_1,\cdots ,M_5$
2.用锚点模型对某个任务的性能排序作为该任务的特征
3.排序特征相近的任务相似性越高
例如：

从上表中可以看到任务A与B比较相似，而A与C不相似。
由于不同模型对不同数据集的性能不一样，如何确定锚点模型才不会使得锚点模型过于集中于某个类型的模型？这里给出大概的步骤，基本思想就是以一个数据集为衡量标准，然后取各种性能的模型作为锚点模型：
1.选择一个小的数据集，例如Cora做节点分类
2.从design space中随机采样$N$个模型，并且将他们在数据集上分别跑一次，假设这里$N=100$
3.将上一步得到结果进行排序，并根据排序选出$M$个模型作为锚点模型，如果选5个，那么就是选排名为1,25,50,75,100的，这样避免扎堆选。原文选了12个。
回到刚才的主题，任务空间，弄了32个任务：node / graph classification

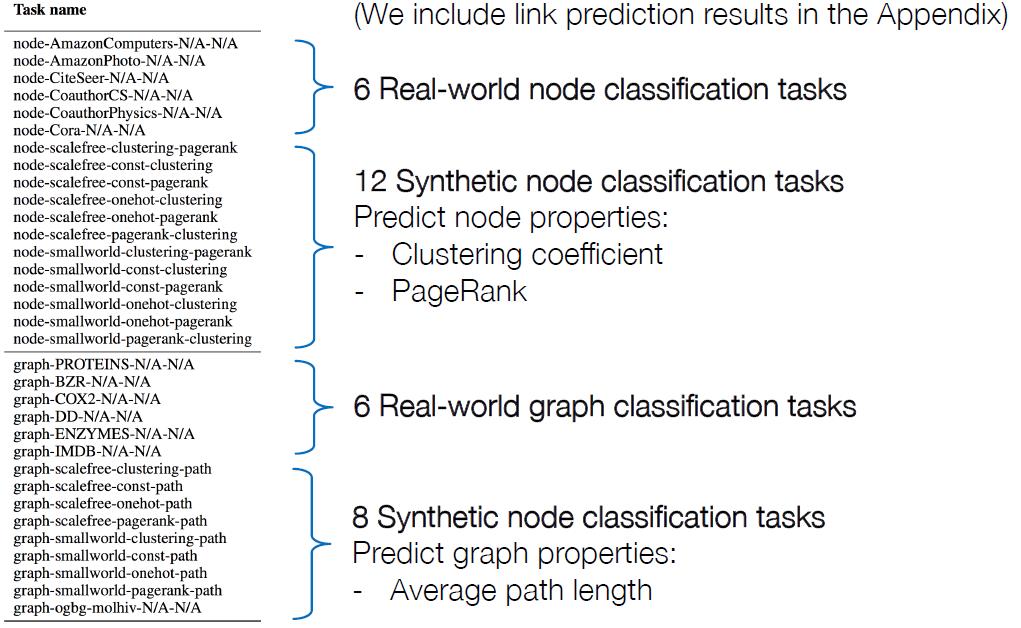
模型的评估

主要是指对模型的某一个design dimension进行评估，这里以是否加BatchNorm为例进行说明。
传统的做法是：
1.选一个模型，例如一个5层64维的GCN
2.将BatchNorm分别设置为True / False在模型上跑一组

而本文中，我们可选择的模型×任务组合越有1000万（31.5万个模型×32任务），具体做法如下：
1.从1000万个模型×任务组合采样若干个组合
2.将这些组合分别在atchNorm设置为True / False的条件下各来一下，并将各组结果进行排序。
为了使得结果更加有说服力，文中专门为评估设计了一个算法：controlled
random search

controlled random search

翻译过来是受控随机搜索，具体做法：
1.随机采样模型×任务的组合，并将BatchNorm = [True, False]分配给这些组合，例如：

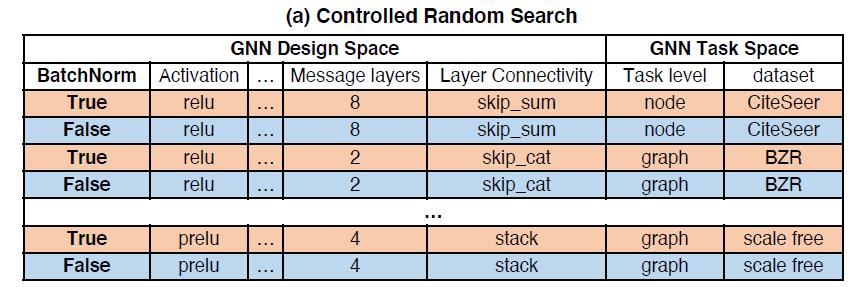
2.将BatchNorm = [True, False]的性能结果进行排序，值越小性能越好：

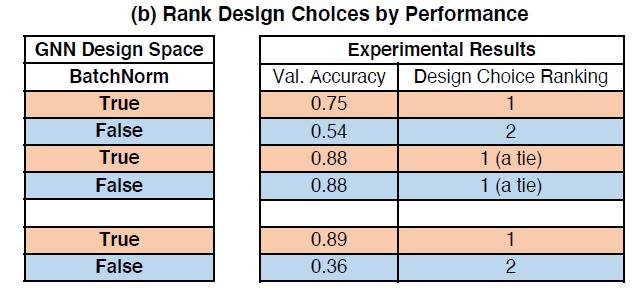
3.将BatchNorm = [True, False]的均值/排序的分布画出来：

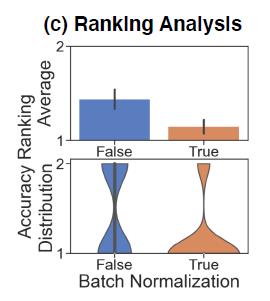
可以利用相同的方法来评估任意一个新的模型design dimension，例如增加一个新的GNN层是否会有好效果。

实验结果1：GNN设计指南

根据上面的方法对一些design dimension进行了评估，给出了一些GNN设计建议，先看层内设计：

维度名称	结果	解释
Batch normalization		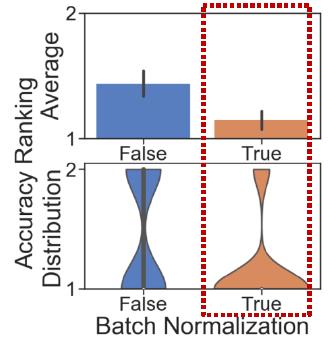GNN模型比较难以优化，因此加BN会对性能有提升
Dropout		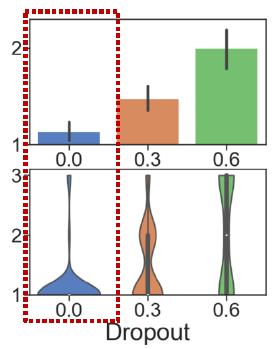GNN通常是出现欠拟合，而抓爆是针对过拟合优化，实验表明大多数情况没有必要使用抓爆
Activation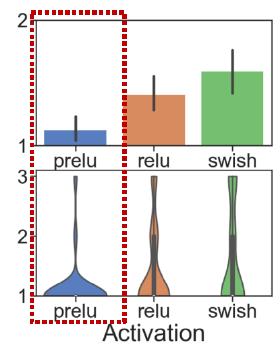
Aggregation		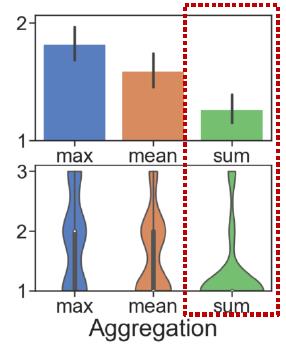之前有讲过GNN的聚合函数表现能力，SUM是这三个里面最强的

PReLU(Parametric Rectified Linear Unit)，是带参数的ReLU，何凯明15年提出的，这里是新发现，这里使用PReLU做激活函数效果最好。

接下来的是层间设计相关维度，这里不画表了，简单说下：

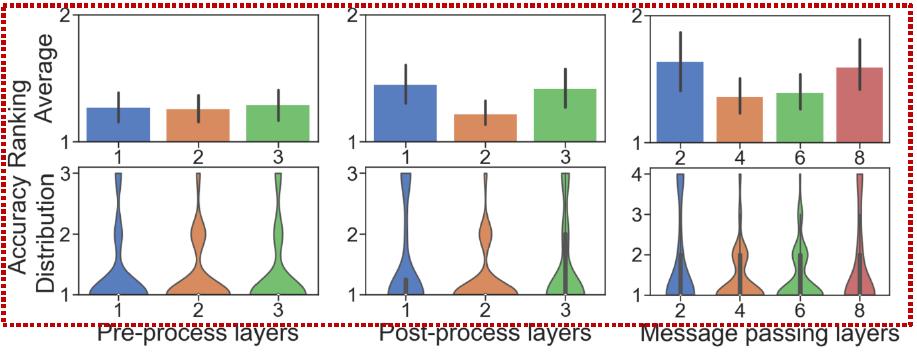
Pre-process layers、Post-precess layers、Message passing layers这三个维度没有很明显的选择差异，他们三个和特定任务有关；

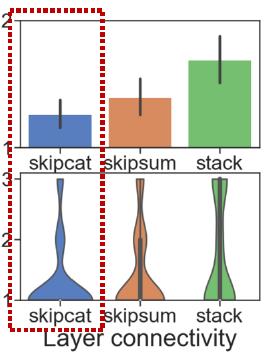
Layer connectivity维度从上图中可以看到采用SKIP-CAT（残差方式连接）效果最好（残差方式可以有助于层次化的节点表达）

最后是模型的Learning configurations（超参数）设计：

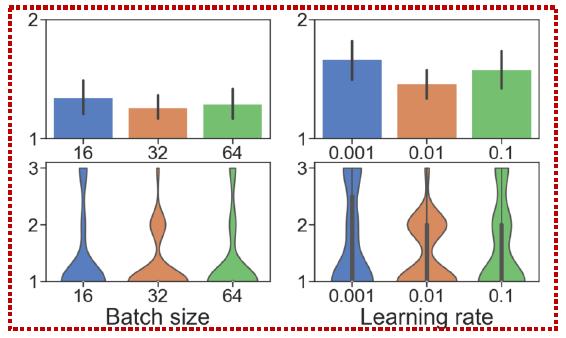
上图表示Batch size、Learning rate的选择和任务高度相关。

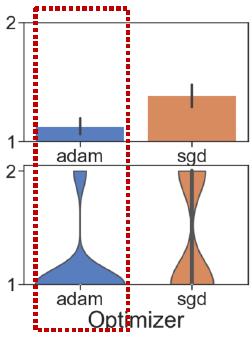
上图则表明优化器还是选ADAM有较好的鲁棒性。

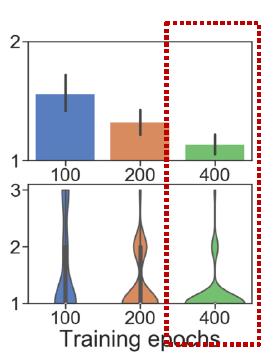
最后就是训练的epoch，越多越好。

实验结果2：理解GNN相关任务

从前面结果可以看到，不同的任务最优的GNN模型设计大不一样（尤其是提到的几个和任务相关性较强的维度，例如下面的Aggregation，消息传递层数）。下图给出几个不同任务，在什么参数下最好：

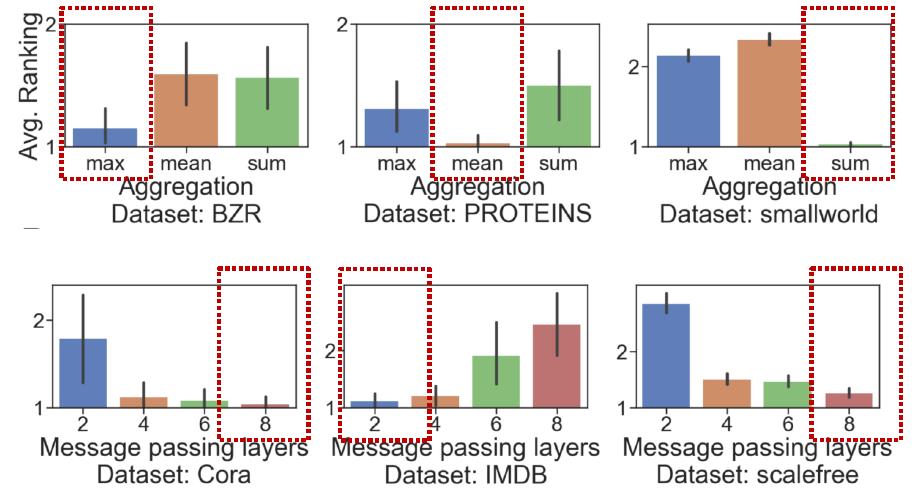
因此理解task space很关键。把前面的计算任务相似度的算法拿来，把32个任务两两之间相似度可视化，就构造了GNN的task space：

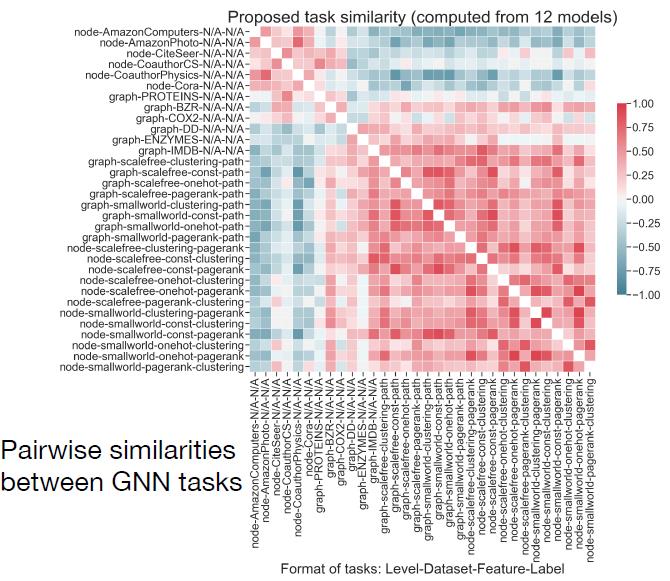
从可视化结果分析，文中提出的32个任务组成的task space非常有代表性，可以分为两组：

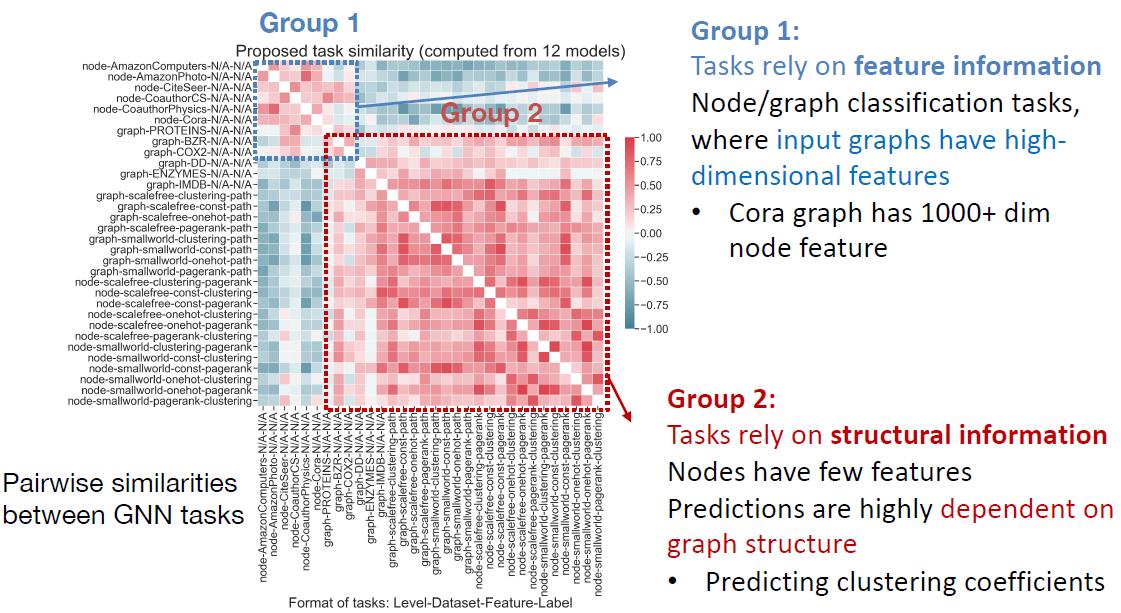
组1是有丰富特征信息的，那么任务会依赖特征信息一些；
组2是没有什么特征信息的，那么任务会依赖图本身的结构信息多一些。
进一步把上面的任务的特征（用12个model跑出来的性能排序组成）降维显示：

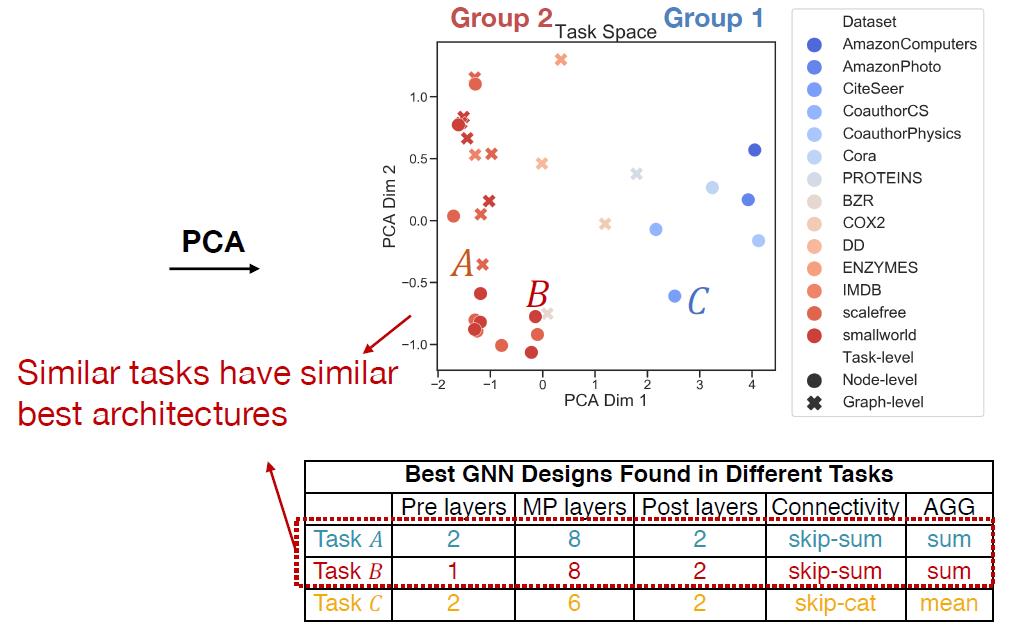
得到的结论是相似任务的最优GNN 模型设计也非常相似。

实验结果3：设计迁移

如何将任务空间学习到的模型最优构架信息泛化到没有看见过的任务上？
这里做了一个实验，对OGB的ogbg-molhiv数据集⁴看生成最优模型效果，这个数据集与现有32个数据集完全不一样，20倍大，样本不平衡（只有1.4%正样本），并且需要out-of-distribution的泛化性。
步骤再重复一遍：
1.用12个锚点模型对ogbg-molhiv数据集跑一遍；
2.计算上一步结果与32个现有数据集的相似性

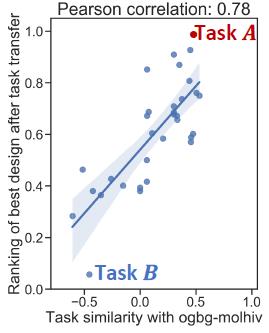
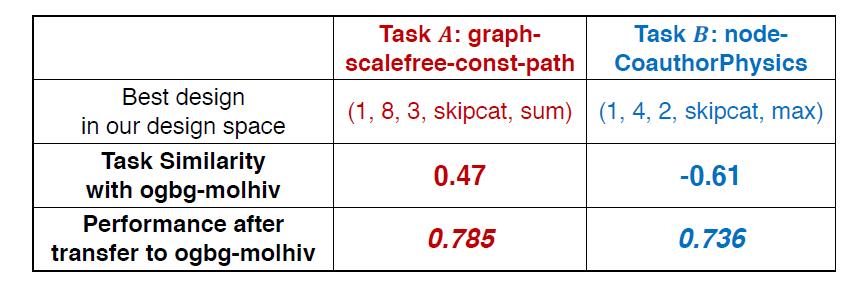
3.从现有任务中获得最佳模型构架设计。
从步骤2中得到两个结果，一个最优一个最差，然后将最优结果任务A的最优模型迁移到OGB上，比原来SOTA（0.771）还牛。。。

---

1. Strategies for pre-training graph neural networks ↩︎

2. Hyperbolic Graph Convolutional Neural Networks ↩︎

3. Design Space for Graph Neural Networks ↩︎

4. Open Graph Benchmark:Datasets for Machine Learning on Graphs ↩︎