[LNOI2014]LCA（树链剖分）

Posted 2021-11-11 吃花椒的妙酱

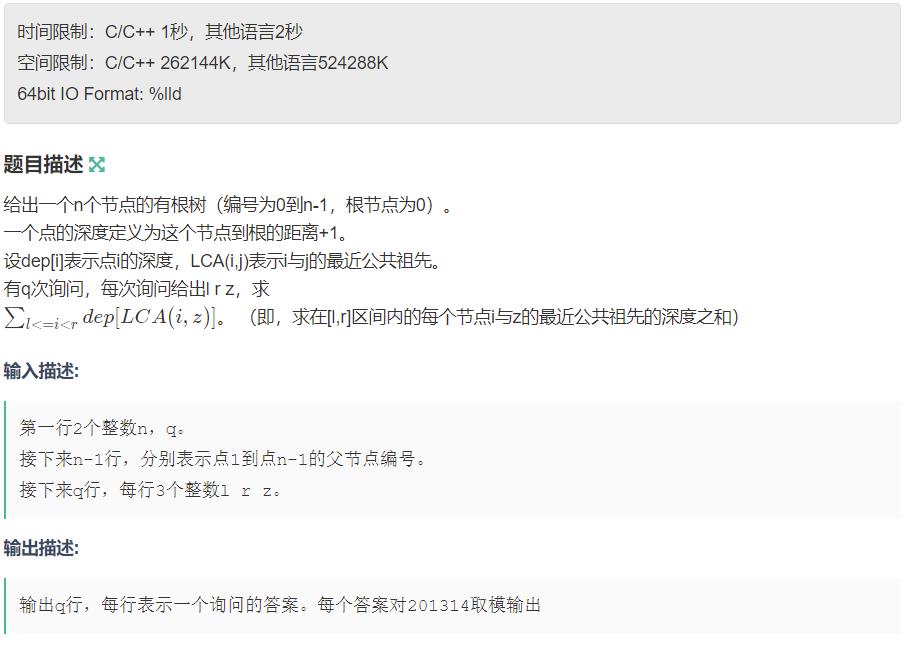
思路：先考虑dep有什么性质，dep定义是深度即根到节点的长度。由lca性质，我们知道，对于[l,r]区间里的任意i，它与z的lca一定是z的祖先或者z自己，。

考虑i对lca的dep的贡献，我们把i到根的路径上的所有结点+1，对区间所以i操作完后，dep之和即为z到根路径上的权值和。

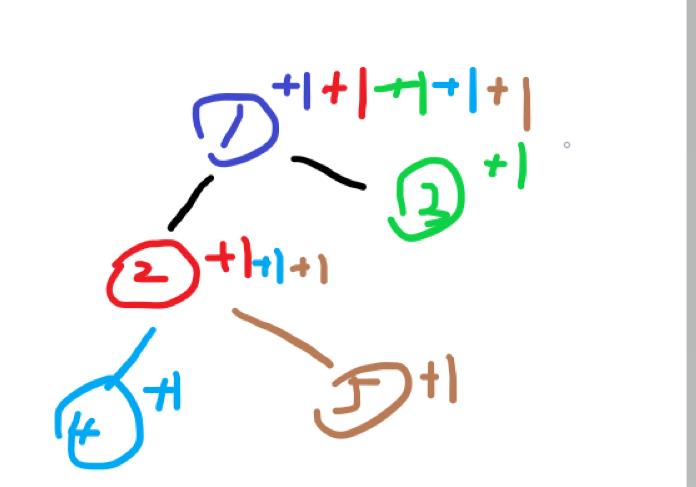
假设我对[1,5]区间这样操作后，求z=5时的答案，即为1,2,5的权值和。树链剖分后用线段树维护，即可在O(n*logn*logn)内实现一次询问，但是每次这样操作后需要清空线段树，何况有q次询问，直接tle了。

考虑询问离线，对于询问[l,r]，等价于[1,r]的答案[1,l-1]答案，询问差分后，按照右端点排序后离线处理维护即可，只有加值无需删点。

或者用主席树实现在线，下面是离线版代码。 

关键还是第一步dep含义的转化吧，比较核心

#define _CRT_SECURE_NO_WARNINGS
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <map>
#include <list>
#include <queue>
#include <vector>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <deque>
#include <set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define scd(v) scanf("%d",&v)
#define scdd(a,b) scanf("%d %d",&a,&b)
#define endl "\\n"
#define IOS ios::sync_with_stdio(false),cin.tie(0)
#define pb push_back
#define all(v) v.begin(),v.end()
#define mst(v,a) memset(v,a,sizeof(v))
#define ls p<<1
#define rs p<<1|1
#define int long long
#define inf 0x7f7f7f7f
#define fi first
#define se second
#define pii pair<int , int >
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
const int N = 5e4 * 4 + 10;
const int mod = 201314;
int n, m;
int fa[N], son[N], a[N];
int tr[N << 2], lz[N << 2];
int st[N], ed[N], dfn, dep[N], siz[N], top[N];
int id[N], b[N];
vector<int > G[N];
struct Q//询问离线
{
    int ti, op, id,ans;
    bool operator < (const Q& t) const//按照右端点排序
    {
        return ti < t.ti;
    }
}q[N<<1];
void pushup(int p)
{
    tr[p] = (tr[ls] + tr[rs]) % mod;
}
void pushdown(int p, int l, int r)
{
    int x = lz[p]; lz[p] = 0;
    int mid = (l + r) >> 1;
    int llen = mid - l + 1;
    int rlen = r - mid;
    lz[ls] = (lz[ls] + x) % mod, lz[rs] = (lz[rs] + x) % mod;

    tr[ls] = (tr[ls] + x*llen) % mod, tr[rs] = (tr[rs] + x*rlen) % mod;
    
}
void update(int p, int l, int r, int x, int y, int val)
{
    if (x <= l && r <= y)
    {
        int len = r - l + 1;
        tr[p] = (tr[p] + len*val)%mod;
        lz[p] += val;
        return;
    }
    if ( lz[p]!=0 ) pushdown(p, l, r);
    int mid = (l + r) >> 1;
    if (x <= mid) update(lson, x, y, val);
    if (y >= mid + 1) update(rson, x, y, val);
    pushup(p);
}
int query(int p, int l, int r, int x, int y)
{
    if (x <= l && r <= y)
    {
        return tr[p];
    }
    if (lz[p]!=0) pushdown(p, l, r);
    int mid = (l + r) >> 1;
    ll res = 0;
    if (x <= mid)res = query(lson, x, y);
    if (y >= mid + 1) res += query(rson, x, y);
    return res;
}
void dfs1(int x, int f)
{
    dep[x] = dep[f] + 1;
    fa[x] = f;
    siz[x] = 1;
    for (int y : G[x])
    {
        if (y == f) continue;
        dfs1(y, x);
        siz[x] += siz[y];
        if (!son[x] || siz[y] > siz[son[x]]) son[x] = y;
    }
}
void dfs2(int x, int tp)
{
    id[x] = ++dfn;
    b[dfn] = a[x];
    top[x] = tp;
    if (son[x]) dfs2(son[x], tp);
    for (int y : G[x])
    {
        if (y == fa[x] || y == son[x]) continue;
        dfs2(y, y);
    }
}
void de()
{
    cout << " b[] " << endl;
    _for(i, 1, n) cout << b[i] << " ";
    cout << endl;

    cout << " id[] " << endl;
    _for(i, 1, n) cout << id[i] << " ";
    cout << endl;

    cout << " top[] " << endl;
    _for(i, 1, n) cout << top[i] << " ";
    cout << endl;

    cout << " son[] " << endl;
    _for(i, 1, n) cout << son[i] << " ";
    cout << endl;
}
void add(int ti)
{
    int x = ti;
    while (top[x] != 1)
    {
        update(1, 1, n, id[top[x]], id[x], 1);
        x = fa[top[x]];
    }
    update(1, 1, n, id[1], id[x],1);
    return;
}
int QQ(int x)
{
    int ans = 0;
    while (top[x] != 1)
    {
        ans += query(1, 1, n, id[top[x]], id[x]) , ans%=mod;
        x = fa[top[x]];
    }
    ans += query(1, 1, n, id[top[x]], id[x]) , ans %=mod;
    return ans ;
}
bool cmp(Q x, Q y)
{
    if (x.id != y.id) return x.id < y.id;
    return x.ti < y.ti;
}
void solve()
{
    //预处理树上信息
    dfs1(1, 0);
    dfs2(1, 1);
    sort(q + 1, q + 1 + 2*m);//询问离线
    int ti = 0;//区间时间轴
    _for(i, 1, 2*m)
    {
        while (ti < q[i].ti)
        {
            add(++ti);//需要加点
        }
        q[i].ans = QQ(q[i].op);//处理询问
    }
    sort(q + 1, q + 1 + 2 * m, cmp);//还原询问
    for (int i = 1; i <= 2 * m; i += 2)
    {
        cout << (q[i + 1].ans - q[i].ans + mod) % mod<<endl;
    }
}
signed main()
{
  //  freopen("data.txt","r",stdin);
    IOS;
    cin >> n >> m;
    _for(i, 2, n )
    {
        int x; cin >> x;
        x++;
        G[i].push_back(x);
        G[x].push_back(i);
    }
    _for(i, 1, m)
    {
        int l, r, x;
        cin >> l >> r >> x;
        l++, r++, x++;//因为从0开始，全部+1方便维护
        //询问差分
        q[i].ti = l-1;
        q[i].op = x;
        q[i + m].ti = r;
        q[i + m].op = x;
        q[i].id = q[i + m].id = i;
    }
    solve();
    AC;
}