数据结构和算法超多图解,超详细,堆详解
Posted Linux猿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构和算法超多图解,超详细,堆详解相关的知识,希望对你有一定的参考价值。
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏:图解数据结构和算法 (优质好文持续更新中……)🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录
🍓一、什么是堆
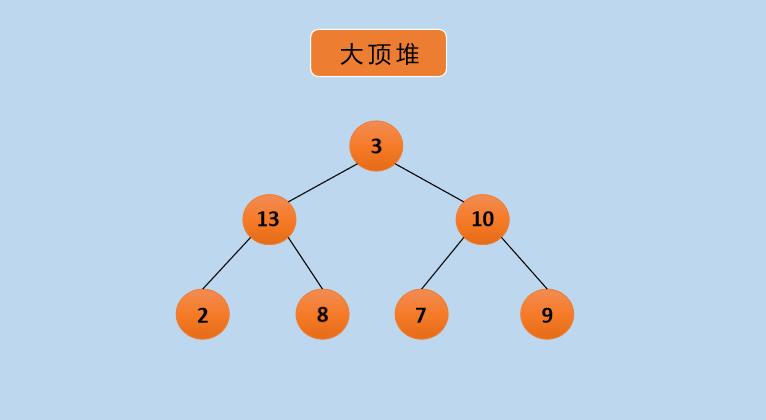
堆属于二叉树的一种,它是一棵完全二叉树。堆有大顶堆和小顶堆之分,大顶堆是任意节点大于其左右子节点,小顶堆是任意节点大于其左右子节点,如下所示:

在上图中,每个节点的值都大于左右孩子节点的值,例如:25 大于 13 和 10,13 大于 2 和 8 等。
使用上面的数据来构建一个小顶堆,如下所示:
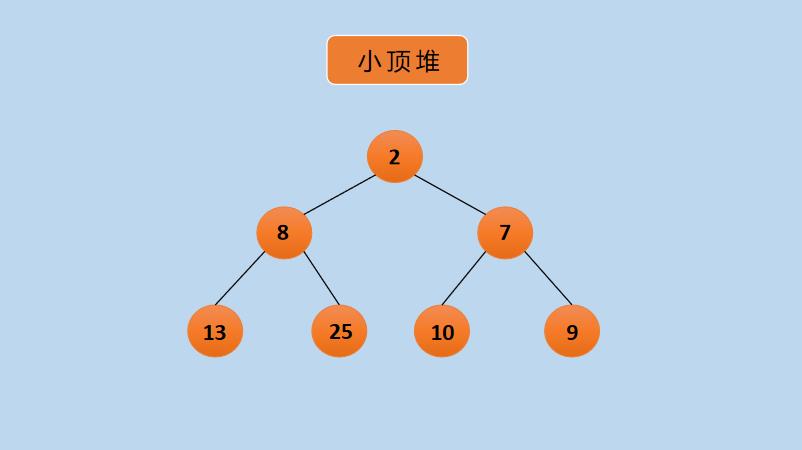
在上图的小顶堆中, 每个节点都小于左右孩子节点,左右孩子节点谁大谁小并没关系,重点是不能比父节点大,可以看到,2 比孩子节点 8 和 7 都小,8 比孩子节点 13 和 25 都小。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓二、堆排序
这里以大顶堆为例进行讲解。
✨2.1 算法原理
将待排序元素组成一个大顶堆,每次取出堆顶元素(堆顶是最大的元素),让最后一个元素成为堆顶节点,重新调整堆,让其成为大顶堆,再次交换堆顶元素,直到所有元素都有序,从而实现对数据的排序。
✨2.2 算法步骤
(1)将待排序元素构建一个大顶堆;
(2)最后一个节点与根节点交换,此时,不再是大顶堆;
(3)将堆重新调整堆为大顶堆;
(4)重复步骤 2 ~ 3,直到所有元素都有序。
✨2.3 实例演示
下面来看一个实例。
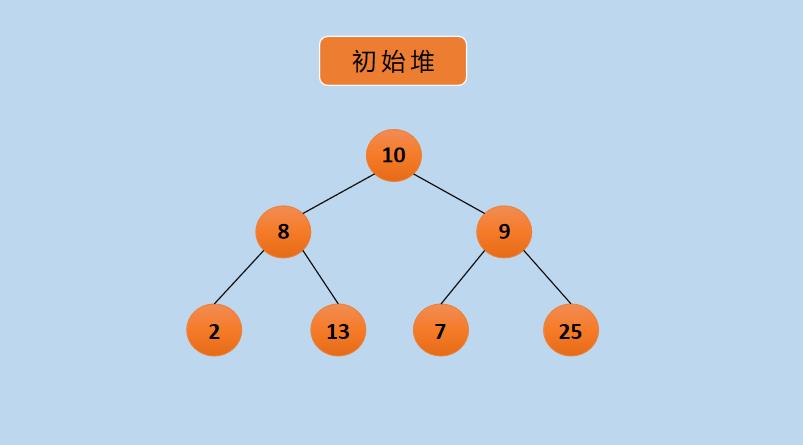
假设有 A[ ] = {10, 8, 9, 2, 13, 7, 25},这里以大顶堆为例实现从小到大排序。
(1)初始堆,如下所示:
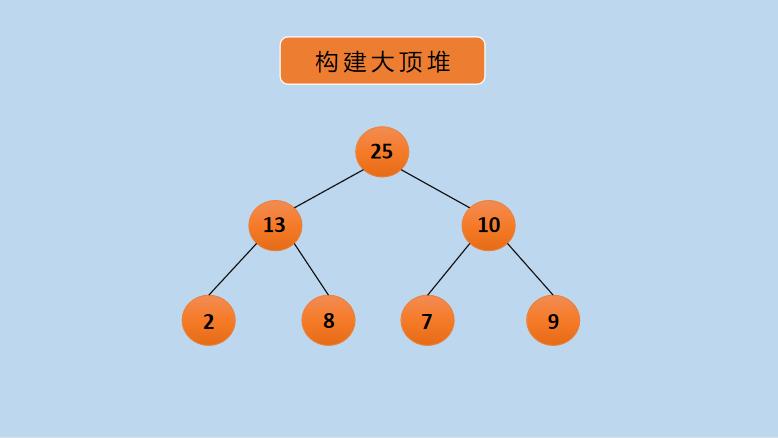
(2)将待排序元素构建成一个大顶堆,如下所示:
(3)将节点 9 与 节点 25 交换,交换后如下所示:

(4)标记为红色的节点表示已经有序,不再参与排序,这时候,堆不满足大顶堆,重新调整堆为大顶堆,调整后如下所示:

(5)将节点 13 与 7 交换,交换后,如下所示:
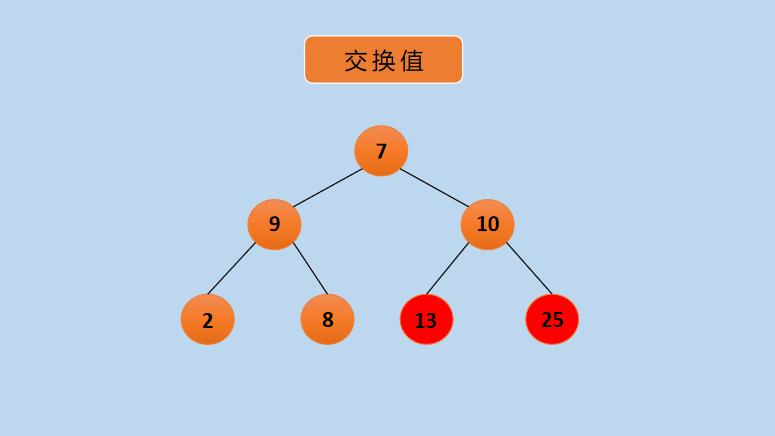
(6)交换后,此时的堆不再是大顶堆,重新调整为大顶堆,调整后如下所示:

(7)交换节点 10 与 8,交换后如下所示:

(8)此时堆不再是大顶堆,重新调整为大顶堆,如下所示:
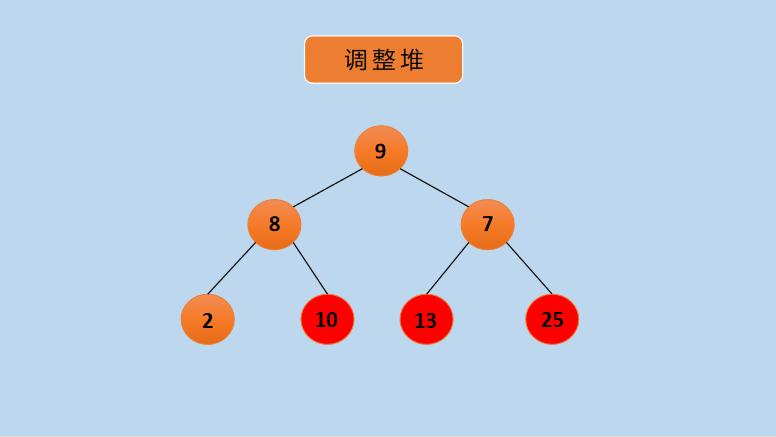
(9)交换节点 9 和 2,交换后,如下所示:
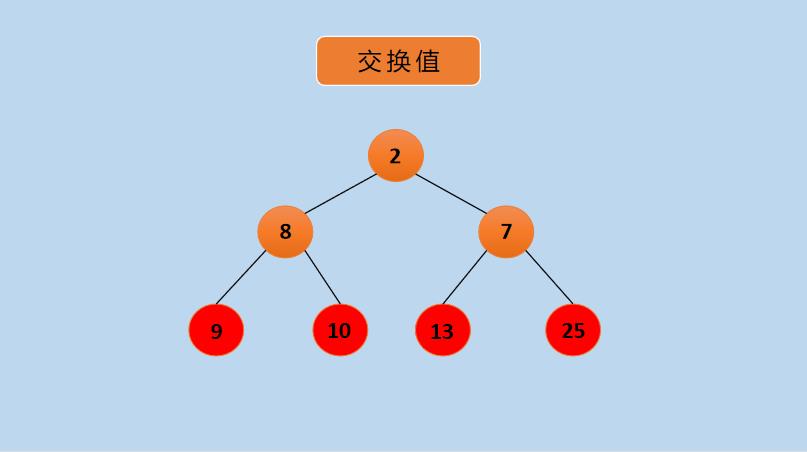
(10)将堆重新调整为大顶堆,如下所示:
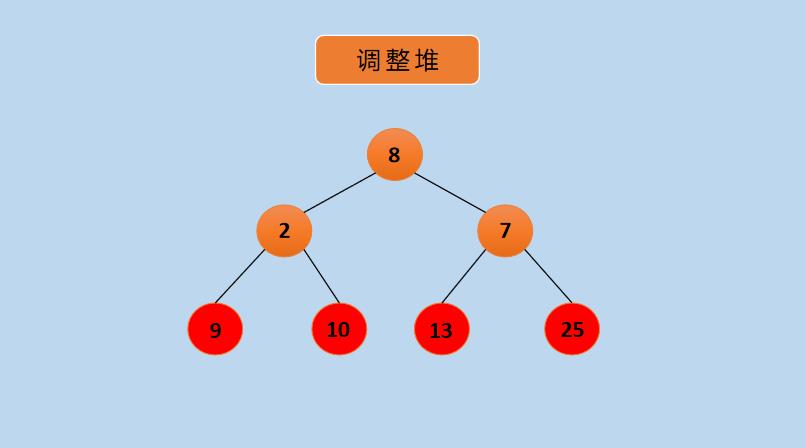
(11)交换 8 和 7 的值,如下所示:
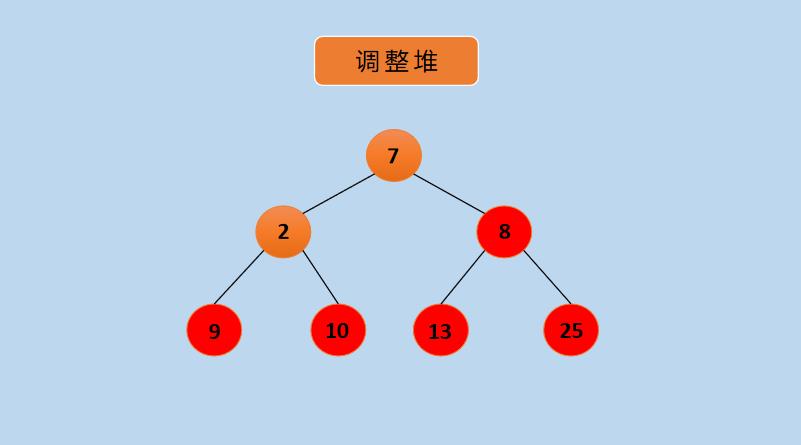
(12)将堆调整为大顶堆,可以看到,当前堆已是大顶堆,然后,交换节点 2 和 7,如下所示:

(13)此时,整个对从上到下,从左到右是递增的,实际在数组中存储是这样的:
在上图中,节点下面的数字表示节点在数组中的位置,一般是从下标 1 开始存储,因为这样方便计算父节点和子节点之间的关系,如下所示:
(1)左孩子节点的下标 = 父节点的下标 * 2
(2)右孩子节点的下标 = 父节点的下标 * 2 + 1
✨2.4 代码实现
#include <iostream>
using namespace std;
//向下调整堆, 从 idx 节点开始往下调整
void adjustHeap(int a[], int idx, int Len){
while(idx*2+1 < Len) {
int temp = idx*2 + 1;
if(temp+1 < Len && a[temp+1] > a[temp]) {
temp++;
}
if(a[idx] < a[temp]) {
swap(a[idx], a[temp]);
idx = temp;
} else break;
}
}
/*
* 堆排序
* g[] : 待排序数组
* n : 元素个数
*/
void heapSort(int g[], int n){
//先建立大顶堆
for(int i = (n-1)/2; i >= 0; --i){
adjustHeap(g, i, n);
}
//排序,每次都会有一个元素有序
for(int i = 0;i < n; ++i){
swap(g[0], g[n-i-1]);
adjustHeap(g, 0, n-i-1);
}
}
int main()
{
int n = 8;
int g[] = {5, 7, 9, 3, 1, 8, 6, 2};
heapSort(g, n); // 调用堆排序
for(int i = 0; i < n; ++i) {
cout<<g[i]<<" ";
}
cout<<endl;
return 0;
}在堆排序的过程中,重点是调整堆,建立大顶堆的时候(heapSort 中第一个 for 循环),是从下往上依次调整每个节点,使得每个节点都满足大顶堆的条件。
正式排序的时候,每次只需要交换根节点,重新调整堆即可,只需要调整新的根节点,因为只有新的根节点不满足堆的定义。
✨2.5 堆调整原理
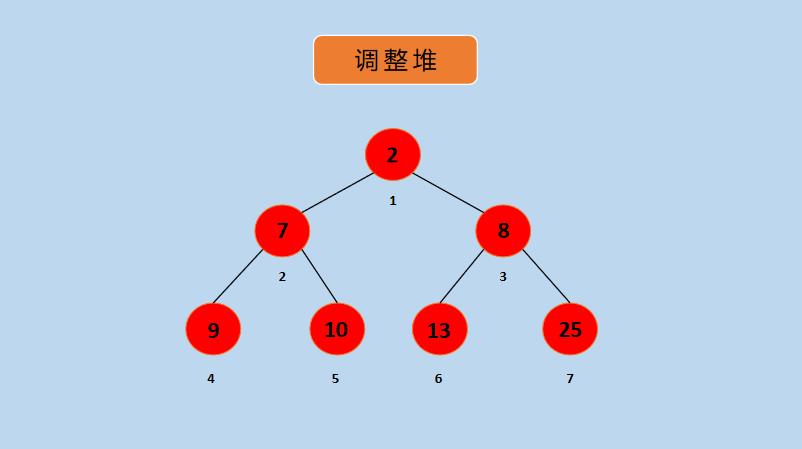
堆排序中,最重要的就是堆的调整了,下面就可以下图的为例子进行讲解,如下所示:
在上图中,只有 3 是不符合条件的,下面就来调整下 3 节点,动图如下所示:

在上图中,3 先与 13 交换,然后,再与 8 交换,交换后便成为一个大顶堆。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓三、实例讲解
✨3.1 求第 k 大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
🚩3.1.1 算法思路
对数组 nums 中的元素进行堆排序,因为堆排序可以每次确定一个最大值,所以只需要求解到第 k 个最大值即可。如果使用其它排序算法,要排序所有元素,这就显示出了堆排序的优势,并不需要全部排序完才找到第 k 大的元素。
🚩3.1.1 代码实现
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
//向下调整堆
void adjustHeap(vector<int>& nums, int idx, int Len) {
while(idx*2+1 < Len) {
int temp = idx*2 + 1;
if(temp + 1 < Len && nums[temp+1] > nums[temp]){
temp++;
}
if(nums[idx] < nums[temp]) {
swap(nums[idx], nums[temp]);
idx = temp;
} else break;
}
}
int findKthLargest(vector<int>& nums, int k) {
//先建立大顶堆
int n = nums.size();
for(int i = (n-1)/2; i >= 0; --i){
adjustHeap(nums, i, n);
}
for(int i = 0; i < nums.size(); ++i) {
cout<<nums[i]<<" ";
}
cout<<endl;
//排序
for(int i = 0;i < k - 1; ++i){
swap(nums[0], nums[n-i-1]);
adjustHeap(nums, 0, n-i-1);
}
return nums[0];
}
};
int main()
{
int g[] = {5, 7, 9, 3, 1, 8, 6, 2};
vector<int> nums(g, g+8);
cout<<endl;
Solution obj;
int k;
while(cin>>k) {
cout<<"The k-th largest number is "<<obj.findKthLargest(nums, k)<<endl;
}
return 0;
}
✨3.2 求前 k 高频率的元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按任意顺序 返回答案。
🚩3.2.1 算法思路
这个题目类似于第一个题目,但是需要计算每个整数的频率,可以使用 map 进行统计,然后就可以使用堆排序求第 k 大了。
🚩3.2.2 代码实现
#include <iostream>
#include <vector>
#include <map>
using namespace std;
class Solution {
public:
//向下调整堆
void adjustHeap(vector<pair<int, int> >& nums, int idx, int Len) {
while(idx*2+1 < Len) {
int temp = idx*2 + 1;
if(temp + 1 < Len && nums[temp+1].second > nums[temp].second){
temp++;
}
if(nums[idx].second < nums[temp].second) {
swap(nums[idx], nums[temp]);
idx = temp;
} else break;
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
map<int, int>mp;
for(int i = 0; i < (int)nums.size(); ++i) {
mp[nums[i]]++;
}
vector<pair<int, int> >hep;
map<int, int>::iterator it;
for(it = mp.begin(); it != mp.end(); ++it) {
hep.push_back(pair<int, int>(it->first, it->second));
}
//先建立大顶堆
int n = hep.size();
for(int i = (n-1)/2; i >= 0; --i){
adjustHeap(hep, i, n);
}
//排序
vector<int> ans;
for(int i = 0;i < k - 1; ++i){
ans.push_back(hep[0].first);
swap(hep[0], hep[n-i-1]);
adjustHeap(hep, 0, n-i-1);
}
ans.push_back(hep[0].first);
return ans;
}
};
int main()
{
int g[] = {1, 2, 2, 1, 3, 8, 8, 1};
vector<int> nums(g, g+8);
cout<<endl;
Solution obj;
int k;
while(cin>>k) {
vector<int> ans = obj.topKFrequent(nums, k);
for(int i = 0; i < ans.size(); ++i) {
cout<<ans[i]<<" ";
}
cout<<endl;
}
return 0;
}
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓四、总结
堆排序经常用在求第 K 大上,因为堆的每次调整,根元素一定是最大/小的元素。

欢迎关注下方👇👇👇公众号👇👇👇,获取更多福利等你来领🤞(比心)!
以上是关于数据结构和算法超多图解,超详细,堆详解的主要内容,如果未能解决你的问题,请参考以下文章