python进行数据预处理（最大最小值规范化零均值规范化剔除奇异值去噪曲线拟合）小白互懂文qwq

Posted 2021-11-11 晴一千天

博主此次数据挖掘作业是对数据进行预处理练习，我也是第一次接触并也是上网查阅资料完成，此篇文章算是作业总结，作为小白代码有冗余的地方，不足之处请海涵，欢迎斧正。

数据是mat文件——MATLAB存储数据的标准文件格式，在MATLAB中打开显示类似于单行EXCEL表格。由于本人水平较次，对python更熟悉些，就不用matlab做，而用python。

目录

1.需要调用的库

2.读取mat文件中数据 

mat文件链接：

3.最大最小值规范化、零均值规范化代码实现

规范化后图形展示

 代码中部分函数简介：

4.剔除奇异值和去除高斯噪声代码实现

代码中部分函数简介：

结果运行展示：

附加——拟合剔除奇异值、去噪后的曲线： 

5.感谢申明

---

1.需要调用的库

import numpy as np
import scipy.io
import copy
import matplotlib.pyplot as plt

NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库；Scipy库是基于python生态的一款开源数值计算，科学与工程应用的开源软件；copy库用来拷贝数据；Matplotlib 是一个 Python 的 2D 绘图库，它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形，用来可视化数据。

2.读取mat文件中数据 

mat文件链接：

链接：https://pan.baidu.com/s/1hjDSHHwgcxdcTM3yFfQ0cw 
提取码：0530

datafile = 'E:\\\\pycharm\\\\Data_mining\\\\data_preprocess_practice.mat'#文件绝对路径
data = scipy.io.loadmat(datafile, mdict=None, appendmat=True) #载入MATLAB文件

scipy.io.loadmat ( file_name , mdict = None , appendmat = True , ** kwargs )

file_name:str型，mat 文件的名称（如果 appendmat==True，则不需要 .mat 扩展名）

mdict ：dict，可选，在其中插入 matfile 变量的字典

appendmat：bool，可选，True的话将.mat加到给定文件名末尾

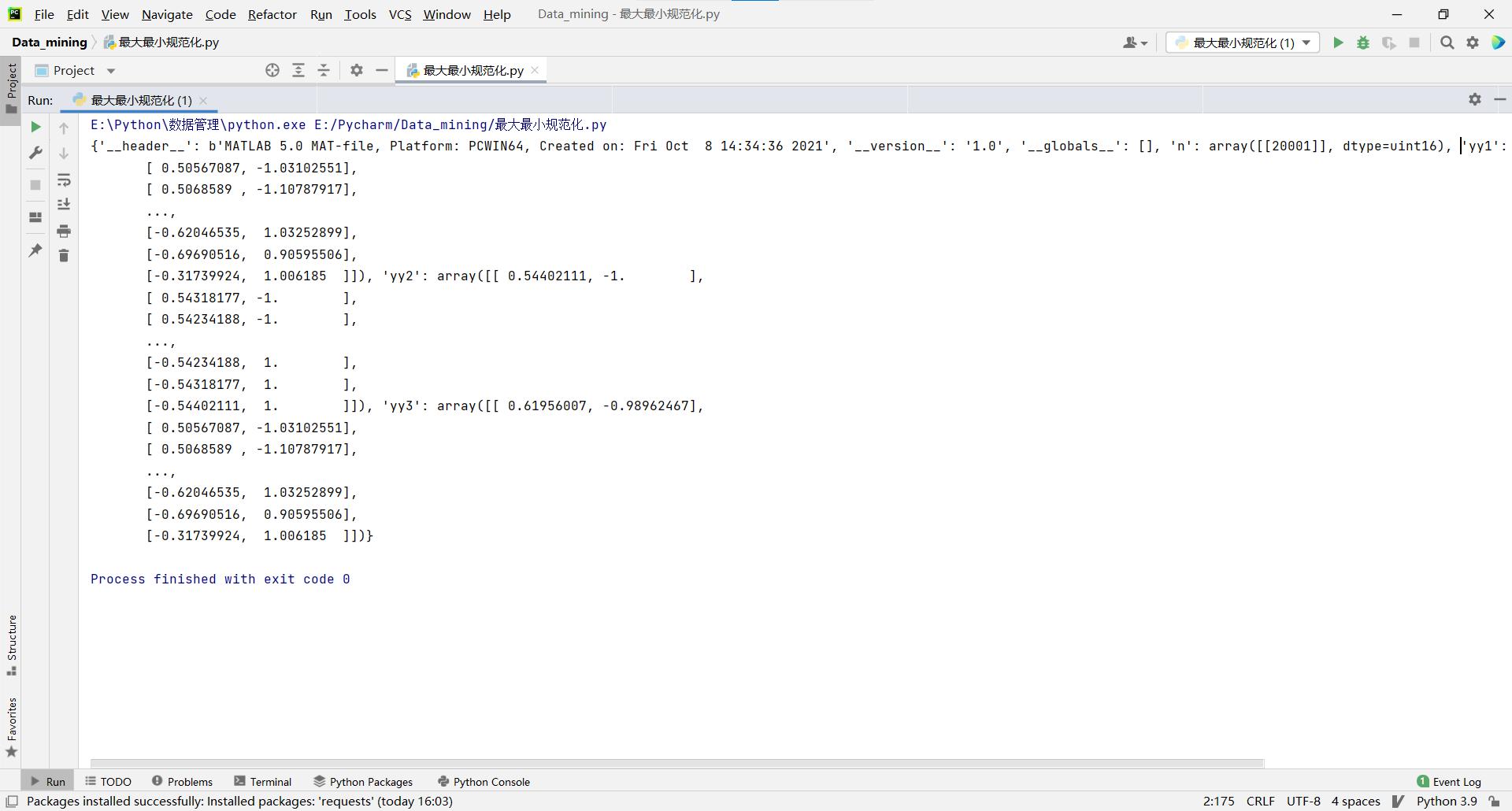
读取出来如图，这个数据由yy1、yy2、yy3等二维数组组成 

3.最大最小值规范化、零均值规范化代码实现

#取出yy1,yy2,yy3生成数组
yy1 = data['yy1']
yy2 = data['yy2']
yy3 = data['yy3']
#最大最小值规范化以及零均值规范化函数
def standard(y):
    #创建空数组存取第一、二列数
    tem_1 = []
    tem_2 = []
    #取出第一列和第二列数据
    for i in range(len(y)):    #此处也可用for i,item in enumerate(y):
        tem_1.append(y[i][0])
        tem_2.append(y[i][1])
    tem_1.sort()#对第一列数据进行排序
    tem_2.sort()
    max_1 = tem_1[-1]#取出第一列数据最大值
    min_1 = tem_1[0]#取出第一列数据最小值
    max_2 = tem_2[-1]
    min_2 = tem_2[0]
    xx = copy.deepcopy(y)#深拷贝以便后序进行零均值规范化
    # 最小-最大规范化：
    for j in range(len(y)):
        y[j][0] = (y[j][0] - min_1)/(max_1 - min_1)#公式为x' = (x - min)/(max - min)映射到[0,1]
        y[j][1] = (y[j][1] - min_2)/(max_2 - min_2)
    #零均值规范化
    tem_1_std = np.std(tem_1, ddof=1)  # 求第一列数据标准差
    tem_2_std = np.std(tem_2, ddof=1)
    tem_1_mean = np.mean(tem_1)  # 求第一列数据平均值
    tem_2_mean = np.mean(tem_2)
    for k in range(len(xx)):
        xx[k][0] = (xx[k][0] - tem_1_mean)/tem_1_std#公式为x' = (x - mean)/std
        xx[k][1] = (xx[k][1] - tem_2_mean)/tem_2_std
    print("最大最小规范化",y)
    plt.figure('第一列规范化分布')
    plt.plot(np.linspace(-40, 40, 20001), y[:, 0])
    plt.figure('第二列规范化分布')
    plt.plot(np.linspace(-40, 40, 20001), y[:, 1])
    print("零均值规范化",xx)
    #画出图像分布用于对比
    plt.figure('第一列零均值分布')
    plt.plot(np.linspace(-40, 40, 20001), xx[:, 0])
    plt.figure('第二列零均值分布')
    plt.plot(np.linspace(-40, 40, 20001), xx[:, 1])
    plt.show()
    return y,xx

 standa（yy1）运行结果如图：

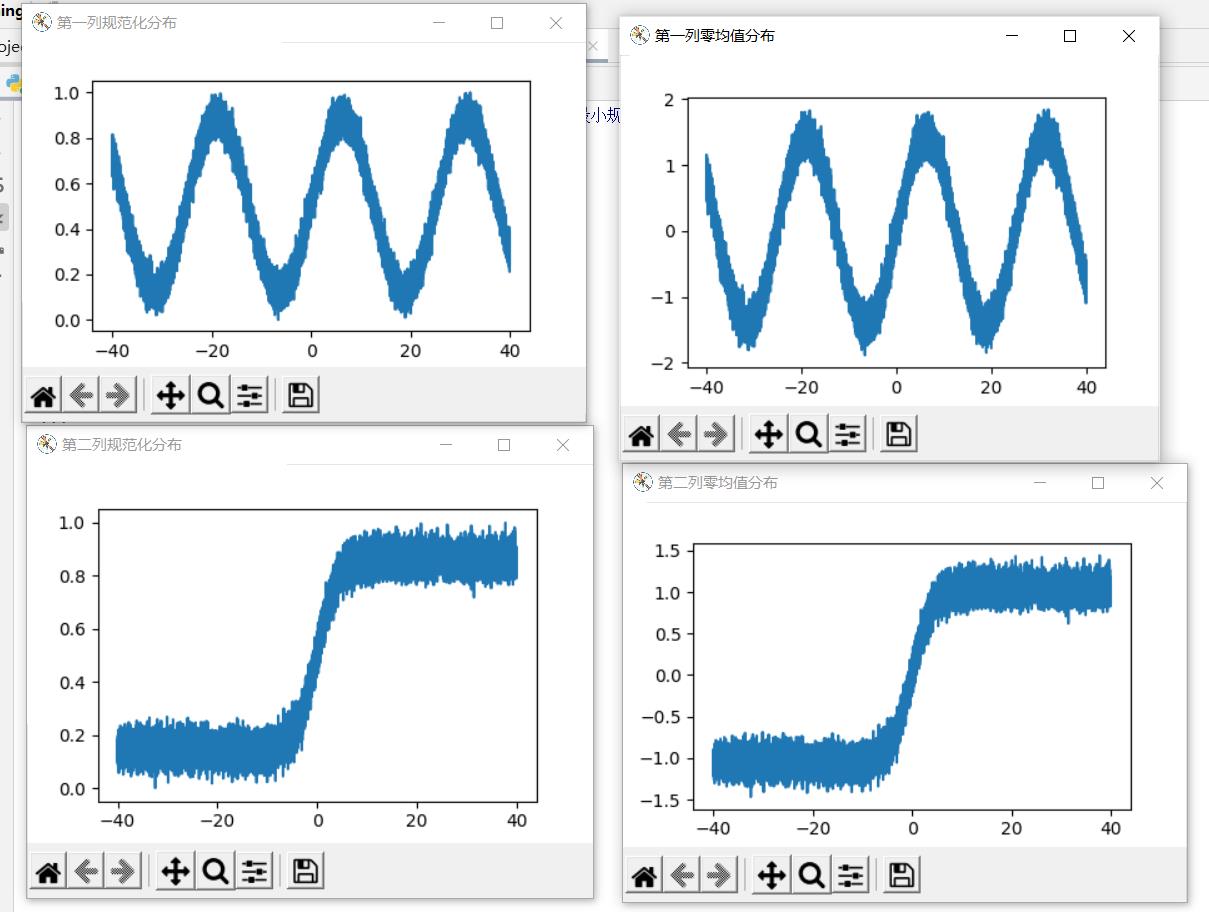
规范化后图形展示

 画出的图如图：

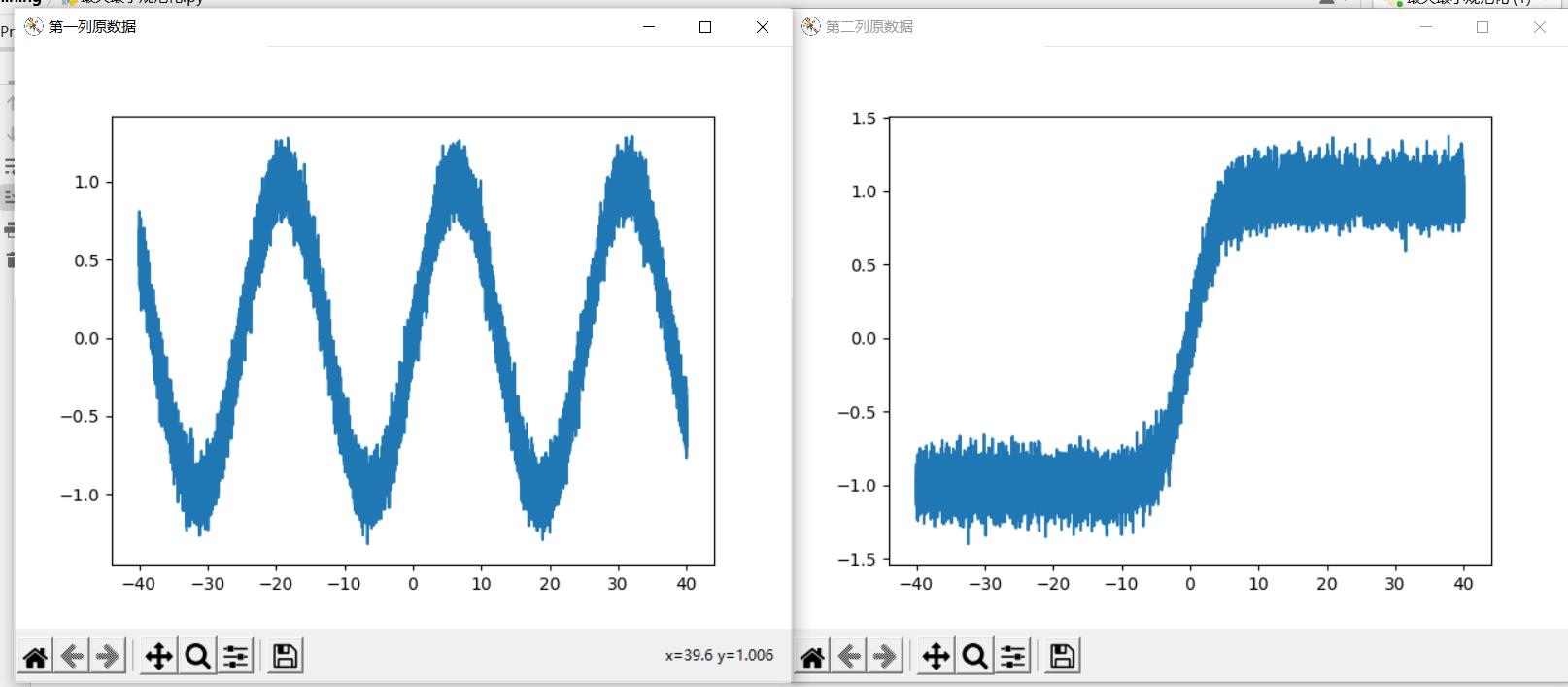
 与原始图像对比：

 代码中部分函数简介：

Array.sort(cmp=None, key=None, reverse=False)

cmp：用于比较的函数（大于时返回1，小于时返回-1，等于时返回0），比较什么由key决定,有默认值，迭代集合中的一项;
key：用列表元素的某个属性和函数进行作为关键字，有默认值，迭代集合中的一项;
reverse：排序规则. reverse = True 或者 reverse = False，有默认值。

copy.deepcopy()

将被复制对象完全再复制一遍作为独立的新个体单独存在。所以改变原有被复制对象不会对已经复制出来的新对象产生影响。

numpy.std(a, axis=None, dtype=None, out=None, ddof=0)  用于计算标准差

a： array_like，需计算标准差的数组
axis： int, 可选，默认情况是计算扁平数组的标准偏差。
dtype： dtype, 可选，用于计算标准差的类型。
out： ndarray, 可选，将结果放置在其中的替代输出数组。它必须具有与预期输出相同的形状，但如果有必要，类型(计算值的类型)将被转换。
ddof： int, 可选

 numpy.mean()用于计算平均值

plt.figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None, frameon=True)

num:图像编号或名称，数字为编号 ，字符串为名称

figsize:指定figure的宽和高，单位为英寸；

dpi:参数指定绘图对象的分辨率，即每英寸多少个像素

facecolor:背景颜色

edgecolor:边框颜色

frameon:是否显示边框

plt.plot(x,y,format_string,**kwargs) 
x:x轴数据

y:y轴数据

format_string:控制曲线的格式字串,其中包括颜色、风格、标记 

4.剔除奇异值和去除高斯噪声代码实现

注：此处代码承接上文·，是写在一个file中的

#剔除奇异值
def remove_singular(arr,n):
    #创建新数组用于存储原数据
    tem_1 = []
    tem_2 = []
    #取出第一列和第二列数据
    for i in range(len(arr)):
        tem_1.append(arr[i][0])
        tem_2.append(arr[i][1])
    tem_1_std = np.std(tem_1, ddof=1)  # 求第一列数据标准差
    tem_2_std = np.std(tem_2, ddof=1)
    tem_1_mean = np.mean(tem_1)  # 求第一列数据平均值
    tem_2_mean = np.mean(tem_2)
    #创建新数组用于存储剔除奇异值后的数据
    arr1 = []
    arr2 = []
    #提供一个阈值(此处取数组中数据的平均值+-2倍的标准差为阈值)削去奇异值
    for i in range(len(tem_1)):
        if tem_1[i] <= tem_1_mean + 2 * tem_1_std and tem_1[i] >= tem_1_mean - 2 * tem_1_std:
            arr1.append(tem_1[i])
    #展示原数据曲线图
    plt.figure('tem_1')
    plt.plot(np.linspace(-20,20,len(tem_1)),tem_1)#生成一个数量为len(tem_1)的等间距样本，在区间[-20,20]内
    #展示剔除奇异值后的曲线图像
    plt.figure('arr1')
    plt.plot(np.linspace(-20,20,len(arr1)),arr1)
    for j in range(len(tem_2)):
        if tem_2[j] <= tem_2_mean + 2 * tem_2_std and tem_2[j] >= tem_2_mean - 2 * tem_2_std:
            arr2.append(tem_2[j])
    plt.figure('tem_2')
    plt.plot(np.linspace(-20, 20, len(tem_2)), tem_2)
    plt.figure('arr2')
    plt.plot(np.linspace(-20,20,len(arr2)),arr2)
    #滑动平均去高斯噪声
    window = np.ones(n)/n
    c = np.convolve(arr1,window,'valid')#numpy中的卷积库函数，’valid‘返回的是完全重叠的点，边缘的点无效
    d = np.convolve(arr2,window,'valid')
    #展示去噪后的图线
    plt.figure('c')
    plt.plot(np.linspace(-20,20,len(c)),c)
    plt.figure('d')
    plt.plot(np.linspace(-20,20,len(d)),d)
    plt.show()
    return arr1,arr2,c,d

代码中部分函数简介：

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

start : 序列的起始点.

stop : 序列的结束点

num : 生成的样本数，默认是50。必须是非负。

endpoint : 如果True，'stop'是最后一个样本。否则，它不包括在内。默认为True。

numpy.convolve(a, v, mode='full')

a:第一个一维数组

v：第二个一维数组

mode：{‘full’:默认值，返回每个重叠点的卷积，输出形状为 (N+M-1,)；

              ‘valid’：返回长度为 max(M,N)-min(M,N)+1的输出；

              ‘same’：返回长度为max(M,N)的输出}

结果运行展示：

原数据：

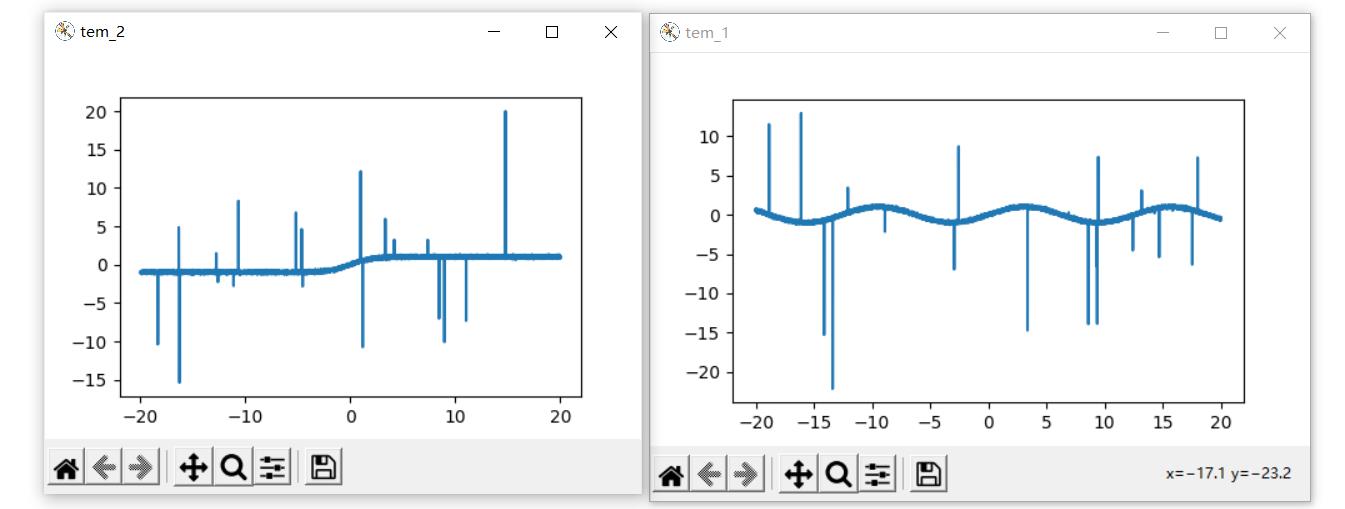
 剔除奇异值：

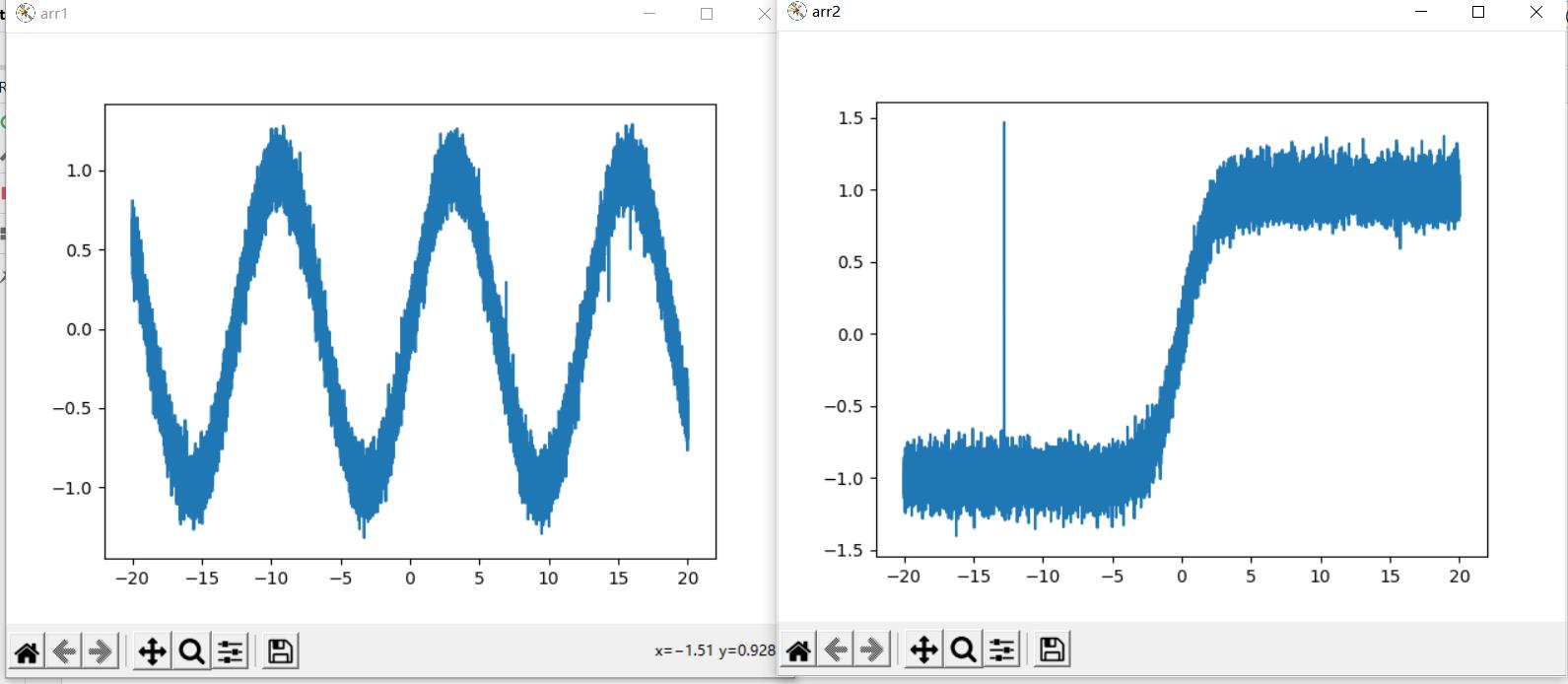
滑动平均去噪：

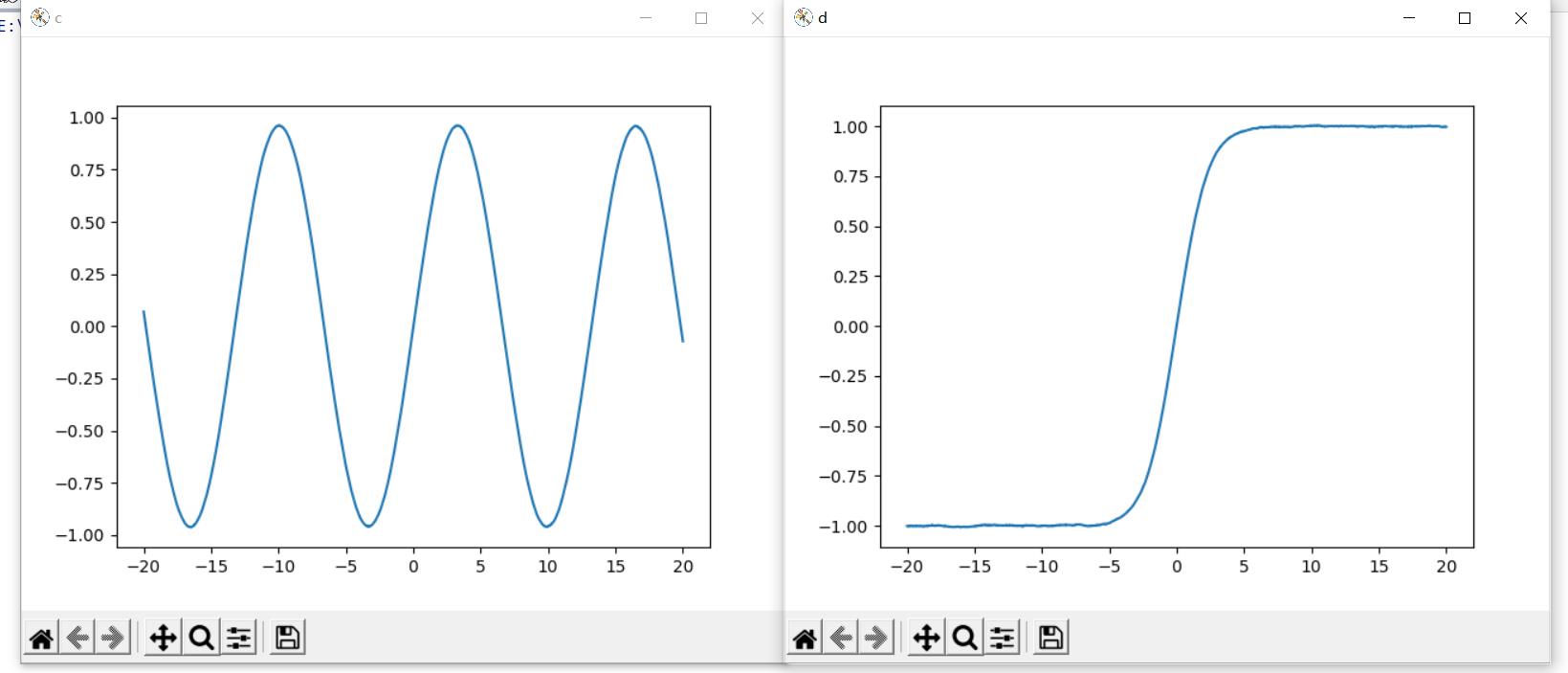
附加——拟合剔除奇异值、去噪后的曲线： 

    #拟合去噪后的每一列数据
    poly_c = np.polyfit(np.linspace(-20,20,len(c)),c,deg=9)#对第一列数据多项式（9阶）曲线拟合
    print("poly_c",np.poly1d(poly_c))#将拟合曲线函数表示出来
    poly_d = np.polyfit(np.linspace(-20, 20, len(d)), d, deg=20)  #对第二列数据多项式（20阶）曲线拟合
    print("poly_d",np.poly1d(poly_d))

numpy.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)

x:样本点的x坐标

y：样本点的y坐标。可以通过传入每列包含一个数据集的二维数组，同时拟合多个共享相同 x 坐标的样本点数据集。

deg：整数型，拟合多项式的次数

rcond：可选，拟合的相对条件。相对于最大奇异值而言小于此值的奇异值将被忽略

返回多项式系数，最高次幂优先

5.感谢申明

借鉴了numpy官网的使用指南，还有一些博主的文章，在此感谢！感谢！感谢！

也感谢各位看客，祝大家身体健康，学业有成，我们一起共同进步！