二叉树的定义和性质

Posted 2021-11-11 South.return

目录

二叉树的定义

二叉树的性质

性质1  在二叉树的第i层上至多有 2^(i-1)个结点。(i≥1)

性质2  深度为k的二叉树至多有2^(k)-1个结点。(k≥1)

性质3  对任何一棵二叉树T，若其终端结点数为n0，度数为2的结点数为n2，则n0=n2+1。

性质4  具有n个结点的完全二叉树的深度为[log n]+1 或 log (n+1)。

二叉树的定义

概述：所有结点的度都只为0、1、2的树，就是二叉树。 

定义：二叉树 (Binary Tree)是 n(n≥0)个结点的有限集合，它的每个结点至多只有两棵子树。它或者是空集，或者是由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。

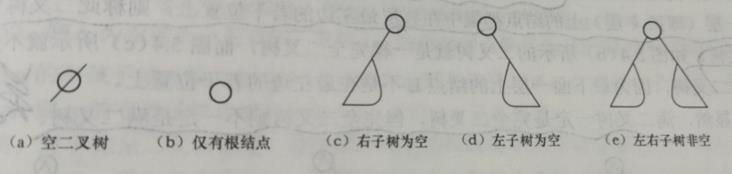
二叉树的五种基本形态：

二叉树的性质

性质1  在二叉树的第i层上至多有 2^(i-1)个结点。(i≥1)

证明：利用 ”数学归纳法" 进行证明。

(1) 当 i=1时，只有一个根结点，即 2^(i-1)=2^0=1。

(2) 归纳假设，第 i-1层上至多有 2^(i-2)个结点。因为二叉树的每个结点的度至多为 2，所以在 "第 i层上的结点数目” 最多是 “第 i-1层的结点数目的2倍”，即 2*2^(i-2)=2^(i-1)。

如图所示，当二叉树确定在哪一层时，有一个唯一对应的结点最大数的存在，这种对应关系可以看作是函数关系。

满足的关系式为：y=2^(i-1)（其中x为二叉树中的某一层，y为该层的最大结点数）

最后通过验证发现不管是在二叉树中的那一层，层数和对应的最大结点数都满足这个函数关系，所以该性质属于二叉树的特性。

性质2  深度为k的二叉树至多有2^(k)-1个结点。(k≥1)

证明：一颗深度为 k的二叉树最多含有的结点数，应该是该二叉树中每一层上最多含有结点数的总和。

当深度为 k时，二叉树的最大结点数为：2^0+2^1+2^2+…+2^(k-1) = 2^(k)-1。

性质3  对任何一棵二叉树T，若其终端结点数为n0，度数为2的结点数为n2，则n0=n2+1。

证明：设 n1为二叉树T中度为1的结点数，因为二叉树中所有结点的度都不大于 2，得出二叉树T结点总数为：n=n0+n1+n2。

度数为 1的结点表示它有一个孩子结点，度数为 2的结点有两个孩子结点，树中孩子结点的总数为：n1+2*n2。树中只有根节点不是任何结点的孩子结点，因此二叉树中的结点总数还可表示为：n=n1+2*n2+1。

根据两个总结点数公式可得：n0=n2+1。

性质4  具有n个结点的完全二叉树的深度为[log n]+1 或 log (n+1)。

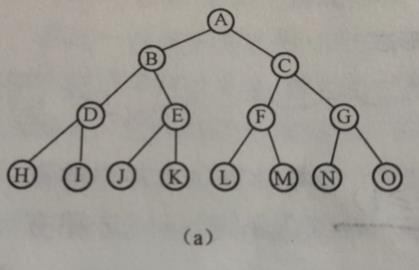
满二叉树：一棵深度为 k且有 2^(k)-1个结点的二叉树。图中的 a就是满二叉树。

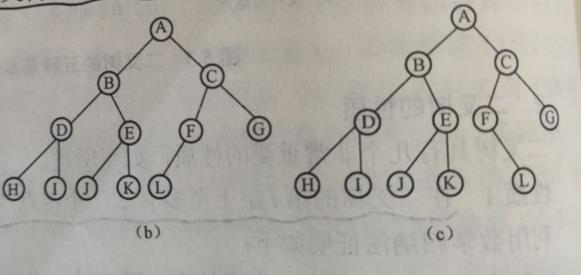
完全二叉树：一棵深度为 k的二叉树，其前 k-1层是一棵满二叉树，而最下面一层 (第k层)上的结点都集中在该层的最左边的若干位置上。

上图中的 b就是完全二叉树，c不是完全二叉树。

证明：假设二叉树的深度为 k，根据完全二叉树的定义，它的前 k-1层是深度为 k-1的满二叉树，共有 2^(k-1)-1个结点。因为二叉树的深度为 k，二叉树的结点数 n>2^(k-1)-1，由性质二可知 n≤2^(k)-1，所以有 2^(k-1)-1<n≤2^(k)-1。

 

由此可见，n个结点的完全二叉树的深度为 [log n]+1。

---