程序员的算法趣题Q58: 丢手绢游戏中的总移动距离
Posted 笨牛慢耕
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了程序员的算法趣题Q58: 丢手绢游戏中的总移动距离相关的知识,希望对你有一定的参考价值。
1. 问题描述


2. 解题分析
搜索最短距离,图搜索问题中的最短距离问题,可以用广度优先搜索策略来解决。
2.1 搜索树示意图
搜索树示意图如下:
2.2 算法流程
用一维数组表示当前状态,但是要注意实际上表达的是围成一圈的状态。

2.3 实现要点
- 0号玩家第一步固定地从把手绢丢在位置0(1号玩家)后面开始,因此BFS从1号玩家作为runner开始。0号玩家需要的步数不要忘记
- 搜索过程中不仅要记录当前状态,还需要记录到目前为止累积步数,当前runner,已经当前runner从哪个位置出发
- 计算当前runner丢手绢交换位置的步数时,需要注意runner需要先跑到预定位置,然后再跑一圈才能进入位置
- 考虑到围成一圈的对成性以及本题只要求相对位置变为逆序,因此在以上用一维数组来表示排列状态时,目标状态不是一个而是经过循环移位后等价的N个。参见代码中的isTargets()
3. 代码及测试
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 23 08:04:30 2021
@author: chenxy
"""
import sys
import time
import datetime
import math
# import random
from typing import List
from collections import deque
import itertools as it
import numpy as np
print(__doc__)
def isTargets(a, target):
for k in range(len(target)):
if np.array_equal(a, np.roll(target,k)):
return True
return False
N = 6
s0 = np.arange(1,N+1) # [1,2,3,...,N]
target = s0[::-1] # In fact, all the circular shift of it are targets
s1 = s0.copy()
s1[0] = 0 # [0,2,3,...,N]
q = deque()
visited = set()
q.append((tuple(s1),N,1,0)) # (states, step, runner, start)
visited.add(tuple(s0))
visited.add(tuple(s1))
# flog = open("Q58.log", "w")
# flog.write('state, steps, runner, start')
tStart = time.perf_counter()
isOK = False
while len(q) > 0:
cur,step,runner,start = q.popleft() #used as Queue instead of Stack in BFS.
# print(cur,step,runner,start)
# flog.write('{0}, {1}, {2}, {3},\\n'.format(cur,step,runner,start))
if isTargets(cur, target):
isOK = True
break
for k in range(N):
nxt = np.array(cur)
# interchange between runner and nxt[k]
nxt_runner = nxt[k]
nxt[k] = runner
if tuple(nxt) not in visited:
visited.add(tuple(nxt))
curSteps = ((k-start) if (k-start)>=0 else (k-start+N)) + N
q.append((tuple(nxt),step+curSteps,nxt_runner,k))
if not isOK:
print('Fails to reach the target states!')
# flog.close()
tCost = time.perf_counter() - tStart
print('N={0}, steps = {1}, tCost = {2:6.3f}(sec)'.format(N,step,tCost))运行结果:
N=6, steps = 48, tCost = 0.113(sec)
N=8, steps = 96, tCost = 21.311(sec)
4. 后记
运行时间太长了,需要进一步考虑优化。
N=8时的答案与原书答案是一致的,但是N=6时与原书给的题解要小(48 vs 51),经过仔细查验,确信原书给的答案不正确。原书给的移动过程所需要的步骤数的确更短,但是就总的移动距离而言我的更短。。。N=6时的我所得到的移动过程如下所示:
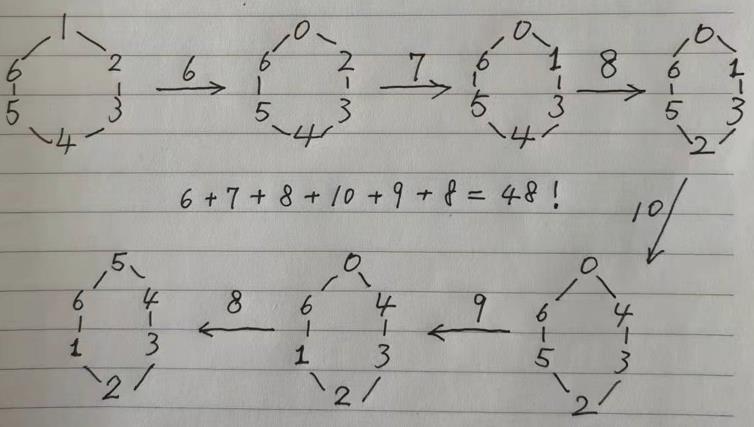
以上N=6的移动过程有兴趣的小伙伴可以检验。
心中有点小小的激动,找出一个“错误”不是一件容易的事情^-^。
上一篇:Q55: 平分蛋糕
下一篇:Q59: 合并单元格的方式
本系列总目录参见:程序员的算法趣题:详细分析和Python全解
以上是关于程序员的算法趣题Q58: 丢手绢游戏中的总移动距离的主要内容,如果未能解决你的问题,请参考以下文章