matlab遗传算法选址（多约束条件）

Posted 2021-11-10 张叔zhangshu

模型

配送网点包括：
自提柜——提供自提服务
联盟网点——提供送货上门或自提
在一个区域内有x个备选的用来提供两种服务的配送网点,已知备选共同配送网点的单日成本和可以提供的最大运营能力。有x个客户需求点,已知各个需求点的位置和需求量，并且每个需求点都存在【自提】和【送货上门】两种末端配送需求，
网点用s表示——数量x个
客户点用t表示——数量y个
L——网点类型，L={M,N},l=M,联盟网点 l=N自提柜
P——客户需求类型，P={m，n，o}p=m 送货上门 p=n 自提 p=o 既有送货又有自提
Csl——l类型网点S固定成本
qtp ——P类型客户点t的日均订单量
dl——L类型网点s的最小服务半径
Dl——L类型网点s的最大服务半径
dlst——L类型网点s到客户t的距离
λt——需要送货上门客户占比
1-λt——需要自提的客户占比
决策变量：
Xsl——0-1变量 表示是否选择l类型网点作为配送网点
Ystlp——0-1变量 表示l类型网点s是否为 p 类型客户提供服务

主程序展示

clear
clc
close all
tic
%% 用importdata这个函数来读取文件
% shuju=importdata('cc101.txt');
load('cc101');
shuju=c101;
% bl=importdata('103.txt');
bl=3;
cap=60;                                                        %车辆最大装载量
%% 提取数据信息

E=shuju(1,5);                                                    %配送中心时间窗开始时间
L=shuju(1,6);                                                    %配送中心时间窗结束时间
zuobiao=shuju(:,2:3);                                       %所有点的坐标x和y
pszx=zuobiao(1:4,:);
customer=zuobiao(5:end,:);                                       %顾客坐标
cusnum=size(customer,1);                                         %顾客数
v_num=20;                                                        %车辆最多使用数目
demands=shuju(5:end,4);                                          %需求量
a=shuju(5:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=shuju(5:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
s=shuju(5:end,7);                                                %客户点的服务时间
h=pdist(zuobiao);
dist=squareform(h);    
% dist=load('dist.mat');
% dist=struct2cell(dist);
% dist=cell2mat(dist);
dist=dist./1000;%距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
alpha=100000;                                                       %违反的容量约束的惩罚函数系数
belta=90;%违反时间窗约束的惩罚函数系数
belta2=60;
chesu=20;

NIND=300;                                                       %种群大小
MAXGEN=10;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum+v_num-1;                                %染色体长度=顾客数目+车辆最多使用数目-1
% N=cusnum;
%% 初始化种群
% init_vc=init(cusnum,a,demands,cap); 
dpszx = struct('ps',[], 'Chrom',[]);
dpszx.Chrom=InitPopCW(NIND,N,cusnum,a,demands,cap);     %构造初始解
ps=pszxxz(dpszx.Chrom,cusnum);
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')

 [VC,NV,TD,violate_num,violate_cus]=decode(dpszx.Chrom(1,:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
% [VC,NV]=cls(dpszx.Chrom(1,:),cusnum);
    
% [~,~,bsv]=violateTW(VC,a,b,s,L,dist,chesu,bl);
% disp(['总距离：',num2str(TD)]);
disp(['车辆使用数目：',num2str(NV),'，车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
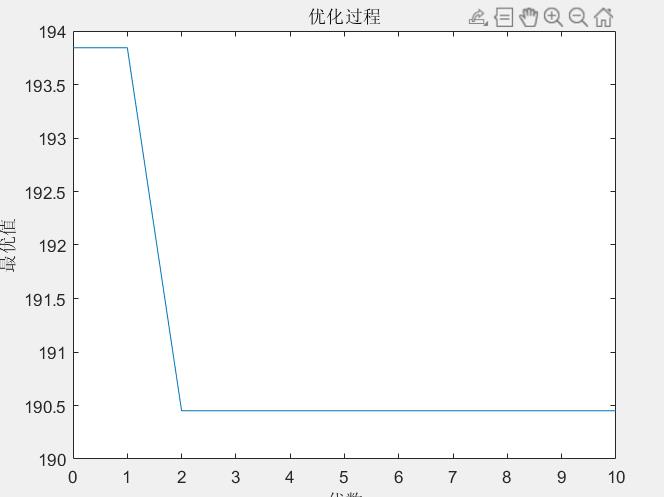
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
preObjV=min(ObjV);
%%
while gen<=MAXGEN
    %% 计算适应度
    ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
    line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)%画图 最优函数
    preObjV=min(ObjV);
    FitnV=Fitness(ObjV);
    %% 选择
    [SelCh,psc]=Select(dpszx.Chrom,FitnV,GGAP,ps);
    %% OX交叉操作
    [SelCh,psc]=Recombin(SelCh,Pc,psc,cusnum);
    %% 变异
    [SelCh,psc]=Mutate(SelCh,Pm,psc,cusnum);
    %% 重插入子代的新种群
    [dpszx.Chrom,ps]=Reins(dpszx.Chrom,SelCh,ObjV,psc,ps);
    %% 打印当前最优解
    ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(dpszx.Chrom(minInd(1),:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\\n')
    %% 更新迭代次数
    gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp('最优解:')
bestChrom=dpszx.Chrom(minInd(1),:);
bestps=ps(minInd(1),:);
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestChrom,cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
disp('-------------------------------------------------------------')
% [cost]=costFuction(bestVC,a,b,s,L,dist,demands,cap,alpha,belta,belta2,chesu,bl,);
%% 画出最终路线图
draw_Best(bestVC,zuobiao,bestps);
% save c101.mat
% toc

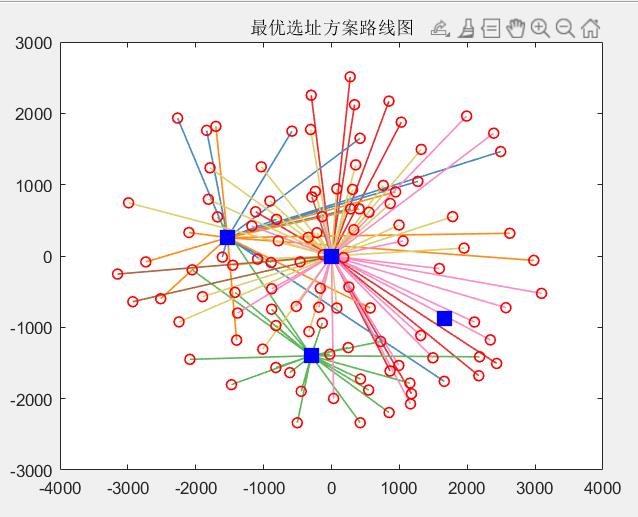
选址点1：1->29->28->27->26->25->24->23->22->21->20->1
选址点2：4->33->43->41->40->39->38->37->36->35->34->32->4
选址点3：2->48->62->60->58->56->55->54->53->52->51->50->49->47->76->75->74->73->72->71->70->69->2
选址点4：4->78->90->85->84->83->82->81->80->79->77->4
选址点5：1->92->100->105->108->107->106->104->103->101->2->14->13->12->59->99->86->57->97->96->95->93->9->8->7->5->4->3->1->91->89->88->87->1
选址点6：1->16->11->10->94->1
选址点7：1->19->18->17->15->31->30->46->98->102->6->65->64->63->61->67->68->66->45->44->42->1

最开始的点为选择的配送中心（代码中一共四个备选中心）

如需帮助
VX：zhangshu2274