第4章 组合逻辑电路
Posted 可能自洽
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第4章 组合逻辑电路相关的知识,希望对你有一定的参考价值。
第4章 组合逻辑电路
一、概述
1.组合逻辑电路定义
数字电路分类:
-组合逻辑电路
-时序逻辑电路
组合逻辑电路概念:任意时刻的输出仅取决于当时的输入信号,而与电路原来的状态无关。
组合逻辑电路特点:
结构上:只由逻辑门电路组成,没有记忆单元
功能上:只有从输入到输出的通路,没有从输出反馈到输入的回路
二、组合逻辑电路的分析方法
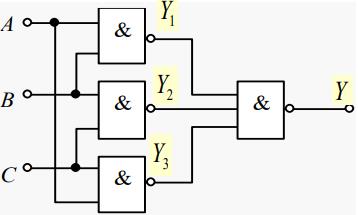
例 3人表决电路
Y
1
=
(
A
B
)
′
Y_1=(AB)'
Y1=(AB)′
Y
2
=
(
B
C
)
′
Y_2=(BC)'
Y2=(BC)′
Y
3
=
(
A
C
)
′
Y_3=(AC)'
Y3=(AC)′
Y
=
(
Y
1
Y
2
Y
3
)
′
=
(
(
A
B
)
′
(
B
C
)
′
(
A
C
)
′
)
′
=
A
B
+
B
C
+
A
C
Y=(Y_{1} Y_{2} Y_{3})'=((AB)'(BC)'(AC)')'=AB+BC+AC
Y=(Y1Y2Y3)′=((AB)′(BC)′(AC)′)′=AB+BC+AC

是一个3人表决电路:2人以上同意,表决就通过
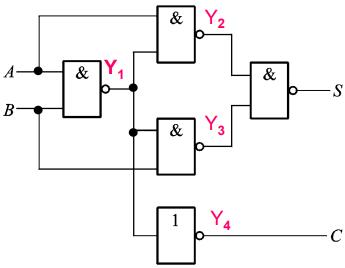
例 两个一位二进制数相加电路
Y
1
=
(
A
B
)
′
Y_{1}=(A B)^{\\prime}
Y1=(AB)′
Y
2
=
(
A
Y
1
)
′
=
(
A
(
A
B
)
′
)
′
=
A
′
+
A
B
=
A
′
+
B
Y_{2}=\\left(A Y_{1}\\right)^{\\prime} =\\left(A(A B)^{\\prime}\\right)^{\\prime}=A^{\\prime}+AB=A^{\\prime}+B
Y2=(AY1)′=(A(AB)′)′=A′+AB=A′+B
Y
3
=
(
Y
1
B
)
′
=
(
(
A
B
)
′
B
)
′
=
A
B
+
B
′
=
A
+
B
′
Y_{3}=(Y_{1} B)^{\\prime} =((A B)^{\\prime} B)^{\\prime} =AB+B^{\\prime}=A+B^{\\prime}
Y3=(Y1B)′=((AB)′B)′=AB+B′=A+B′
Y
4
=
Y
1
′
=
A
B
Y_{4}=Y_{1}^{\\prime}=A B
Y4=Y1′=AB
S
=
(
Y
2
Y
3
)
′
=
Y
2
′
+
Y
3
′
=
(
A
′
+
B
)
′
+
(
A
+
B
′
)
′
=
A
B
′
+
A
′
B
=
A
⊕
B
S=(Y_{2} Y_{3})^{\\prime}=Y_{2}^{\\prime}+Y_{3}^{\\prime}=(A^{\\prime}+B)^{\\prime}+(A+B^{\\prime})^{\\prime} =A B^{\\prime}+A^{\\prime} B=A \\oplus B
S=(Y2Y3)′=Y2′+Y3′=(A′+B)′+(A+B′)′=AB′+A′B=A⊕B
C
=
Y
4
=
A
B
C=Y_{4}=A B
C=Y4=AB
A
B
S
C
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
\\begin{array}{|c|c|c|c|} \\hline \\mathrm{A} & \\mathrm{B} & \\mathrm{S} & \\mathrm{C} \\\\ \\hline 0 & 0 & 0 & 0 \\\\ \\hline 0 & 1 & 1 & 0 \\\\ \\hline 1 & 0 & 1 & 0 \\\\ \\hline 1 & 1 & 0 & 1 \\\\ \\hline \\end{array}
A0011B0101S0110C0001
该电路实现两个一位二进制数相加的功能。S是它们的和,C是向高位的进位。由于这一加法器电路没有考虑低位的进位,所以称该电路为半加器
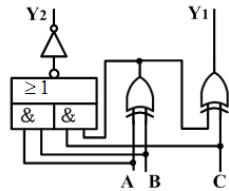
例 全加器
Y
1
=
A
⊕
B
⊕
C
Y_{1}=A \\oplus B \\oplus C
Y1=A⊕B⊕C
Y
2
=
A
B
+
(
A
⊕
B
)
C
Y_{2}=A B+(A \\oplus B) C
Y2=AB+(A⊕B)C

由真值表可知,该电路为全加器。A和B为两个加数,C是来自低位的进位,Y1是和,Y2是向高位的进位
三、组合逻辑电路的基本设计方法
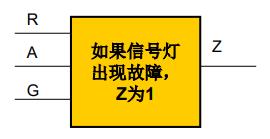
例 设计一个监视交通信号灯状态的逻辑电路
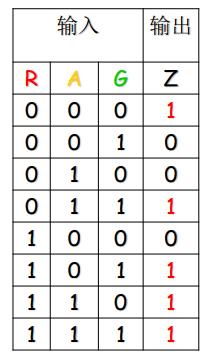
Z
=
R
′
A
′
G
′
+
R
′
A
G
+
R
A
′
G
+
R
A
G
′
+
R
A
G
Z=R^{\\prime}A^{\\prime}G^{\\prime}+R^{\\prime}AG+RA^{\\prime}G+RAG^{\\prime}+RAG
Z=R′A′G′+R以上是关于第4章 组合逻辑电路的主要内容,如果未能解决你的问题,请参考以下文章