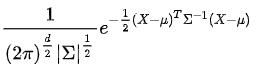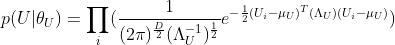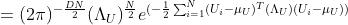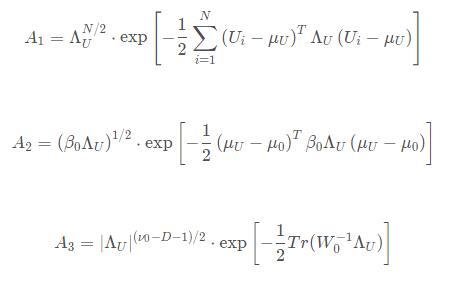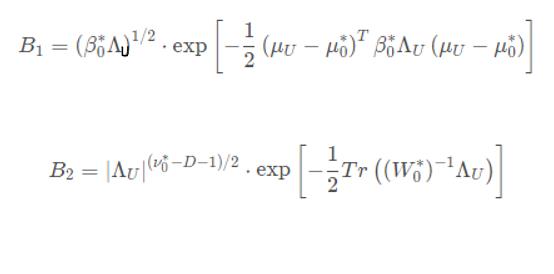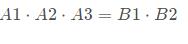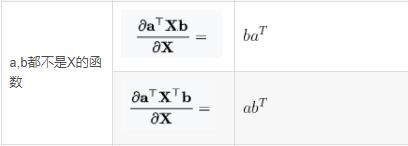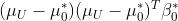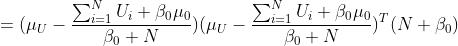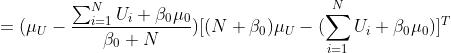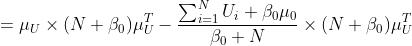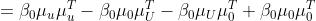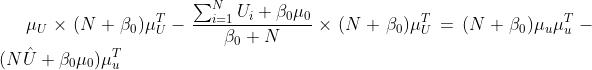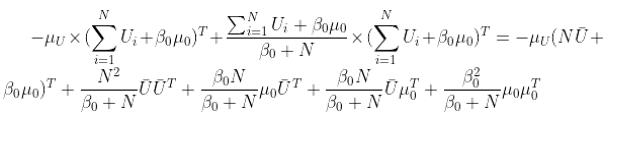BPMF论文辅助笔记： 固定U，更新θU 部分推导

Posted 2021-11-09 UQI-LIUWJ

该部分是辅助论文笔记 Bayesian Probabilistic Matrix Factorizationusing Markov Chain Monte Carlo （ICML 2008）_UQI-LIUWJ的博客-CSDN博客 的3.3.1小节

1 多元高斯分布&威沙特分布

 复习一下多元高斯分布的概率密度函数：

复习一下威沙特分布的概率密度函数

 概率统计笔记：威沙特分布（Wishart Distribution）_UQI-LIUWJ的博客-CSDN博客

 2  推导

 固定U，采样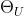，按照概率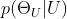进行采样

利用条件概率性质，我们可以用已知的条件概率来计算: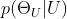

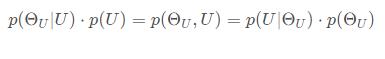
 由于此时U已知，故p(U)为常量

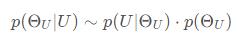
 右侧第一项是一个高斯分布，第二项是高斯分布和威沙特分布的乘积。

2.1  第一项的展开

 先看第一项：

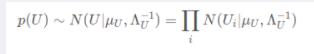
所以 可以看成是N个高斯分布的乘积

                   

2.2 第二项的展开 

 再看第二项

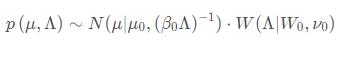
 我们拆成高斯分布的概率密度和威沙特分布的概率密度：

 2.2.1 高斯分布

高斯分布的概率密度：

                                        

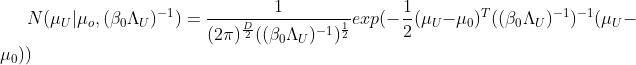
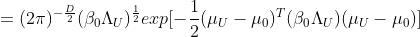
2.2.2 威沙特分布 

 威沙特分布的概率密度：

 

 

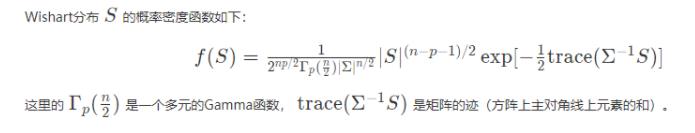
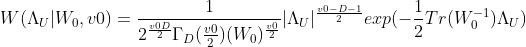
 2.3 合并

 去掉不需要的系数项，我们有：

 

 我们希望通过采样得到的 （）也满足高斯威沙特分布：

 也就是我们也就是我们希望找到一组B1，B2

 使得

2.4 求值

2.4.1 v0*

 我们考虑等号两边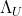的指数：

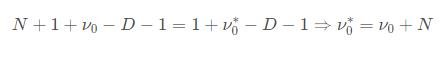
2.4.2 β0*

  我们考虑指数中的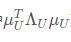项的系数 ：

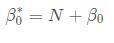
2.4.3 μ0*

•  我们考虑指数中的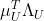项的系数

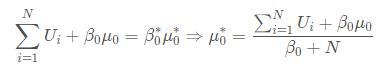
2.4.4 W*

 至于W*，就比较繁琐

 至于W*，就比较繁琐

我们先回顾两个求导的知识

 线性代数笔记：标量、向量、矩阵求导_UQI-LIUWJ的博客-CSDN博客

 

  于是我们对(A1+A2+A3)和(B1+B2)的指数项关于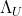求导

先看A这边的

A1指数项求完导是（由于都有-1/2，所以我都约去）：

  A2指数项求完导是

A2指数项求完导是 

 再看B这边的：

 B1指数项求完导是：

B2指数项求完导是

 于是我们有：

+

=++(1)

 而在前面我们已经得到：

 

 

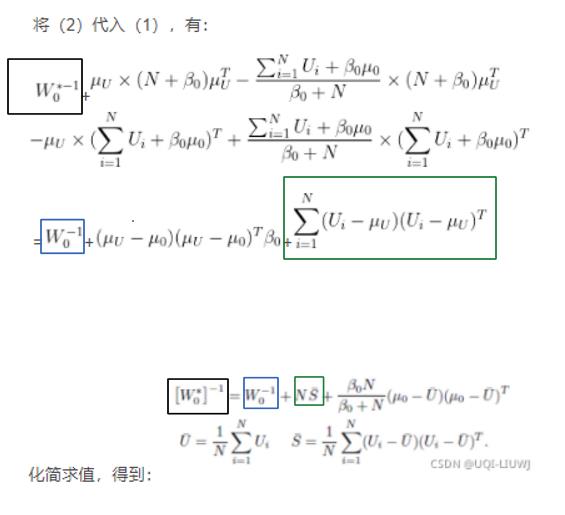
 代入进去，有：

 

 

 (2)

 

 

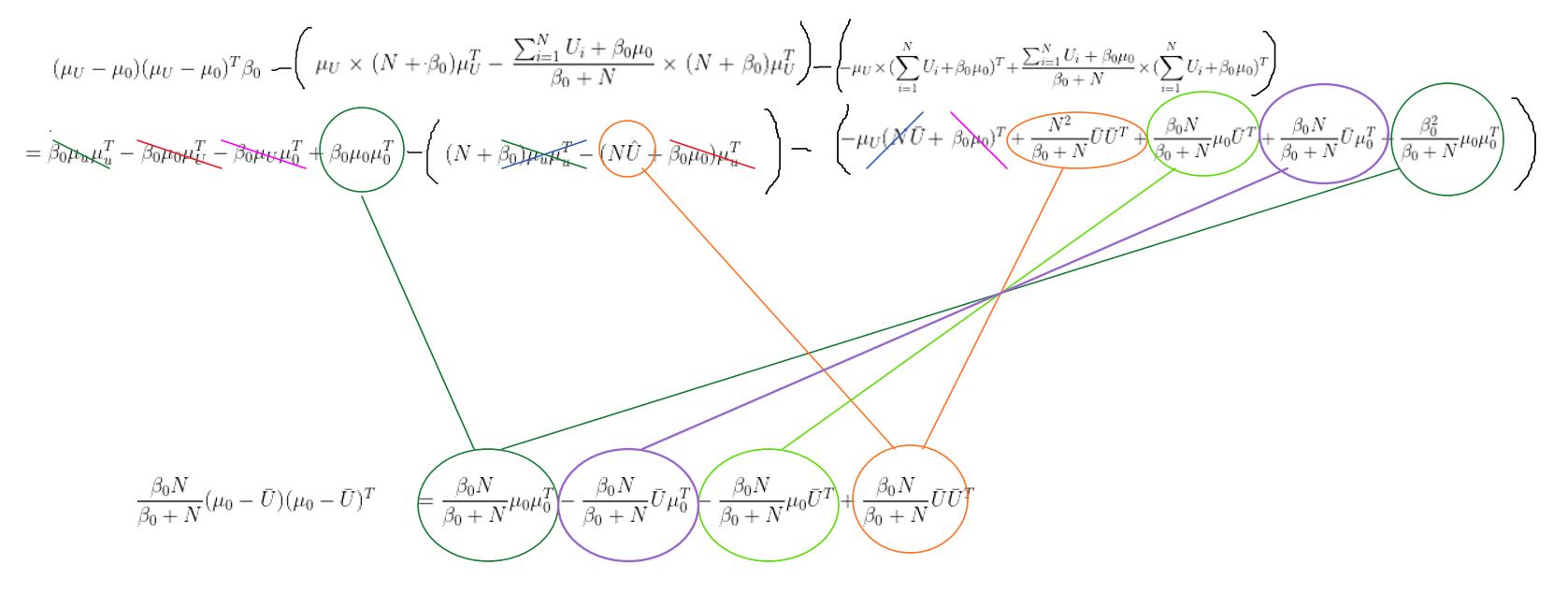
  现在就是剩下的部分怎么算了：

 展开消元即可