最强解析面试题：矩形覆盖「建议收藏！」

Posted 2021-11-09 魏小言

文章目录

• 最强解析面试题：矩形覆盖「建议收藏！」
• • • 题目
    • • 示例1
      • 示例2
    • 思路
    • 代码
  • Q&A
  • 附录

最强解析面试题：矩形覆盖「建议收藏！」

文章讲解 “ 矩形覆盖 ” 经典面试题，包含思路及源码，及解惑！

题目

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，从同一个方向看总共有多少种不同的方法？

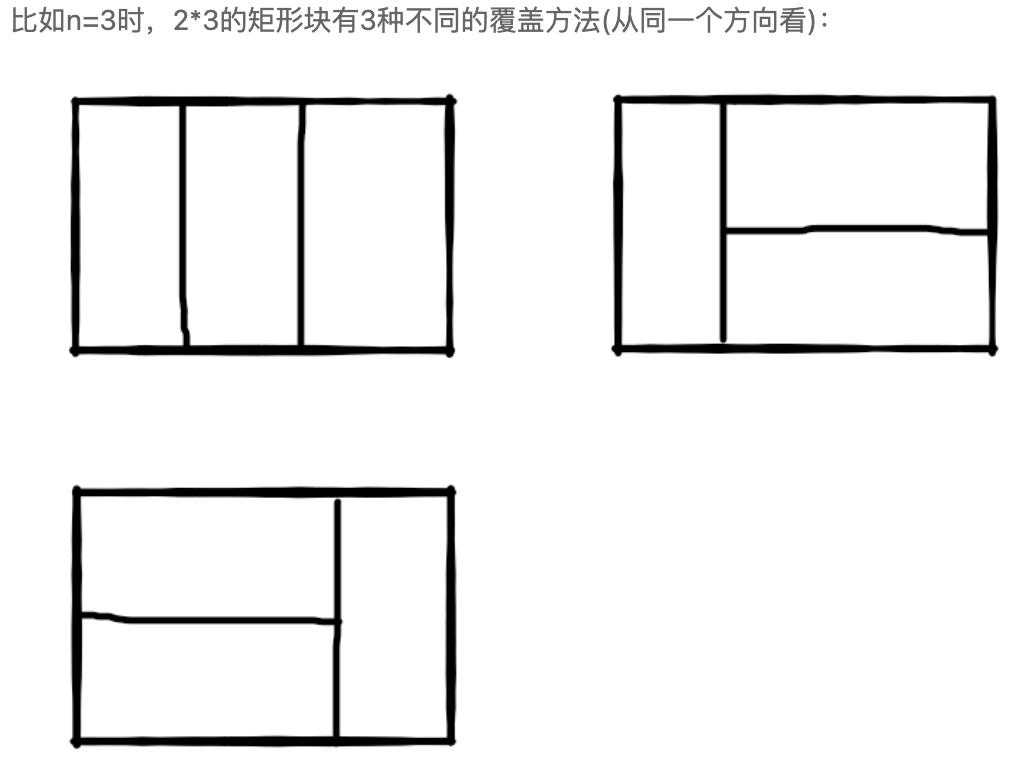
示例1

输入：
0
返回值：
0

示例2

输入：
4
返回值：
5

思路

以 f(n) 为 n 个 2*1 小矩形覆盖方法数，则在覆盖过程中，末尾的方法有两种：

• 一个 2*1 小矩形竖直摆放，此时方法总数是 f(n-1)
• 两个 2*1 小矩形水平摆放，此时方法总数是 f(n-2)
  故，综合 n 个大矩形总的概率为 f(n-1) + f(n-2) ，即 f(n) = f(n-1) + f(n-2)。

注意：n == 0 , f(n) = 0；n == 1，f(n) = 1。

代码

package main

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 * 
 * @param number int整型 
 * @return int整型
*/
func rectCover( number int ) int {
    // write code here
     if number == 0{
        return 0
    }
    if number == 1{
        return 1
    }
    if number == 2{
        return 2
    }
  
    return rectCover(number-1)+rectCover(number-2)
}

Q&A

1、相同的还有 “ 斐波那契数列 “、“ 矩形覆盖 “ 题目

见前后篇博文

附录

递归结构注意入口、出口、处理逻辑即可。