2021-10-17
Posted 越登高望远
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021-10-17相关的知识,希望对你有一定的参考价值。
一、原理介绍
1.1 简介
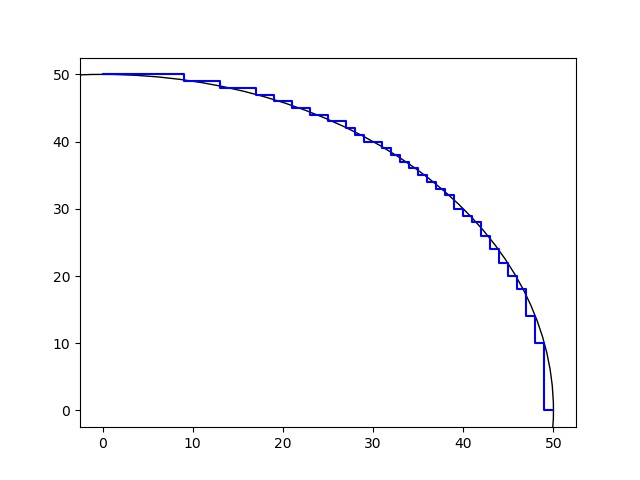
本文章灵感来源于机床数控技术及应用课程,上课老师提过,机床在加工一条直线或者圆弧的时候其实并不是按照理想的轨迹去加工的,其运动轨迹放大之后是锯齿状的(如下图所示),是通过逼近理想轨迹来加工的。那如何通过给定直线两个点,或者圆弧的起点终点,就能找到其运动轨迹呢?因为前阵子刚接触一个四轴电装机器臂,对其运动轨迹也比较感兴趣,可能跟课本的数控加工算法不一样,所以就打算练练手,将算法实现一下。
1.2 逐点比较法偏差计算(直线)
1.2.1 第一象限逐点比较法思路
如何去评价在直线的上方?本文以斜率绝对值来进行比较。

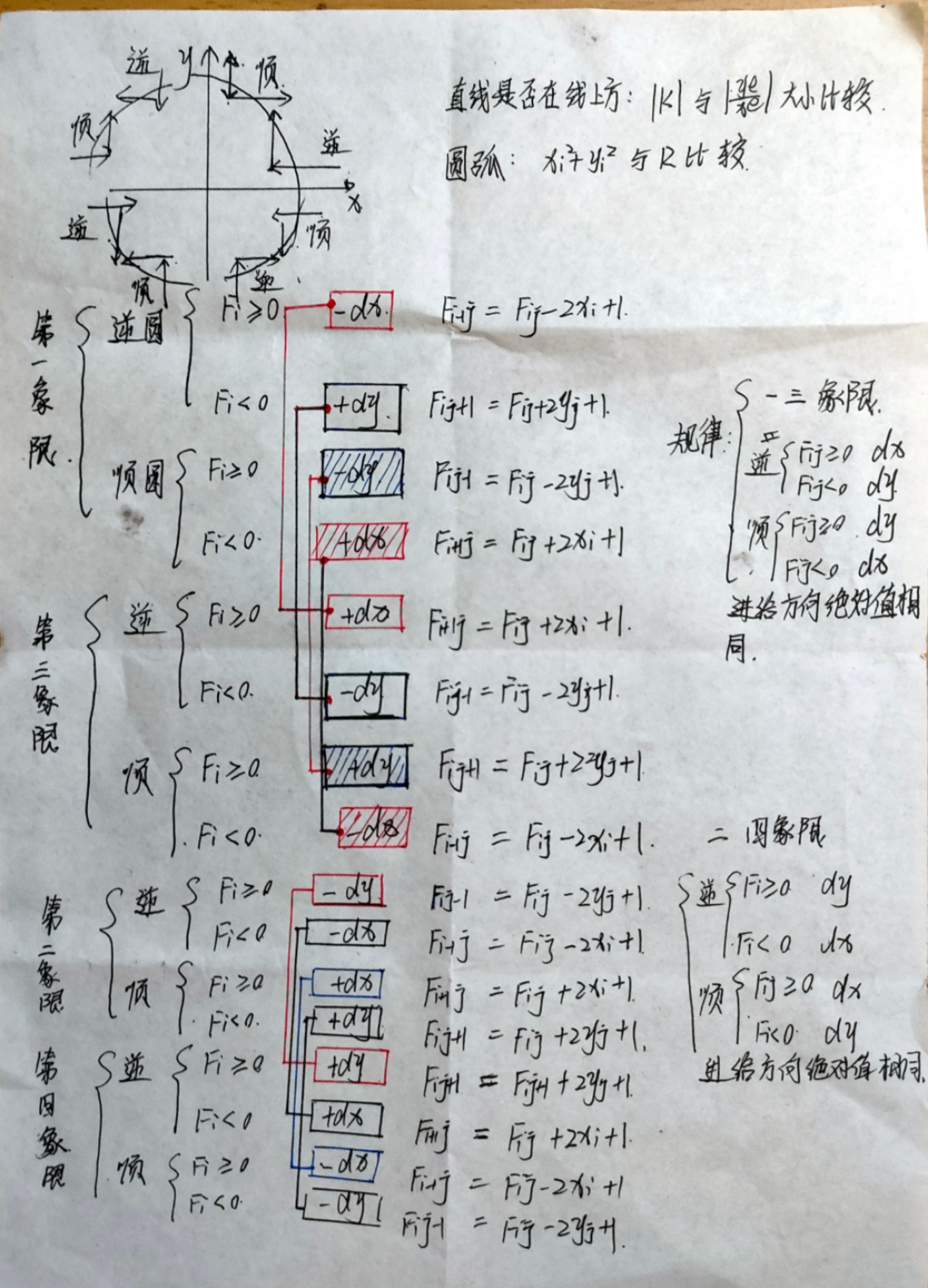
1.2.2 四象限逐点比较法实现思路
- 效率较低的方法是,分别写出四个象限情况的程序,根据输入去判断然后进入对应的程序计算就行。这种情况也能够实现,但是不太建议。遇到问题,我们是先进行分析,根据四象限直线的特征,以及上面提到的根据直线斜率来判断点在直线上方或者直线下方。
- 以这个指标来比较,不难发现在直线上方的所有点进给方向都是x轴方向,直线下方的进给方向都是y轴方向。 还有一个规律就是,终点在哪一象限,x或y的符号是什么,就往正方向或者负方向进给。
- 可能大家也有一个疑问,就是起点不在原点怎么办?很简单,大家只需要利用终点坐标—起点坐标,这样就是以起点坐标为(0,0),终点坐标对于起点来说就是相对坐标。这跟数控机床编程时,可以用到相对坐标增量来计算类似。

1.3 逐点比较法偏差计算(圆弧)
1.3.1 第一象限逐点比较法思路(圆弧)
大家可以参考下图第一象限的逆时针以及顺时针讲解。
1.3.2 四象限逐点比较法实现思路(圆弧)
1.相对于直线插补算法,四象限的圆弧插补确实不好理解,不过也不难,只要大家根据下面的规律总结以及课本,根据规律多尝试就能编出程序。
2.四象限的圆弧插补主要难在顺逆选方向的判断,以及如何确定进给方向?如何确定第几象限?其实只要这三个问题解决了,问题就迎刃而解。
3.顺逆时针的判断:利用法向量进行判断,这个是属于高数的内容,大家可以回去翻一下书,这里我是直接CSDN。旋转判断参考链接
4.象限判断:如何进行象限判断,考虑到圆弧起点以及终点都在坐标轴上,那么如何去判断呢?因此我采用了,((Xs+Xe)/3,(Ys+Ye)/3) 作为判断点。可以判断圆弧起点所在象限。因为无论中终点是否跨象限,都是进行运行计算。
备注:(Xs,Ys):起点坐标,(Xe,Ye):终点坐标。

二、程序实现思路
2.1 直线插补
1.先对起点在原点,第一象限直线进行插补
2.起点不在原点的直线,通过求终点相对于起点的相对坐标,这样起点就是原点。
3.根据 (Xi,Yi)与原点(起点)所车成直线斜率跟终点与原点(起点)斜率之间的关系,判断进给是x或者y方向。再根据起点坐标所在象限,得出x,y的正负,再根据正负求其进给方向。
2.2 圆弧插补
1.同时是先简单后再到难,第一步我们先根据第一象限圆弧,顺逆旋转的特点(看纸质版图解+课本+网上资料会更好理解)。
2.第二步就有些绕,需要根据四象限,顺逆时针旋转,进给方向是往正负x或者正负y。是不是有点乱。不着急,其实大家只要将全部进给方向都以第一象限的逆时针作为参考,通过上图变换规律作为理解。先以第一象限设定好进给x,y,再根据象限判断、旋转方向判断,确定实际进给方向,然后根据进给方向符号,直接求偏差。问题就迎刃而解。(建议大家看代码理解会更好)
三、代码展示
3.1直线插补程序以及效果
3.1.1 第一象限直线插补程序
# 作者:仲恺农业工程学院 冯耿鑫
# 日期:2021/10/12
# 功能:逐点比较法实现:第一象限过原点
# 参考链接:https://blog.csdn.net/joogle/article/details/7962320
# 输入直线终点坐标
import matplotlib.pyplot as plt # 画图库
from matplotlib.pyplot import MultipleLocator # 坐标设定库
end_pos = input("请输入直线终点坐标:\\t")
end_pos = end_pos.split(',')
Xe = int(end_pos[0])
Ye = int(end_pos[len(end_pos)-1])
n = Xe + Ye
Fi= [0] # 判别偏差
x = [0] # 每个x坐标
y = [0] # 每个y坐标
pos = [(0,0)] # 每个点的坐标
print("判别\\t\\t\\t进给\\t\\t\\t运算\\t\\t\\t比较\\t\\t\\t")
for i in range(n):
# 正偏差,位于直线上方
if Fi[i] >=0 :
dir = "+dx" # 往x正方向
print(Fi[-1],end="\\t\\t\\t")
F_temp = Fi[-1] - Ye # 迭代发偏差运算
x_temp = x[i]+1 # 记录下一个x坐标,x[i+1] = x[i]
y_temp = y[i] # 记录下一个y坐标,y[i+1] = y[i]
x.append(x_temp) # 对每一个x坐标进行储存
y.append(y_temp) # 对每一个y坐标进行储存
pos_temp = (x_temp,y_temp) # 对每一个坐标点进行储存
pos.append(pos_temp)
Fi.append(F_temp) # 对运算偏差进行存储
print(dir,end="\\t\\t\\t")
print(Fi[-1],end="\\t\\t\\t")
print(n-i)
else:
dir = "+dy" # 往y正方向
print(Fi[-1],end="\\t\\t\\t")
print(dir,end="\\t\\t\\t")
F_temp =Fi[-1] + Xe # 迭代发偏差运算
y_temp = y[i]+1 # 记录下一个y坐标,y[i+1] = y[i]+1
x_temp = x[i] # 记录下一个x坐标,其中x不变x[i+1] = x[i]
x.append(x_temp) # 对每一个x坐标进行储存
y.append(y_temp) # 对每一个y坐标进行储存
pos_temp =(x_temp,y_temp) # 对每一个坐标点进行储存
pos.append(pos_temp)
Fi.append(F_temp) # 对运算偏差进行存储
print(Fi[-1],end="\\t\\t\\t")
print(n-i)
# 画图
plt.plot([0,Xe],[0,Ye],color = 'r')
plt.plot(x,y,'o',color='b')
plt.plot(x,y)
plt.title('line',fontsize=24)
plt.tick_params(axis='both',which='major',labelsize=14)
plt.xlabel('x',fontsize=14)
plt.ylabel('y',fontsize=14)
x_major_locator=MultipleLocator(1)
#把x轴的刻度间隔设置为1,并存在变量里
y_major_locator=MultipleLocator(1)
#把y轴的刻度间隔设置为10,并存在变量里
ax=plt.gca()
#ax为两条坐标轴的实例
ax.xaxis.set_major_locator(x_major_locator)
#把x轴的主刻度设置为1的倍数
ax.yaxis.set_major_locator(y_major_locator)
#把y轴的主刻度设置为10的倍数
plt.xlim(-0.5,Xe+1)
#把x轴的刻度范围设置为-0.5到11,因为0.5不满一个刻度间隔,所以数字不会显示出来,但是能看到一点空白
plt.ylim(-0.5,Ye+1)
#把y轴的刻度范围设置为-5到110,同理,-5不会标出来,但是能看到一点空白
plt.savefig('.\\\\1.jpg')
plt.show()
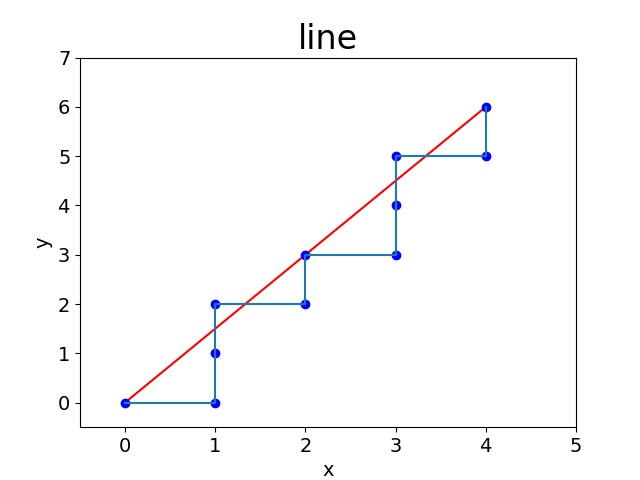
3.1.2 第一象限直线插补程序运行效果
请输入直线终点坐标: 4,6
判别 进给 运算 比较
0 +dx -6 10
-6 +dy -2 9
-2 +dy 2 8
2 +dx -4 7
-4 +dy 0 6
0 +dx -6 5
-6 +dy -2 4
-2 +dy 2 3
2 +dx -4 2
-4 +dy 0 1
3.1.3 四象限直线插补代码
# 作者:冯耿鑫
# 日期:2021/10/12
# 功能:逐点比较法实现:第一象限过原点
# 参考链接:https://blog.csdn.net/joogle/article/details/7962320
# 输入直线终点坐标
# 有input的时候,要调试就需要用到这个
# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt # 画图库
from matplotlib.pyplot import MultipleLocator # 用来调整坐标轴
start_pos = input("请输入直线起点坐标:\\t") # 获取起点坐标
end_pos = input("请输入直线终点坐标:\\t") # 获取终点坐标
start_pos = start_pos.split(',') # 对','进行拆分
end_pos = end_pos.split(',')
Xs = int(start_pos[0]) # 起点x
Ys = int(start_pos[len(start_pos)-1]) # 起点y
Xe = int(end_pos[0]) # 终点x
Ye = int(end_pos[len(end_pos)-1]) # 终点y
Xe = Xe - Xs # 终点相对坐标x
Ye = Ye - Ys # 终点相对坐标y
n = abs(Xe) + abs(Ye) # 步数
x = [0] # 起点x
y = [0] # 起点y
pos = [(0,0)] # 每个点的坐标,初始化起点坐标为(0,0)
# 用于判断进给方向,例如第二象限,Fi>0,是-dx,如果在第一象限是+dx
dir_x = "-" if Xe<0 else "+"
dir_y = "-" if Ye<0 else "+"
"""
if rel_x <0:
dir_dx ="-dx"
else:
dir_dx = "+dx"
if rel_y <0:
dir_dy = "-dy"
else:
dir_dy = "+dy"
"""
Fi= [0] # 判别偏差
print("判别\\t\\t\\t进给\\t\\t\\t运算\\t\\t\\t比较\\t\\t\\t")
for i in range(n):
# 正偏差,位于直线上方
if Fi[i] >=0 :
dir = dir_x +"dx" # 往x正方向
print(Fi[-1],end="\\t\\t\\t")
F_temp = Fi[-1] - abs(Ye) # 迭代发偏差运算
x_temp = x[i] - 1 if Xe<0 else x[i]+1 # 记录下一个x坐标,x[i+1] = x[i]
y_temp = y[i] # 记录下一个y坐标,y[i+1] = y[i]
x.append(x_temp) # 对每一个x坐标进行储存
y.append(y_temp) # 对每一个y坐标进行储存
pos_temp = (x_temp,y_temp) # 对每一个坐标点进行储存
pos.append(pos_temp)
Fi.append(F_temp) # 对运算偏差进行存储
print(dir,end="\\t\\t\\t")
print(Fi[-1],end="\\t\\t\\t")
print(n-i)
else:
dir = dir_y+ "dy" # 往y正方向
print(Fi[-1],end="\\t\\t\\t")
print(dir,end="\\t\\t\\t")
F_temp =Fi[-1] + abs(Xe) # 迭代发偏差运算
y_temp = y[i]-1 if Ye<0 else y[i] +1 # 记录下一个y坐标,y[i+1] = y[i]+1
x_temp = x[i] # 记录下一个x坐标,其中x不变x[i+1] = x[i]
x.append(x_temp) # 对每一个x坐标进行储存
y.append(y_temp) # 对每一个y坐标进行储存
pos_temp =(x_temp,y_temp) # 对每一个坐标点进行储存
pos.append(pos_temp)
Fi.append(F_temp) # 对运算偏差进行存储
print(Fi[-1],end="\\t\\t\\t")
print(n-i)
# 画图
plt.plot([0,Xe],[0,Ye],color = 'r') # 起点、终点连线
plt.plot(x,y,'o',color='b') # 画点
plt.plot(x,y) # 画线
plt.savefig('.\\\\2.jpg')
plt.show()
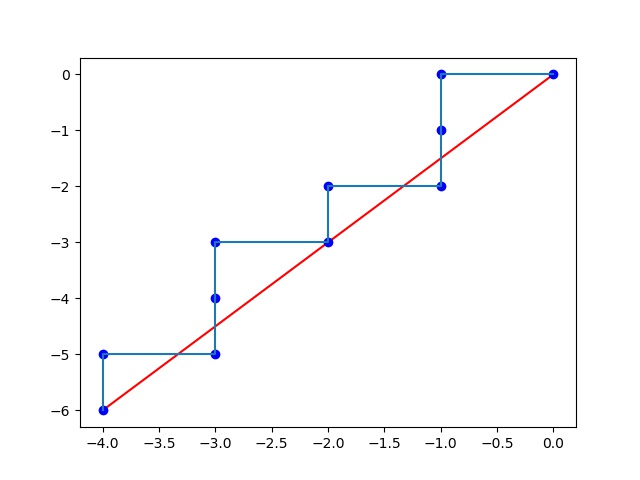
3.1.4 四象限直线插补代码运行效果
请输入直线起点坐标: -4,-5
请输入直线终点坐标: -8,-11
判别 进给 运算 比较
0 -dx -6 10
-6 -dy -2 9
-2 -dy 2 8
2 -dx -4 7
-4 -dy 0 6
0 -dx -6 5
-6 -dy -2 4
-2 -dy 2 3
2 -dx -4 2
-4 -dy 0 1
3.2 圆弧插补程序以及效果
3.2.1 第一象限圆弧插补程序
# -*- coding: cp936 -*-
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import math
# 通过键盘输入获取圆弧信息
print("当前进入的是圆心位于原点,圆弧位于第一象限情况")
pos_s = input("请输入圆弧起点:\\t")
pos_e = input("请输入圆弧的终点:\\t")
pos_s = pos_s.split(',') # 对开始坐标进行获取,3,4拆分下来就是x=3,y=4
pos_e = pos_e.split(',') # 对结束坐标进行获取
# 获取起点终点x,y值,以及总步数
Xs = int(pos_s[0])
Ys = int(pos_s[1])
Xe = int(pos_e[0])
Ye = int(pos_e[1])
n = abs(Xs-Xe)+abs(Ys-Ye)
# 定义列表用于储存需要计算以及打印的数据
Fi= [0] # 包括原点的偏差数据
x = [Xs] # 每个x坐标
y = [Ys] # 每个y坐标
pos = [(Xs,Ys)] # 每个点的坐标
dir = [] # 储存运动方向
div_cri = [] # Deviation criterion 误差判别>0/<0
str_Fi_list = [] # 将F+编号i生成一个字符串
new_dev_calc = [] # 用于储存新偏差数据eg:F1>0 New deviation calculation
# 对第一行信息进行打印
print("序号\\t\\t\\t偏差判别\\t\\t\\t进给\\t\\t\\t新偏差计算\\t\\t\\t坐标计算\\t\\t终点判别\\t\\t\\t")
print("\\t\\t\\t\\t\\t\\t", end="\\t\\t\\t\\t")
print("F0 =",Fi[-1],"\\t\\t\\t\\t",pos[-1],"\\t\\t")
# 插补算法的计算
for i in range(n):
# 逆时针加工
if Xs > Xe:
# 点位于圆外
if Fi[i]>=0:
str_Fi= 'F'+str(i+1) # 生成Fi
# 偏差计算、坐标计算
F_new = Fi[-1] - 2 * x[i] + 1 # 迭代发偏差运算
x_new= x[-1] - 1 # 记录下一个x坐标,x[i+1] = x[i]
y_new = y[-1] # 记录下一个y坐标,y[i+1] = y[i]
pos_new = (x_new, y_new) # 对每一个坐标点进行储存
F_new_str = str_Fi+" = "+str(F_new) # 新偏差公式
x.append(x_new) # 对每一个x坐标进行储存
y.append(y_new) # 对每一个y坐标进行储存
str_Fi_list.append(str_Fi) # 对F0,F1 等字符串进行储存
div_cri.append(str_Fi+">0") # 对偏差判别进行储存 Fi>0
dir.append("-dx") # 对进给方向进行储存 -dx
Fi.append(F_new) # 对新偏差进行存储 Fi
new_dev_calc.append(F_new_str) # 对新偏差计算结果公式进行储存 F0 = -5
pos.append(pos_new) # 对每一个心得坐标位置及逆行储存
else:
str_Fi = 'F' + str(i+1) # 生成Fi
F_new = Fi[-1] + 2 * y[i] + 1 # 迭代发偏差运算
x_new = x[-1] # 记录下一个x坐标,x[i+1] = x[i]
y_new = y[-1] + 1 # 记录下一个y坐标,y[i+1] = y[i]
pos_temp = (x_new, y_new) # 对每一个坐标点进行储存
F_temp_str = str_Fi+" = "+str(F_new) # 新偏差公式
x.append(x_new) # 对每一个x坐标进行储存
y.append(y_new) # 对每一个y坐标进行储存
str_Fi_list.append(str_Fi) # 对F0,F1 等字符串进行储存
div_cri.append(str_Fi+"<0") # 对偏差判别进行储存 Fi>0
dir.append("+dy") # 对进给方向进行储存 -dx
Fi.append(F_new) # 对新偏差进行存储 Fi
new_dev_calc.append(F_temp_str) # 对新偏差计算结果公式进行储存 F0 = -5
pos.append(pos_temp) # 对每一个心得坐标位置及逆行储存
# 顺时针运算
else:
# 点位于圆外
if Fi[i] >= 0:
str_Fi = 'F' + str(i +以上是关于2021-10-17的主要内容,如果未能解决你的问题,请参考以下文章