Logistic 回归
Posted lhys666
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Logistic 回归相关的知识,希望对你有一定的参考价值。
Logistic 回归
创作背景
本菜鸡最近想学学 机器学习,这不,刚开始。
如果觉得我这篇文章写的好的话,能不能给我 点个赞 ,评论 一波。如果要点个 关注 的话也不是不可以🤗
回归与分类的区别
- 回归 要预测的结果是 具体的数值,根据训练数据预测某一输入对应的输出数据。输出的结果是 实数。
- 分类 要判断的结果是 类别,根据训练数据预测 分类正确的概率 (属于
[0, 1]),进而输出 判断的类别 。
回归向分类的转变
既然都是 预测,使用相同的 x ,只是输出从原来的 实数 变成了 类别,那我们就用一个函数将结果从 实数集 映射到 [0, 1] 中,然后再转成对应分类不就行了呗。
- 举个栗子:
- 有两个类别的实例,
o代表正例,x代表负例 - 可以找到一个超平面
w
T
x
+
b
=
0
{w}^{T}x+b=0
wTx+b=0 将两类实例分隔开,即
正确分类 - 其中,
w
∈
R
n
w \\in {\\mathbb{R}}^{n}
w∈Rn 为超平面的
法向量, b ∈ R b \\in \\mathbb{R} b∈R 为偏置 - 超平面上方的点都满足 w T x + b > 0 {w}^{T}x+b>0 wTx+b>0
- 超平面下方的点都满足 w T x + b < 0 {w}^{T}x+b<0 wTx+b<0
- 可以根据以下
x的线性函数值(与 0 的比较结果)判断实例类别: z = g ( x ) = w T x + b z=g(x)={w}^{T}x+b z=g(x)=wTx+b - 分类函数以
z为输入,输出预测的类别: c = H ( z ) = H ( g ( x ) ) c=H(z)=H(g(x)) c=H(z)=H(g(x))
- 有两个类别的实例,
- 以上是 线性分类器 的基本模型。
有个方法可以实现 线性分类器 ,那就是 Logistic 回归。
Logistic回归是一种 广义线性 模型,使用 线性判别式函数 对实例进行分类。
而一般实现这种分类方法的函数是 sigmoid 函数。(因为其中最为出名的是 logistic 函数,所以也被称为 logistic 函数)。
饱和函数
先看一下 饱和函数,至于为什么要看这个函数,因为 Sigmoid 函数都需要满足这个函数,具体见下述 sigmoid (也即 logistic) 函数。
x < 0时,导数值↑,x ≥ 0时,导数值↓,即,将导函数为 正态分布 的分布函数称为 饱和函数 。- 看一下图像。
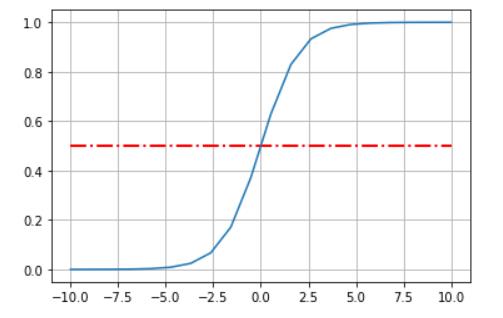
一些饱和函数
- 单位阶跃函数
δ - e r f ( π 2 x ) erf(\\frac{\\sqrt {\\pi}}{2}x) erf(2πx)
- 2 π arctan ( π 2 x ) \\frac{2}{\\pi} \\arctan {(\\frac{\\pi}{2}x)} π2arctan(2πx)
- 2 π g d ( π 2 x ) \\frac{2}{\\pi} gd(\\frac{\\pi}{2}x) π2gd(2πx)
- x 1 + ∣ x ∣ \\frac{x}{1+|x|} 1+∣x∣x
图像如下
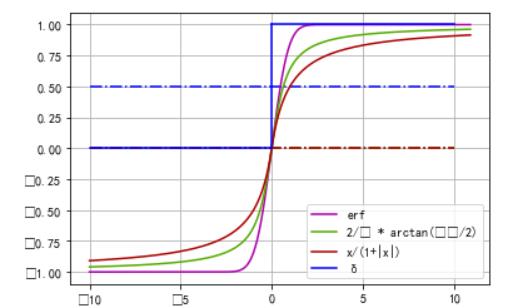
它们的导函数是服从 正态分布 的,图像如下
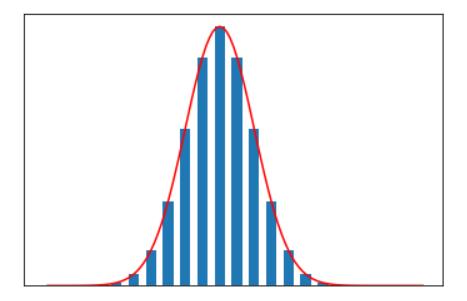
所以,最理想的分类函数为 单位阶跃函数 ,直上直下的,是 饱和函数 的一种。如下图
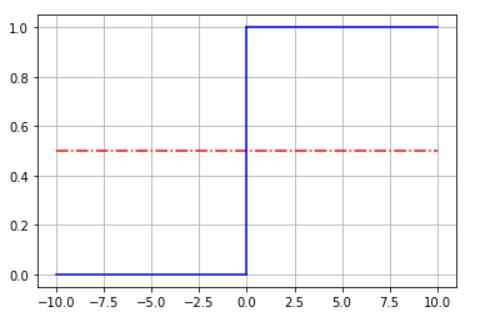
也就是
H
(
z
)
=
{
0
,
x
<
0
0.5
,
x
=
0
1
,
x
>
0
H(z)= \\begin{cases} 0, x<0 \\\\ 0.5, x=0 \\\\ 1, x>0 \\end{cases}
H(z)=⎩⎪⎨⎪⎧0,x<00.5,x=01,x>0
- 但单位阶跃函数作为分类函数有一个严重缺点,不连续,所以 不是处处可微,使得一些算法不可用(如 梯度下降)。
- 找一个 输入输出特性与单位阶跃函数类似,并且 单调可微的函数 来代替阶跃函数,
sigmoid函数是一种常用替代函数。
sigmoid 函数(logistic 函数)
sigmoid 函数是一类函数,满足以下函数特征即可:
- 有极限
- 单调 增 函数
- 满足 饱和函数 (知道我为什么要提到 饱和函数 了吧(●’◡’●))
函数定义
σ
(
x
)
=
1
1
+
e
−
z
\\sigma(x)=\\frac{1}{1+{e}^{-z}}
σ(x)=1+e−z1
- 一般
σ
\\sigma
σ 函数就指
logistic函数
logistic 函数的值域在 (0,1) 之间连续,函数的输出可视为 x 条件下实例为正例的条件概率 ,即
P
(
y
=
1
∣
x
)
=
σ
(
g
(
x
)
)
=
1
1
+
e
−
(
w
T
x
+
b
)
P(y=1|x)=\\sigma (g(x))=\\frac{1}{1+{e}^{-({w}^{T}x+b)}}
P(y=1∣x)=σ(g(x))=1+e−(wTx+b)1
x 条件下实例为负例的条件概率为
P
(
y
=
0
∣
x
)
=
1
−
σ
(
g
(
x
)
)
=
1
1
+
e
(
w
T
x
+
b
)
P(y=0|x)=1-\\sigma (g(x))=\\frac{1}{1+{e}^{({w}^{T}x+b)}}
P(y=0∣x)=1−σ(g(x))=1+e(wTx+b)1
logistic 函数是 对数概率函数 的 反函数,一个事件的概率指该事件发生的概率 p 与该事件不发生的概率 1-p 的比值。
- 对数概率为
log p 1 − p \\log{\\frac{p}{1-p}} log1−pp - 对数概率大于 0 表明 正例 的概率大,反之,则 负例 的概率大。
Logistic 回归模型假设一个实例为正例的对数概率是输入 x 的 线性函数,即:
log
p
1
−
p
=
w
T
x
+
b
\\log {\\frac{p}{1-p}}={w}^{T}x+b
log1−pp=wTx+b
反求 p ,即:
p
=
σ
(
g
(
x
)
)
=
1
1
+
e
−
(
w
T
x
+
b
)
p = \\sigma(g(x))=\\frac{1}{1+{e}^{-({w}^{T}x+b)}}
p=σ(g(x))=1+e−(wTx+b)1
logistic 函数有个很好的数学特性,
σ
(
z
)
\\sigma(z)
σ(z) 一阶导数形式简单,并且关于其本身的函数:
d
σ
(
z
)
d
z
=
σ
(
z
)
(
1
−
σ
(
z
)
)
\\frac{d \\sigma(z)}{dz} = \\sigma(z) (1-\\sigma(z))
dzdσ(z)=σ(z)(1−σ(z))
Logistic 回归模型假设函数为
h
w
,
b
(
x
)
=
σ
(
g
(
x
)
)
=
1
1
+
e
−
(
w
T
x
+
b
)
{h}_{w,b}(x) = \\sigma (g(x)) = \\frac{1}{1+{e}^{-({w}^{T}x+b)}}
hw,b(x)=σ(g(x以上是关于Logistic 回归的主要内容,如果未能解决你的问题,请参考以下文章