因果推断笔记——DML ：Double Machine Learning案例学习（十六）
Posted 悟乙己
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了因果推断笔记——DML ：Double Machine Learning案例学习（十六）相关的知识，希望对你有一定的参考价值。
1 背景知识
参考：
Hetergeneous Treatment Effect旨在量化实验对不同人群的差异影响，进而通过人群定向/数值策略的方式进行差异化实验，或者对实验进行调整。Double Machine Learning把Treatment作为特征，通过估计特征对目标的影响来计算实验的差异效果。
Machine Learning擅长给出精准的预测，而经济学更注重特征对目标影响的无偏估计。DML把经济学的方法和机器学习相结合，在经济学框架下用任意的ML模型给出特征对目标影响的无偏估计，有知乎大佬的一个总结：
HTE问题可以用以下的notation进行简单的抽象
- Y是实验影响的核心指标
- T是treatment，通常是0/1变量，代表样本进入实验组还是对照组，对随机AB实验T⊥X
- X是Confounder，可以简单理解为未被实验干预过的用户特征，通常是高维向量
- DML最终估计的是θ(x)，也就是实验对不同用户核心指标的不同影响
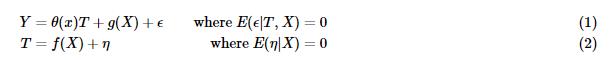
最直接的方法就是用X和T一起对Y建模，直接估计θ(x)。
但这样估计出的θ(x)往往是有偏的，偏差部分来自于对样本的过拟合，部分来自于g(X)估计的偏差，假定θ0是参数的真实值，则偏差如下：
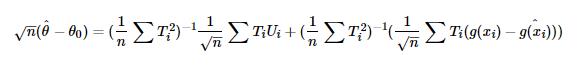
2 DML Dynamic Double Machine Learning
【因果推断/uplift建模】Double Machine Learning(DML)
2.1 DML训练过程
参考：AB实验人群定向HTE模型4 - Double Machine Learning
训练的过程：
步骤一. 用任意ML模型拟合Y和T得到残差Y ,T
比较常见的是使用lasso / RF进行E(Y|x)的估计
步骤二. 对Y,T用任意ML模型拟合θ
θ(X)的拟合可以是参数模型也可以是非参数模型，参数模型可以直接拟合。而非参数模型因为只接受输入和输出所以需要再做如下变换，模型Target变为Y/T, 样本权重为T^2
步骤三. Cross-fitting
这个Cross-fitting步骤非常重要，DML保证估计无偏很重要的一步就是Cross-fitting，用来降低overfitting带来的估计偏差。先把总样本分成两份：样本1，样本2。
先用样本1估计残差，样本2估计θ1，再用样本2估计残差，样本1估计θ2，取平均得到最终的估计。当然也可以进一步使用K-Fold来增加估计的稳健性。
Jonas在他的博客里比较了不使用DML，使用DML但是不用Cross-fitting，以及使用Cross-fitting的估计效果如下：
2.2 HTL无偏估计
直观角度上，这里对回归比较熟悉的朋友可以知道，线性回归是拟合Y在特征空间X的最佳投影（既误差最小化），所以残差是垂直样本空间X的，既最大限度消除了（独立）X的相关性！如下图所示。
关于残差正交化可得到无偏差因果效应的数学原理：https://zhuanlan.zhihu.com/p/41993542
2.3 使用DML估计ATE
具体到因果推断的例子上，我们只关心Treatment T 对 outcome Y的影响，因此我们可以首先使用X回归T，得到一个T的残差（实际T - 预测T），然后使用X回归Y，得到一个Y的残差（实际Y - 预测Y），最后使用T的残差回归Y的残差，估计的参数即我们想要的ATE。
( Y − ( Y ∼ X ) ) ∼ ( T − ( T ∼ X ) ) (Y - (Y \\sim X)) \\sim (T - (T \\sim X)) (Y−(Y∼X))∼(T−(T∼X))
Y i − E [ Y i ∣ X i ] = τ ⋅ ( T i − E [ T i ∣ X i ] ) + ϵ Y_i - E[Y_i | X_i] = \\tau \\cdot (T_i - E[T_i | X_i]) + \\epsilon Yi−E[Yi∣Xi]=τ⋅(Ti−E[Ti∣Xi])+ϵ
于是乎，具体的DML方法也就出来了，其核心思想即分别用机器学习算法基于X预测T和Y，然后使用T的残差回归Y的残差：
Y i − M ^ y ( X i ) = τ ⋅ ( T i − M ^ t ( X i ) ) + ϵ Y_i - \\hat{M}_y(X_i) = \\tau \\cdot (T_i - \\hat{M}_t(X_i)) + \\epsilon Yi−M^y(Xi)=τ⋅(Ti−M^t(Xi))+ϵ
其中， M ^ y ( X i ) \\hat{M}_y(X_i) M^y(Xi) 建模 E [ Y ∣ X ] E[Y|X] E[Y∣X] ， M ^ t ( X i ) \\hat{M}_t(X_i) M^t(Xi) 建模 E [ T ∣ X ] E[T|X] E[T∣X]。
那么问题来了，为什么说DML能去偏呢？
其关键在于 M ^ t ( X i ) \\hat{M}_t(X_i) M^t(Xi)，它对Treatment实施了去偏。T的残差可以看作将X对T的作用从T中去除后剩下的量，此时T的残差独立于X。
而 M ^ y ( X i ) \\hat{M}_y(X_i) M^y(Xi)的作用在于去除Y的方差，即将X引起的Y的方差从Y中去除。
最后，我们再对残差建模lr，即得到ATE。
2.4 使用DML估计CATE
同样地，我们首先基于X使用ML获得T的残差和Y的残差，之后使用lr拟合残差，不同的是，这次我们把X和T的交互项加进来，即
Y i − M y ( X i ) = τ ( X i ) ⋅ ( T i − M t ( X i ) ) + ϵ i Y_i - {M}_y(X_i) = \\tau(X_i) \\cdot (T_i - {M}_t(X_i)) + \\epsilon_i Yi−My(Xi)=τ(Xi)⋅(Ti−Mt(Xi))+ϵi
Y i ~ = α + β 1 T i ~ + β 2 X i T i ~ + ϵ i \\tilde{Y_i} = \\alpha + \\beta_1 \\tilde{T_i} + \\pmb{\\beta}_2 \\pmb{X_i} \\tilde{T_i} + \\epsilon_i Yi~=α+β1Ti~+βββ2XiXiXiTi~+ϵi
然后我们就可以计算CATE的值了：
μ ^ ( ∂ S a l e s i , X i ) = M ( P r i c e = 1 , X i ) − M ( P r i c e = 0 , X i ) \\hat{\\mu}(\\partial Sales_i, X_i) = M(Price=1, X_i) - M(Price=0, X_i) μ^(∂Salesi,Xi)=M(Price=1,Xi)−M(Price=0,Xi)
其中，M即最后的lr模型。
2.5 直接预测反事实的Y
在处理非线性CATE时，另一种方案是我们将不再尝试估计CATE的线性近似。相反，我们将做出反事实的预测。
(这种方案在实际中使用也很多，但并没有严格的理论证明！)
其流程分为两个步骤：
第一步，依然是估计T和Y的残差：
Y
~
i
=
τ
(
X
i
)
T
~
i
+
e
i
\\tilde{Y}_i = \\tau(X_i) \\tilde{T}_i + e_i
以上是关于因果推断笔记——DML ：Double Machine Learning案例学习（十六）的主要内容，如果未能解决你的问题，请参考以下文章 因果推断与反事实预测——利用DML进行价格弹性计算（二十四） 因果推断与反事实预测——利用DML进行价格弹性计算（二十四） 因果推断与反事实预测——利用DML进行价格弹性计算（二十三） 因果推断——借微软EconML测试用DML和deepIV进行反事实预测实验（二十五）