初步认识零基础算法
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了初步认识零基础算法相关的知识,希望对你有一定的参考价值。
前言
我大学的时候比较疯狂,除了上课的时候,基本都是在机房刷题,当然,有时候连上课都在想题目,纸上写好代码,一下课就冲进机房把代码敲了,目的很单纯,为了冲排行榜,就像玩游戏一样,享受霸榜的快感。
当年主要是在 「 杭电OJ 」 和 「 北大OJ 」 这两个在线平台上刷题,那时候还没有(「 LeetCode 」、「 牛客 」、「 洛谷 」 这些先如今非常🔥的刷题网站),后来参加工作以后,剩余的时间不多了,也就没怎么刷了, 但是 「 算法思维 」 也就是靠上大学那「 四年 」锻炼出来的。
当年题目少,刷题的人也少,所以勉强还冲到过第一,现在去看已经 58 名了,可见 「 长江后浪推前浪 」,前浪 S 在沙滩上。时势造英雄啊!
北大人才辈出,相对题目也比较难,所以明显有点 「 心有余而力不足 」 的感觉,刷的相对就少很多,而且这个 OJ 也没什么人维护了,看我的签名,当时竟然还想着给博客引点流,现在估计都没什么人去那个网站了吧。
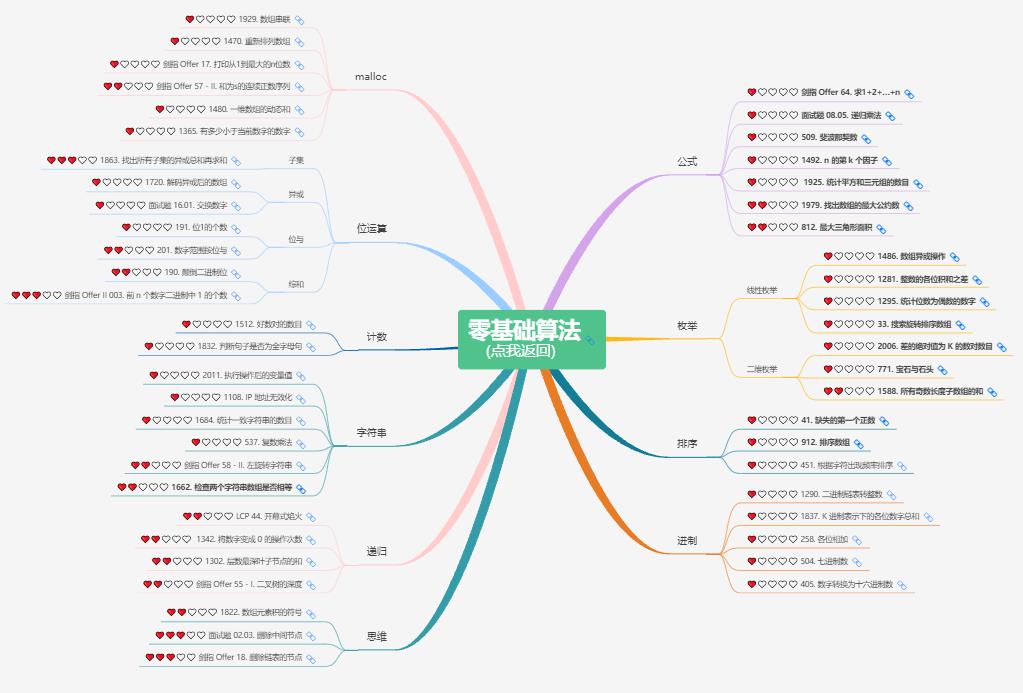
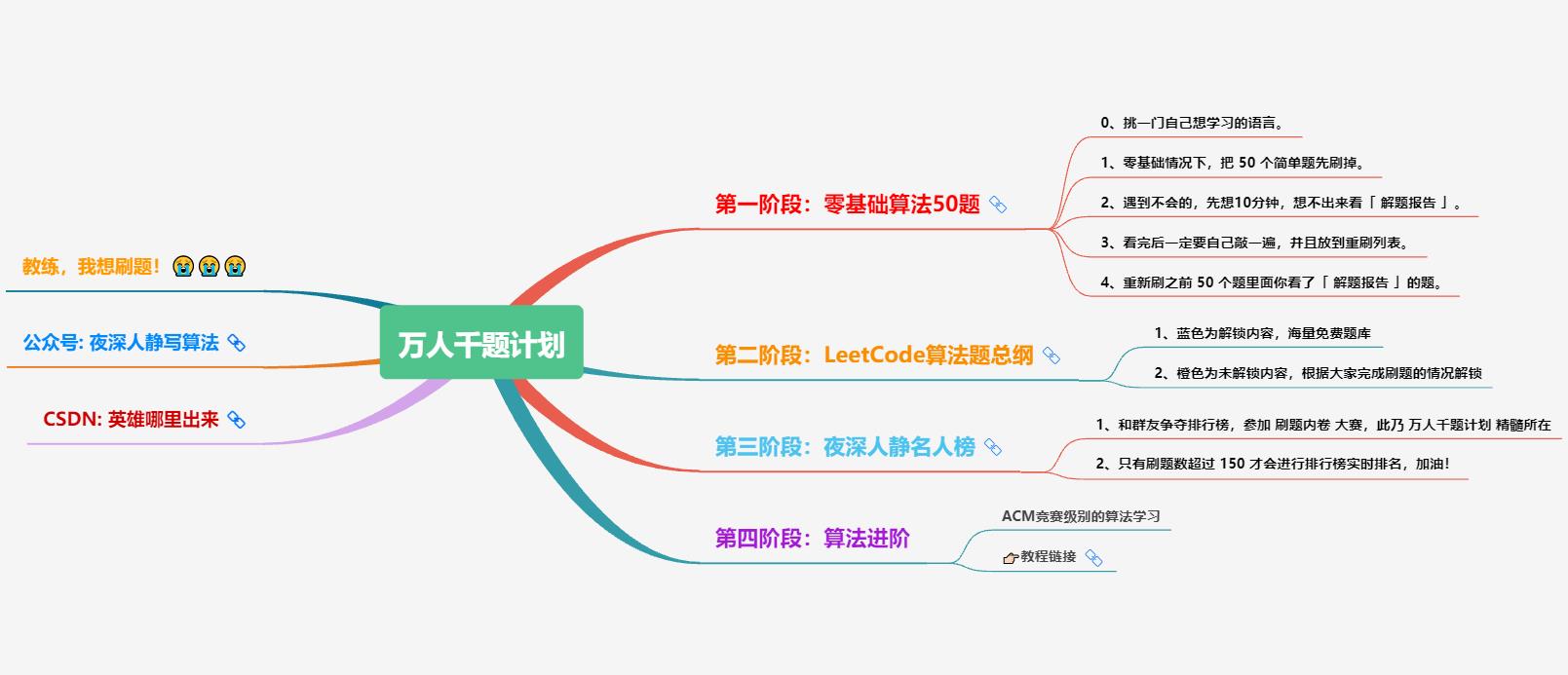
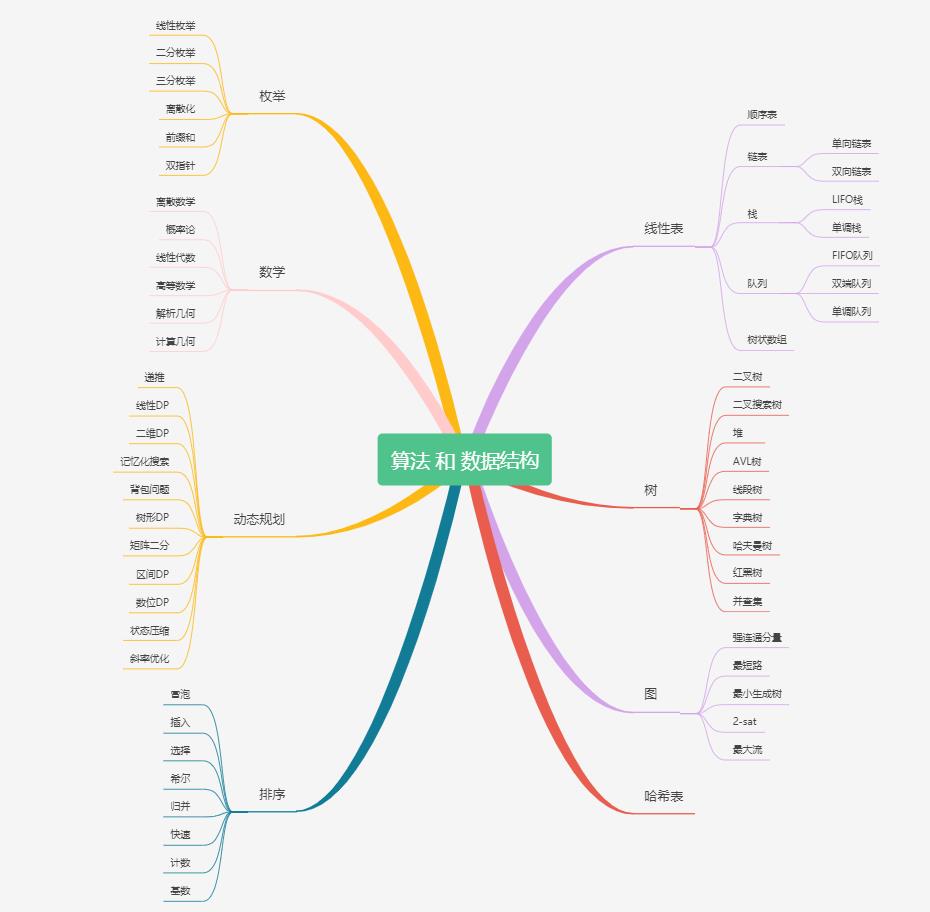
这篇文章的主要目的是为尚未接触算法的朋友提供一个学习算法的路线指引,但是实际学习过程还是需要看个人的毅力和坚持。那么,让我们先来看下需要按照什么样的顺序来进行刷题吧。下图代表的是 LeetCode 经典的算法和数据结构的总纲。
点击我跳转末尾 获取 粉丝专属 《算法和数据结构》源码,以及获取博主的联系方式。
文章目录
一、算法
1、排序
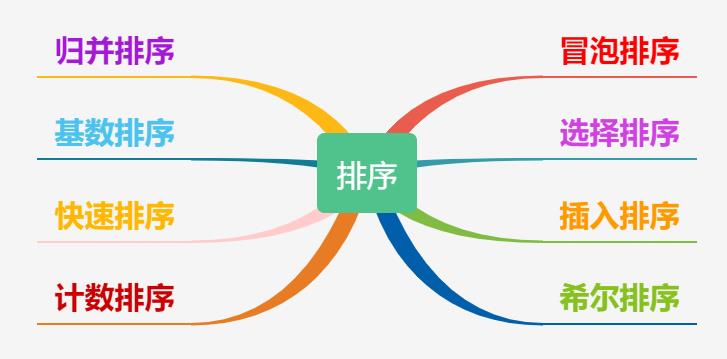
1)冒泡排序
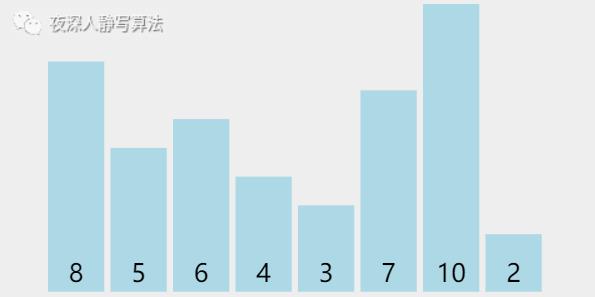
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表正在执行比较的两个数 |
| ■ 的柱形 | 代表已经排好序的数 |
我们看到,首先需要将 「第一个元素」 和 「第二个元素」 进行 「比较」,如果 前者 大于 后者,则进行 「交换」,然后再比较 「第二个元素」 和 「第三个元素」 ,以此类推,直到 「最大的那个元素」 被移动到 「最后的位置」 。
然后,进行第二轮「比较」,直到 「次大的那个元素」 被移动到 「倒数第二的位置」 。
最后,经过一定轮次的「比较」 和 「交换」之后,一定可以保证所有元素都是 「升序」 排列的。
2)选择排序
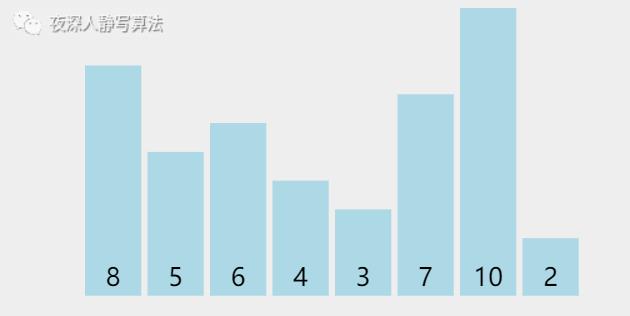
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表正在执行 比较 的数 |
| ■ 的柱形 | 代表已经排好序的数 |
| ■ 的柱形 | 有两种:1、记录最小元素 2、执行交换的元素 |
我们发现,首先从 「第一个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」,和 「第一个元素」 进行 「交换」;
然后,从 「第二个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」,和 「第二个元素」 进行 「交换」。
最后,一定可以保证所有元素都是 「升序」 排列的。
3)插入排序

| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表正在执行 比较 和 移动 的数 |
| ■ 的柱形 | 代表已经排好序的数 |
| ■ 的柱形 | 代表待执行插入的数 |
我们看到,首先需要将 「第二个元素」 和 「第一个元素」 进行 「比较」,如果 前者 小于等于 后者,则将 后者 进行向后 「移动」,前者 则执行插入;
然后,进行第二轮「比较」,即 「第三个元素」 和 「第二个元素」、「第一个元素」 进行 「比较」, 直到 「前三个元素」 保持有序 。
最后,经过一定轮次的「比较」 和 「移动」之后,一定可以保证所有元素都是 「升序」 排列的。
4)希尔排序
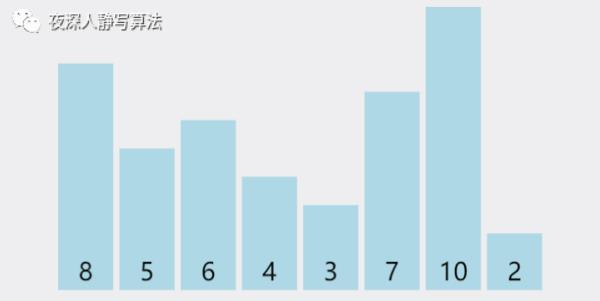
一下子看完不是很理解,没有关系,我们把这几个过程分拆开来。第一趟分解后,如图所示:
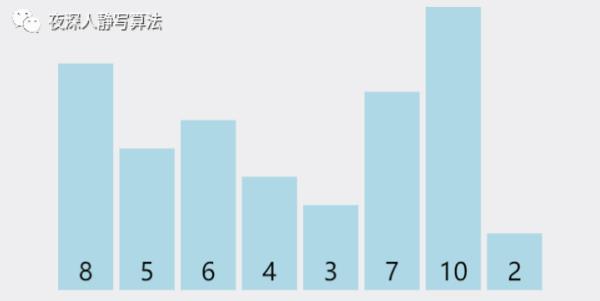
增量为 4,所有元素总共分为 4 组,分别为 [8, 3]、[5, 7]、[6, 10]、[4, 2],同组内部分别执行插入排序,得到 [3, 8]、[5, 7]、[6, 10]、[2, 4](由于每组只有两个元素,所以升序的情况位置不变,降序的情况执行组内元素位置交换,抖动一下代表保持原顺序不变,有一种 “我不换 ~~ 我不换” 的意思在里面 )。
第二趟分解后,如图所示:
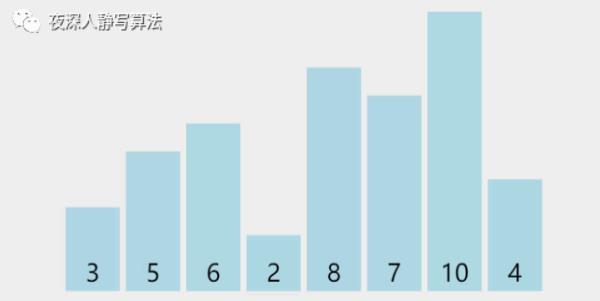
增量为 2,所有元素总共分为 2 组,分别为 [3, 6, 8, 10]、[5, 2, 7, 4],同组内部分别执行插入排序,[3, 6, 8, 10]已经升序,保持原样;[5, 2, 7, 4] 执行三次插入排序后变成 [2, 4, 5, 7]。
第三趟分解后,如图所示:
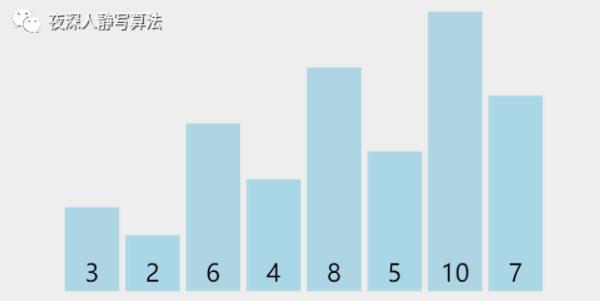
增量为 1,所有元素归为 1 组,为 [3, 2, 6, 4, 8, 5, 10, 7]。对它执行简单插入排序,执行完毕后,必然可以保证所有元素有序。
5)归并排序
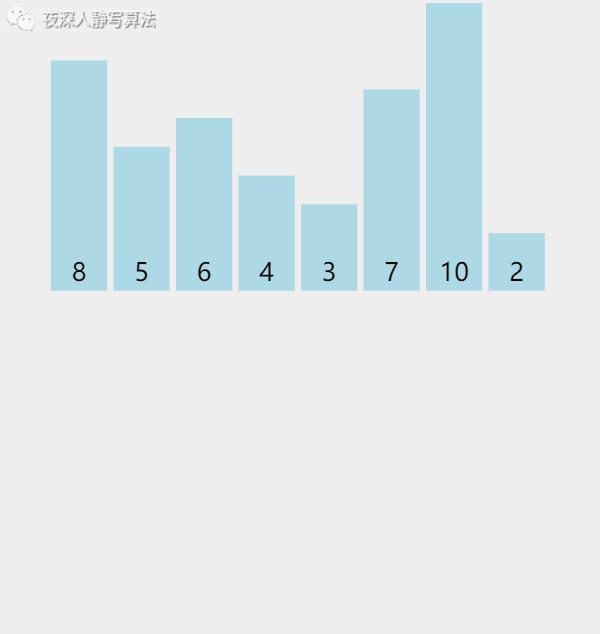
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表已经排好序的数 |
| 其他颜色 ■ 的柱形 | 正在递归、归并中的数 |
我们发现,首先将 「 8个元素 」 分成 「 4个元素 」,再将 「 4个元素 」 分成 「 2个元素 」,然后 「比较」这「 2个元素 」的值,使其在自己的原地数组内有序,然后两个 「 2个元素 」 的数组归并变成 「 4个元素 」 的 「升序」数组,再将两个「 4个元素 」 的数组归并变成 「 8个元素 」 的 「升序」数组。
6)快速排序
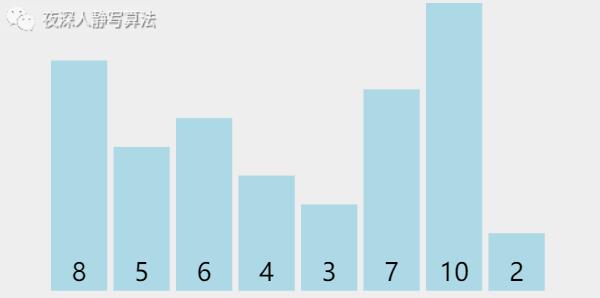
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表随机选定的基准数 |
| ■ 的柱形 | 代表已经排序好的数 |
| ■ 的柱形 | 代表正在遍历比较的数 |
| ■ 的柱形 | 代表比基准数小的数 |
| ■ 的柱形 | 代表比基准数大的数 |
我们发现,首先随机选择了一个 7 作为「 基准数 」,并且将它和最左边的数交换。然后往后依次遍历判断,小于 7 的数为 「 绿色 」 ,大于 7 的数为「 紫色 」,遍历完毕以后,将 7 和 「 下标最大的那个比 7 小的数 」交换位置,至此,7的左边位置上的数都小于它,右边位置上的数都大于它,左边和右边的数继续递归求解即可。
7)计数排序
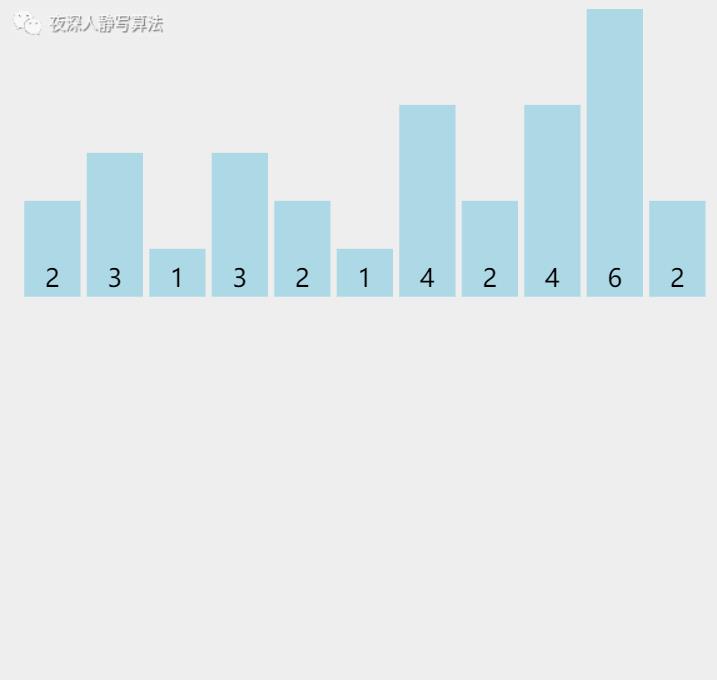
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 计数为 0 的数 |
| ■ 的柱形 | 计数为 1 的数 |
| ■ 的柱形 | 计数为 2 的数 |
| ■ 的柱形 | 计数为 3 的数 |
| ■ 的柱形 | 计数为 4 的数 |
我们看到,首先程序生成了一个区间范围为
[
1
,
9
]
[1, 9]
[1,9] 的 「 计数器数组 」,并且一开始所有值的计数都为 0。
然后,遍历枚举「 原数组 」的所有元素,在 元素值 对应的计数器上执行 「 计数 」 操作。
最后,遍历枚举「 计数器数组 」,按照数组中元素个数放回到 「 原数组 」 中。这样,一定可以保证所有元素都是 「升序」 排列的。
8)基数排序

「 红色的数字位 」 代表需要进行 「 哈希 」 映射到给定 「 队列 」 中的数字位。
我们看到,首先程序生成了一个区间范围为
[
0
,
9
]
[0, 9]
[0,9] 的 「 基数队列 」。
然后,总共进行了 4 轮「 迭代 」(因为最大的数总共 4 个数位)。
每次迭代,遍历枚举 「 原数组 」 中的所有数,并且取得本次迭代对应位的数字,通过「 哈希 」,映射到它「 对应的队列 」中 。然后将 「 队列 」 中的数据按顺序塞回 「 原数组 」 完成一次「 迭代 」,4 次「 迭代 」后,一定可以保证所有元素都是 「升序」 排列的。
2、枚举
1)线性枚举
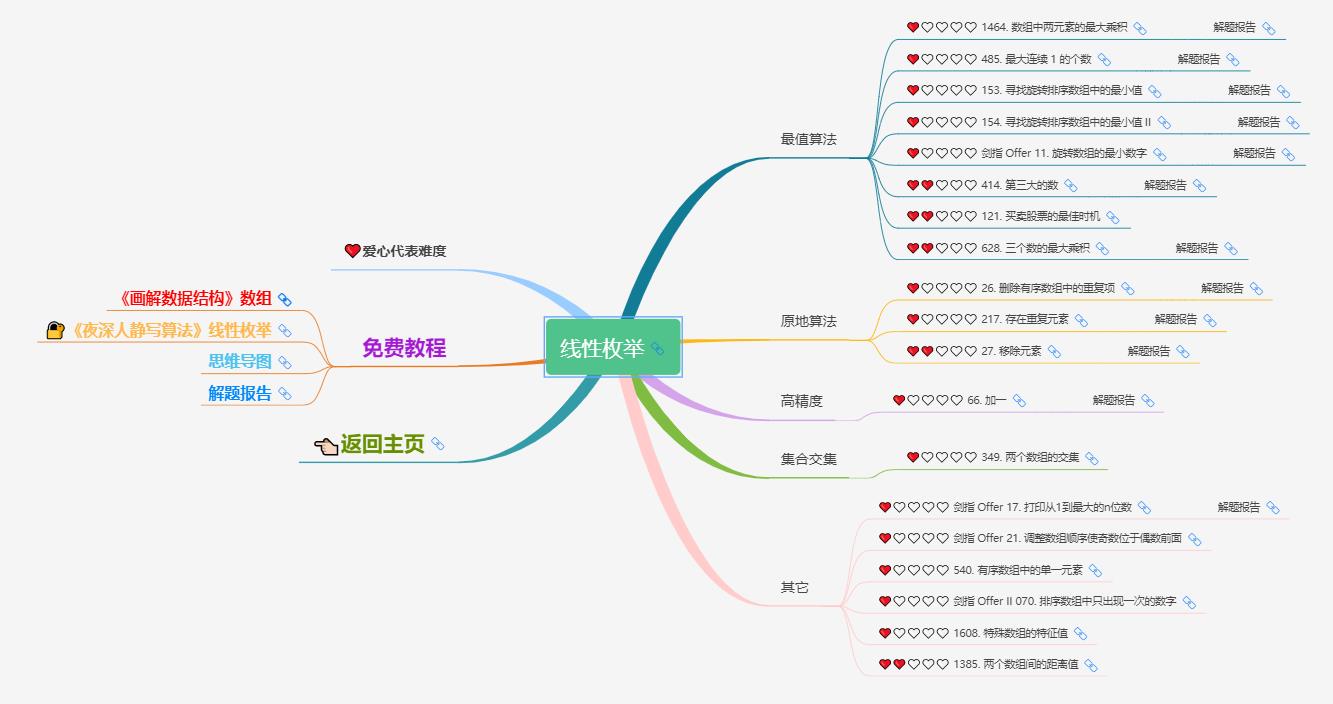
线性枚举,一般配合的 数据结构 是 【数组】 或者 【链表】,实现方式就是一个循环。正因为只有一个循环,所以线性枚举解决的问题一般比较简单,而且很容易从题目中看出来。
编写一个函数,将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
样例输入: [ “ a ” , “ b ” , “ c ” , “ d ” ] [“a”, “b”, “c”, “d”] [“a”,“b”,“c”,“d”]
样例输出: [ “ d ” , “ c ” , “ b ” , “ a ” ] [ “d”, “c”, “b”, “a”] [“d”,“c”,“b”,“a”]
原题出处: LeetCode 344. 反转字符串
翻转的含义,相当于就是 第一个字符 和 最后一个交换,第二个字符 和 最后第二个交换,… 以此类推,所以我们首先实现一个交换变量的函数 swap,然后再枚举 第一个字符、第二个字符、第三个字符 …… 即可。
对于第
i
i
i 个字符,它的交换对象是 第
l
e
n
−
i
−
1
len-i-1
len−i−1 个字符 (其中
l
e
n
len
len 为字符串长度)。swap函数的实现,可以参考:《C语言入门100例》 - 例2 | 交换变量。
线性枚举的过程为
O
(
n
)
O(n)
O(n),交换变量为
O
(
1
)
O(1)
O(1),两个过程是相乘的关系,所以整个算法的时间复杂度为
O
(
n
)
O(n)
O(n)。
class Solution {
public:
void swap(char& a, char& b) { // (1)
char tmp = a;
a = b;
b = tmp;
}
void reverseString(vector<char>& s) {
int len = s.size();
for(int i = 0; i < len / 2; ++i) { // (2)
swap(s[i], s[len-i-1]);
}
}
};
-
(
1
)
(1)
(1) 实现一个变量交换的函数,其中
&是C++中的引用,在函数传参是经常用到,被称为:引用传递(pass-by-reference),即被调函数的形式参数虽然也作为局部变量在堆栈中开辟了内存空间
,但是这时存放的是由主调函数放进来的实参变量的地址。被调函数对形参的任何操作都被处理成间接寻址,即通过堆栈中存放的地址访问主调函数中的实参变量。
简而言之,函数调用的参数,可以传引用,从而使得函数返回时,传参值的改变依旧生效。
- ( 2 ) (2) (2) 这一步是做的线性枚举,注意枚举范围是 [ 0 , l e n / 2 − 1 ] [0, len/2-1] [0,len/2−1]。
2)二分枚举
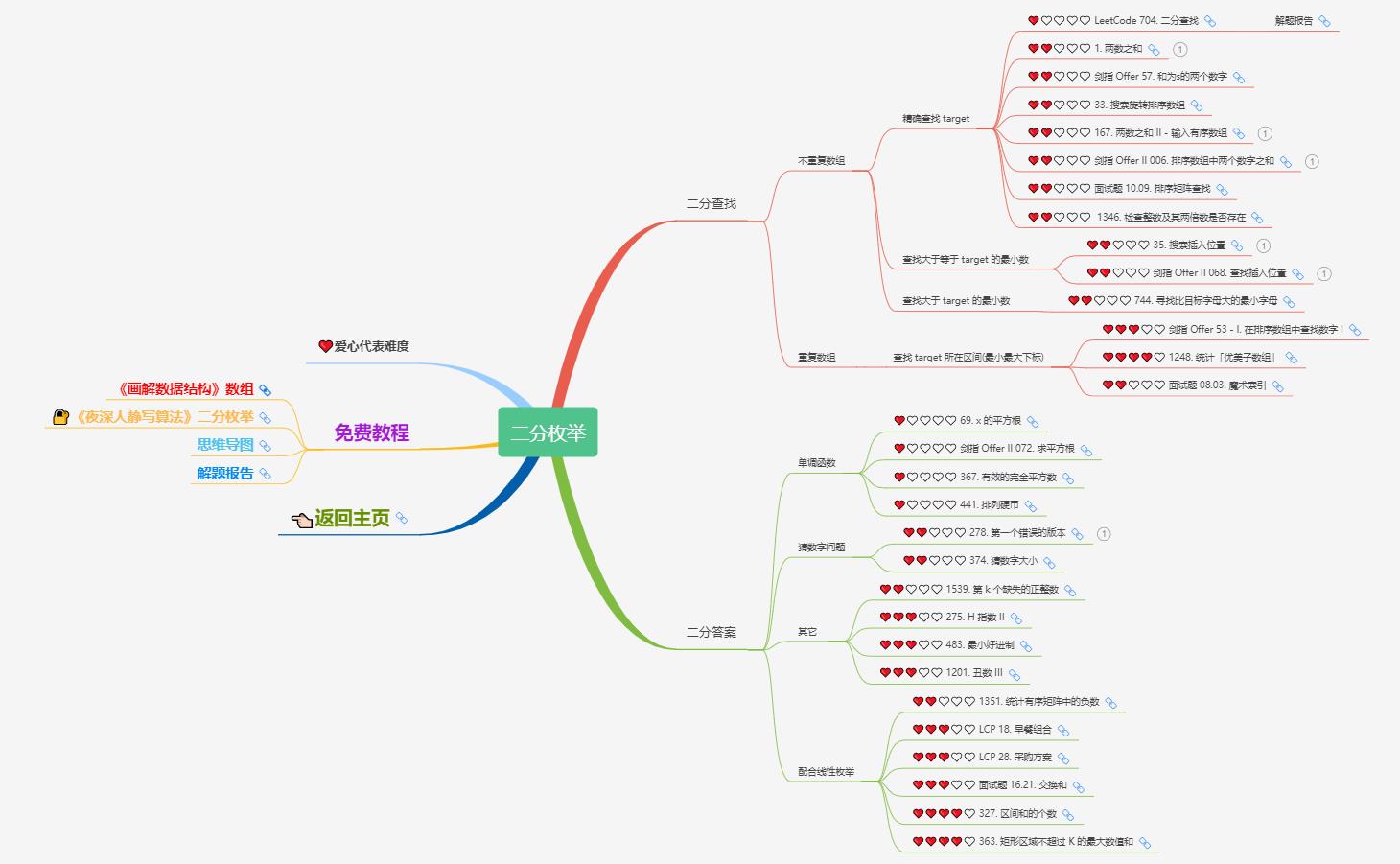
能用二分枚举的问题,一定可以用线性枚举来实现,只是时间上的差别,二分枚举的时间复杂度一般为对数级,效率上会高不少。同时,实现难度也会略微有所上升。我们通过平时开发时遇到的常见问题来举个例子。
软件开发的时候,会有版本的概念。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。假设你有 n n n 个版本 [ 1 , 2 , . . . , n ] [1, 2, ..., n] [1,2,...,n],你想找出导致之后所有版本出错的第一个错误的版本。可以通过调用
bool isBadVersion(version)接口来判断版本号version是否在单元测试中出错。实现一个函数来查找第一个错误的版本。应该尽量减少对调用 API 的次数。
样例输入: 5 5 5 和 b a d = 4 bad = 4 bad=4
样例输出: 4 4 4
原题出处: LeetCode 278. 第一个错误的版本
由题意可得,我们调用它提供的 API 时,返回值分布如下:
000...000111...111
000...000111...111
000...000111...111其中 0 代表false,1 代表true;也就是一旦出现 1,就再也不会出现 0 了。所以基于这思路,我们可以二分位置;
归纳总结为 2 种情况,如下:
1)当前二分到的位置 m i d mid mid,给出的版本是错误,那么从当前位置以后的版本不需要再检测了(因为一定也是错误的),并且我们可以肯定,出错的位置一定在 [ l , m i d ] [l, mid] [l,mid];并且 m i d mid mid 是一个可行解,记录下来;
2)当前二分到的位置 m i d mid mid,给出的版本是正确,则出错位置可能在 [ m i d + 1 , r ] [mid+1, r] [mid+1,r];
由于每次都是将区间折半,所以时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)。
class Solution {
public:
int firstBadVersion(int n) {
long long l = 1, r = n; // (1)
long long ans = (long long)n + 1;
while(l <= r) {
long long mid = (l + r) / 2;
if( isBadVersion(mid) ) {
ans = mid; // (2)
r = mid - 1;
}else {
l = mid + 1; // (3)
}
}
return ans;
}
};
-
(
1
)
(1)
(1) 需要这里,这里两个区间相加可能超过
int,所以需要采用 64 位整型long long; - ( 2 ) (2) (2) 找到错误版本的嫌疑区间 [ l , m i d ] [l, mid] [l,mid],并且 m i d mid mid 是确定的候选嫌疑位置;
- ( 3 ) (3) (3) 错误版本不可能落在 [ l , m i d ] [l, mid] [l,mid],所以可能在 [ m i d + 1 , r ] [mid+1, r] [mid+1,r],需要继续二分迭代;
3)三分枚举
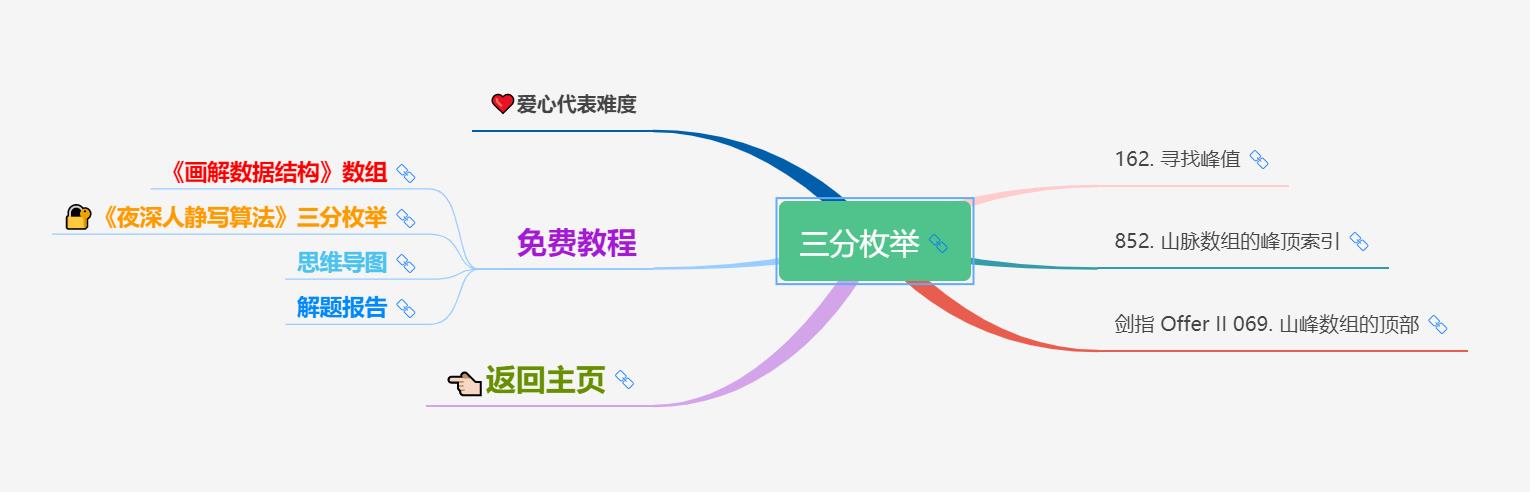
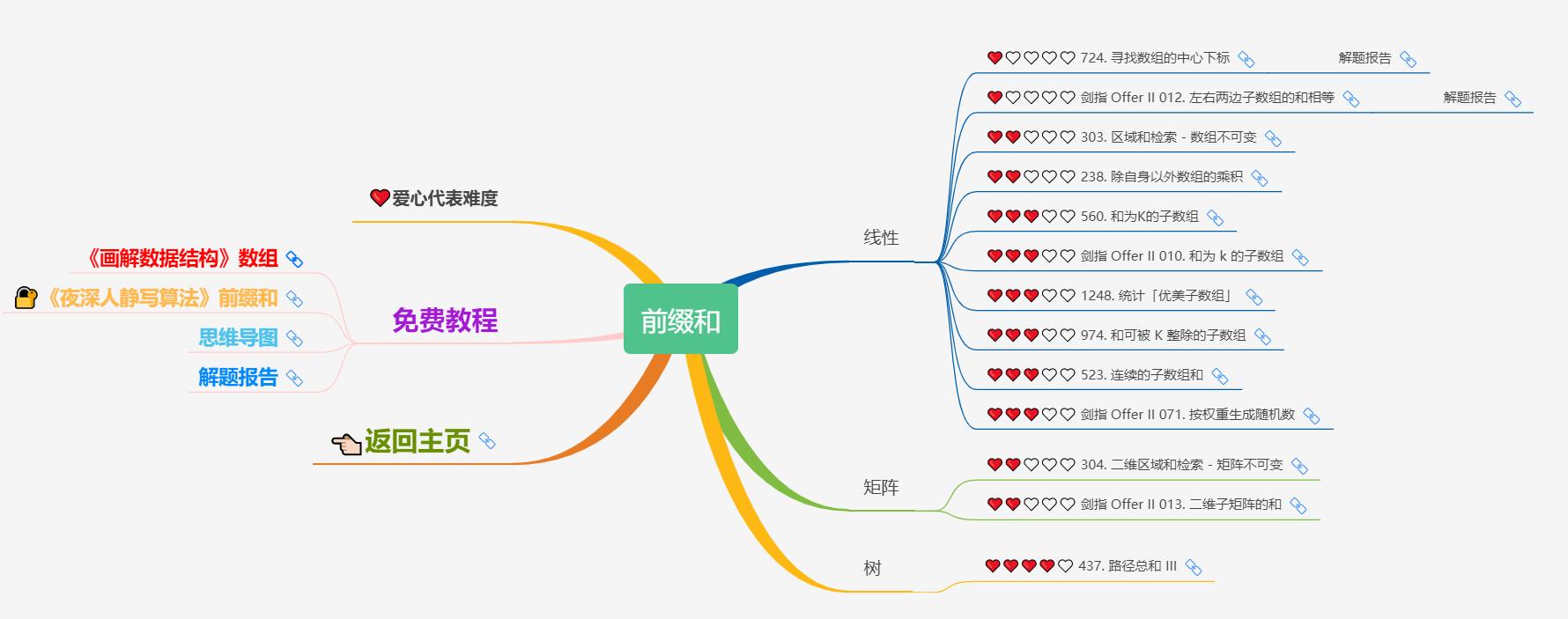
4)前缀和
5)双指针
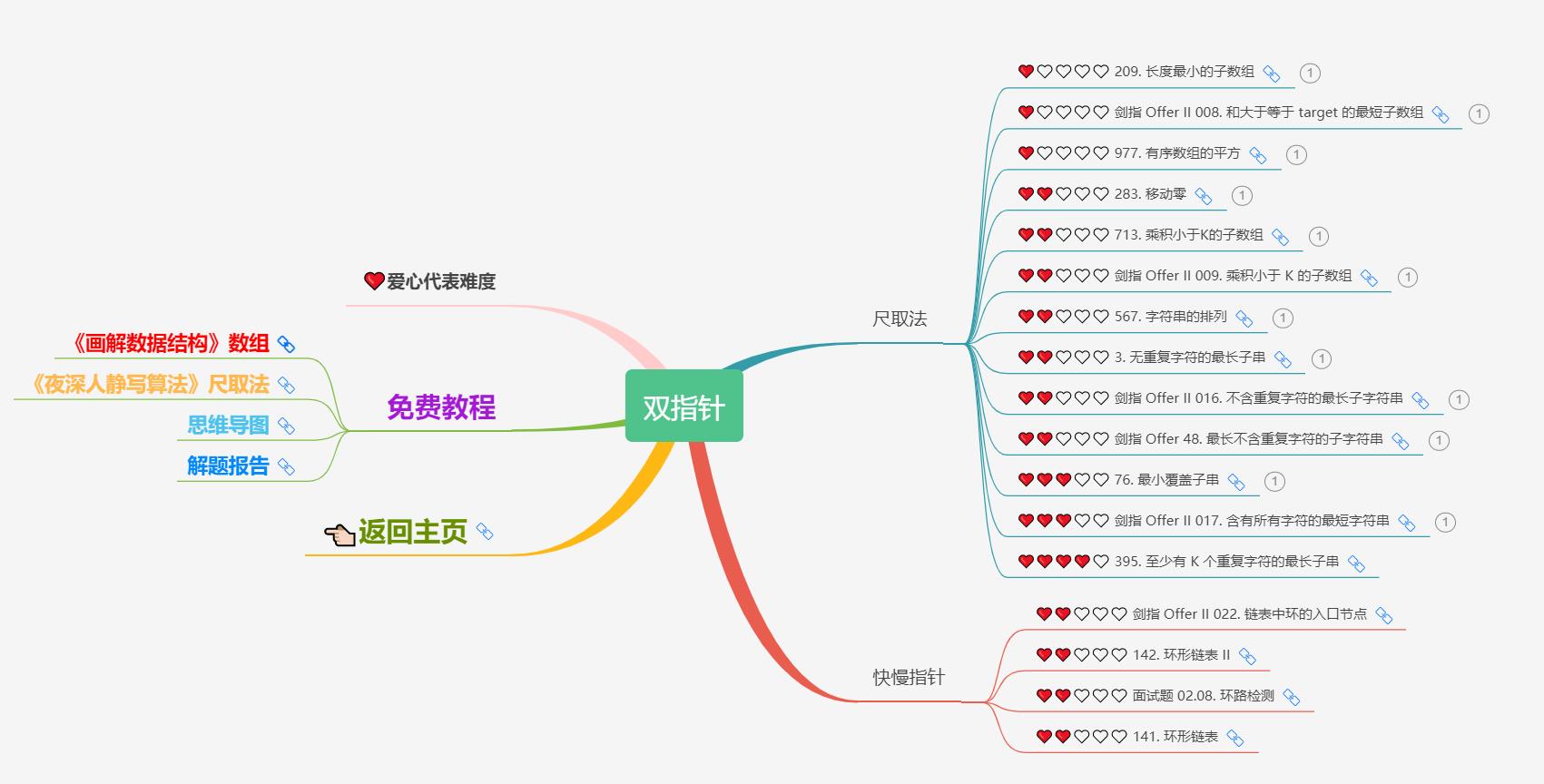
给定一个长度为 n ( 1 ≤ n ≤ 1 0 7 ) n (1 \\le n \\le 10^7) n(1≤n≤107) 的字符串 s s s,求一个最长的满足所有字符不重复的子串的长度。
样例输入:" a b c a b c b b g abcabcbbg abcabcbbg"
样例输出: 3 3 3
原题出处: LeetCode 3. 无重复字符的最长子串
我们考虑一个子串以
s
i
s_i
si 为左端点,
s
j
s_j
sj 为右端点,且
s
[
i
:
j
−
1
]
s[i:j-1]
s[i:j−1] 中不存在重复字符,
s
[
i
:
j
]
s[i:j]
s[i:j] 中存在重复字符(换言之,
s
j
s_j
sj 和
s
[
i
:
j
−
1
]
s[i:j-1]
s[i:j−1 以上是关于初步认识零基础算法的主要内容,如果未能解决你的问题,请参考以下文章