二叉树中的查找操作(按值查找按位查找)
Posted 薛定谔的猫ovo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树中的查找操作(按值查找按位查找)相关的知识,希望对你有一定的参考价值。
按值查找
查找元素值为x的结点并删除以其为根的子树
题目描述:
已知二叉树以二叉链表存储,请编写一个算法:对于树中每个元素值为x的结点,删去以它为根的子树,并释放相应的空间。
算法思想:
删除以元素值x为根的子树,只要能删除其左右子树,就可以释放值为x的结点,故采用后序的方式实现。
删除值为x的结点,意味着应将其父结点的左(右)子女指针置空,用层次遍历易于找到某结点的父结点。
要求删除树中每个元素值为x的结点的子树,故要遍历完二叉树的所有结点。
实现代码:
void DeleteXTree(BNode *bt){ //删除以bt为根的子树
if(bt != NULL){
DeleteXTree(bt->lchild);
DeleteXTree(bt->rchild);
free(bt);
}
}
//在二叉树上所有以x为元素值的结点,并删除以其为根的子树
void SearchX(BNode *root, char x){
queue<BNode *> treenode; //存放二叉树结点指针
if(root != NULL){
if(root->data == x){ //若根结点值为x,则删除整棵树
DeleteXTree(root);
}
treenode.push(root); //根结点入队
while(!treenode.empty()){
BNode *p = treenode.front();
treenode.pop(); //队首元素出队
if(p->lchild != NULL){ //若左子树非空
if(p->lchild->data == x){
DeleteXTree(p->lchild);
p->lchild = NULL; //父结点的左子女置空
}else{
treenode.push(p->lchild); //左子树的根结点入队
}
}//if
if(p->rchild != NULL){
if(p->rchild->data == x){
DeleteXTree(p->rchild);
p->rchild = NULL;
}else{
treenode.push(p->rchild);
}
}//if
}//while
}
}
在这里给出完整代码,建树使用扩展二叉树的遍历序列,为了验证删除结点后的二叉树,在执行完删除操作后,对删除后的二叉树进行层序遍历。
#include<bits/stdc++.h>
using namespace std;
typedef struct BNode{
char data;
struct BNode *lchild;
struct BNode *rchild;
}BNode;
//扩展二叉树的先序遍历序列
void BuildTree_Pre(BNode * & root, char pre[], int & i){
if(pre[i] == '#'){ //外结点,即空结点
i++;
root = NULL;
}else{
root = (BNode *)malloc(sizeof(BNode)); //建立根结点
root->data = pre[i];
i++;
BuildTree_Pre(root->lchild, pre, i); //递归建立左子树
BuildTree_Pre(root->rchild, pre, i); //递归建立右子树
}
}
void DeleteXTree(BNode *bt){ //删除以bt为根的子树
if(bt != NULL){
DeleteXTree(bt->lchild);
DeleteXTree(bt->rchild);
free(bt);
}
}
//在二叉树上所有以x为元素值的结点,并删除以其为根的子树
void SearchX(BNode *root, char x){
queue<BNode *> treenode; //存放二叉树结点指针
if(root != NULL){
if(root->data == x){ //若根结点值为x,则删除整棵树
DeleteXTree(root);
}
treenode.push(root); //根结点入队
while(!treenode.empty()){
BNode *p = treenode.front();
treenode.pop(); //队首元素出队
if(p->lchild != NULL){ //若左子树非空
if(p->lchild->data == x){
DeleteXTree(p->lchild);
p->lchild = NULL; //父结点的左子女置空
}else{
treenode.push(p->lchild); //左子树的根结点入队
}
}//if
if(p->rchild != NULL){
if(p->rchild->data == x){
DeleteXTree(p->rchild);
p->rchild = NULL;
}else{
treenode.push(p->rchild);
}
}//if
}//while
}
}
void LevelOrder(BNode *root){
queue<BNode *> treenode; //队列存储结点
if(root != NULL)
treenode.push(root); //根结点入队
while(!treenode.empty()){
BNode *p = treenode.front();
treenode.pop(); //根结点出队
printf("%c ",p->data); //输出队首元素,即当前访问的结点值
if(p->lchild != NULL){
treenode.push(p->lchild);//如果有左子树,则将左子树的根结点入队
}
if(p->rchild != NULL){
treenode.push(p->rchild);//如果有右子树,则将右子树的根结点入队
}
}
}
int main(){
BNode *root;
char pre[100];
scanf("%s",pre);
int i=0;
BuildTree_Pre(root, pre, i);
SearchX(root, 'E');
LevelOrder(root);
return 0;
}
使用的二叉树:
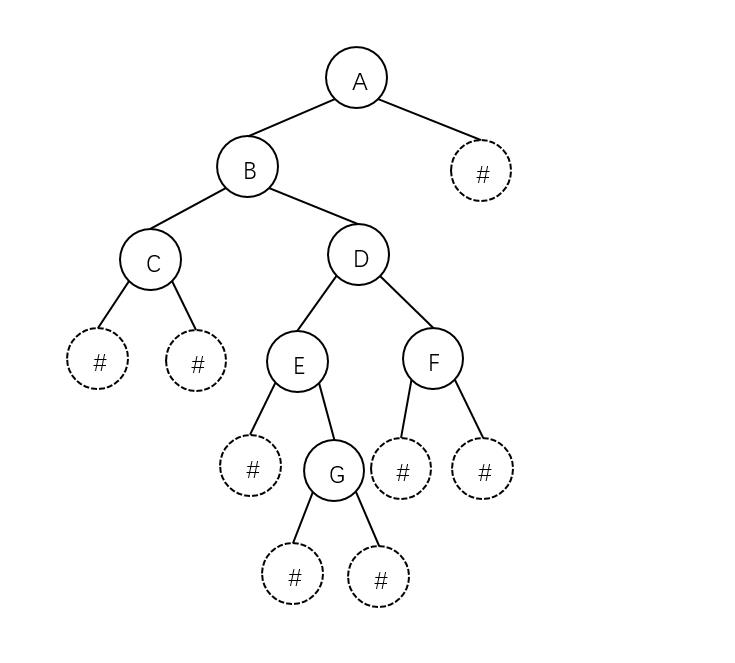
执行结果:
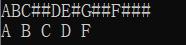
查找值为x的结点并打印其所有祖先
题目描述:
在二叉树中查找值为x的结点,试编写算法打印值为x的结点的所有祖先,假设值为x的结点不多于一个。
算法思想:
采用非递归的后序遍历,最后访问根结点,访问到值为x的结点时,栈中所有元素均为该结点的祖先,依次出栈打印即可。关于后序遍历的非递归算法,请参照详解二叉树的遍历问题(前序、后序、中序、层序遍历的递归算法及非递归算法及其详细图示)
实现代码:
void Search(BTree root, char x){
BNode *p = root;
BNode *top, *last;
stack<BNode *> treenode;
while(p || !treenode.empty()){
if(p != NULL){ //找到最左边的结点
treenode.push(p);
p = p->lchild;
}else{
top = treenode.top();
if(top->data == x){
printPath(treenode);
return;
}else{
if(top->rchild == NULL || top->rchild == last){ //右子树为空或已经访问过
treenode.pop();
// cout<<top->data<<" ";
last = top;
p = NULL;
}else{
p = top->rchild;
treenode.push(p);
p = p->lchild;
}
}
}
}
}
运行结果:
依旧使用第一个题的二叉树,查找结点G的所有祖先:

按位查找
求先序遍历序列中第k个结点的值
题目描述:
设二叉树采用二叉链表存储,设计一个算法,利用二叉树的先序遍历求先序遍历序列的第k(1 ≤ k ≤ 二叉树结点个数)个结点。
算法思想:
在先序遍历算法中加入计数器count,在访问结点的同时统计访问的序号。需要注意的是,算法中不要直接引用全局变量count,而应通过参数表显式传递count,这样能实现算法的复用。
实现代码:
BNode *PreSearchX(BTree root, int k, int &count){
if(root != NULL){
if(count == k) return root;
count++;
BNode *p = PreSearchX(root->lchild, k, count); //到左子树查找
if(p!=NULL) return p;
else return PreSearchX(root->rchild, k, count); //否则到右子树查找
}else{
return NULL;
}
}
运行结果:
依旧使用第一个题的二叉树,查找先序遍历序列中第四个结点值。
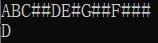
求中序遍历序列中第k个结点的值
题目描述:
设二叉树采用二叉链表存储,设计一个算法,利用二叉树的中序遍历求中序遍历序列的第k(1 ≤ k ≤ 二叉树结点个数)个结点。
算法思想:
在中序遍历算法中加入计数器count,在访问结点的同时统计访问的序号。需要注意的是,算法中不要直接引用全局变量count,而应通过参数表显式传递count,这样能实现算法的复用。
实现代码:
BNode *InSearchX(BTree root, int k, int &count){
if(root == NULL) return NULL;
BNode *p = InSearchX(root->lchild, k, count);
if(p != NULL) return p;
else{
if(count == k) return root;
count++;
return InSearchX(root->rchild, k, count);
}
}
运行结果:
依旧使用第一个题的二叉树,查找中序遍历序列中第四个结点值。
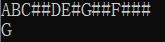
求后序遍历序列中第k个结点的值
题目描述:
设二叉树采用二叉链表存储,设计一个算法,利用二叉树的后序遍历求后序遍历序列的第k(1 ≤ k ≤ 二叉树结点个数)个结点。
算法思想:
在后序遍历算法中加入计数器count,在访问结点的同时统计访问的序号。需要注意的是,算法中不要直接引用全局变量count,而应通过参数表显式传递count,这样能实现算法的复用。
实现代码:
BNode *PostSearchX(BTree root, int k, int &count){
if(root == NULL) return NULL;
BNode *p = PostSearchX(root->lchild, k, count);
if(p != NULL) return p;
else{
p = PostSearchX(root->rchild, k, count);
if(p != NULL) return p;
if(count == k) return root;
count++;
return NULL;
}
}
运行结果:
依旧使用第一个题的二叉树,查找后序遍历序列中第四个结点值。

完整可运行代码可在我的资源中免费下载。
持续更新中。。。如有错误,欢迎指正。
以上是关于二叉树中的查找操作(按值查找按位查找)的主要内容,如果未能解决你的问题,请参考以下文章