[CF321D]Ciel and Flipboard

Posted 2021-11-07 StaroForgin

Ciel and Flipboard

题解

我们定义$s(i,j)$表示$a_{i,j}$最后取值是否是原值的相反数，容易 发现下面的性质：

• $s(i,j)\otimes s(i+m,j)\otimes s(m,j)=0(i<m)$
• $s(i,j)\otimes s(i,j+m)\otimes s(i,m)=0(j<m)$

很明显，我们每次进行操作时，是必定覆盖第$m$列的，我们的长度是超过整个正方形半的，肯定可以覆盖到中点。
如果覆盖了点$(i,m)$，那就意味着我们在第$i$肯定覆盖了连续的$m$个点，而总长度有只有$2m-1$，所以$(i,j+m)$与$(i,j)$中肯定有且仅有一个被覆盖到。
所以我们肯定会对其中两个量进行操作，所以其异或值一定是$0$的。
同理，列的部分也是一样的。

有了上面的性质，我们可以考虑将原方阵按中轴线分成四块，大概像这样：

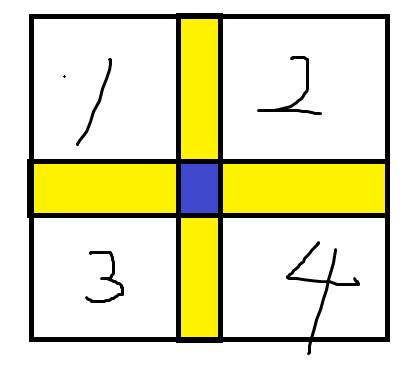
其中$1$，$2$，$3$，$4$块都是$\frac{n-1}{2}$大小的正方形，对应位置的$s$是对应相等或相反的，其相等或相反是可以根据轴上的点的奇偶性确定的。
对于一条长度为$n$的轴，我们只需要枚举前$m$个点，就可以确定这条轴上所有点的值。
而当一条轴确定后，另一条轴上所有点的值都是独立的。
我们可以枚举先枚举一条轴上前$m$个点的值，再确定另一条轴上的点取$0$还是取$1$更大。
另一条轴上的点取$0$还是取$1$更大，显然就要根据它们取$0$时所能贡献的最大值和取$1$时所能贡献的最大值比较得出，我们可以分别枚举它的两种取值，看哪个更大。
当我们两条轴的取值确定时，同一个块内不同点之间的取值都是独立的了，而不同块的对应点之间的关系也是确定的，我们只需要枚举一个点去$0$时四点和大还是取$1$时四点和大即可。
将这轴上点对应的一行或一列上的所有点的和求出来，比较大小即可。
但最开始还是要枚举半条轴的，不过时间复杂度看到$n⩽33$式应该就很容易猜出来了。

总时间复杂度$O\left(2^m{n}^2\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define debug(x) cerr<<#x<<"="<<x<<'\\n'
typedef long long LL;
typedef unsigned long long uLL;     
const LL INF=0x3f3f3f3f3f3f3f3f;  
const int mo=998244353;
const int inv2=499122177;
const int jzm=2333;
const int n1=50;
const int zero=10000;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<LL,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){putchar('\\n');while(x>9){putchar((x%10)|'0');x/=10;}putchar(x|'0');}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1LL)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1LL;}return t;}
int n,m;LL ans,a[35][35];
bool rev[35];
void work(){
	LL res=0;res+=(rev[m]?-a[m][m]:a[m][m]);
	for(int i=1;i<m;i++)
		res+=(rev[i]?-a[i][m]:a[i][m]),
		res+=((rev[i]^rev[m])?-a[i+m][m]:a[i+m][m]);
	for(int i=1;i<m;i++){
		LL sum1=a[m][i]+(rev[m]?-a[m][i+m]:a[m][i+m]);
		for(int j=1;j<m;j++)
			if(rev[j]){
				if(rev[m])sum1+=Fabs(a[j][i]-a[j][i+m]+a[j+m][i]+a[j+m][i+m]);
				else sum1+=Fabs(a[j][i]-a[j][i+m]+a[j+m][i]-a[j+m][i+m]);
			}
			else{
				if(rev[m])sum1+=Fabs(a[j][i]+a[j][i+m]+a[j+m][i]-a[j+m][i+m]);
				else sum1+=Fabs(a[j][i]+a[j][i+m]+a[j+m][i]+a[j+m][i+m]);
			}
		LL sum2=-a[m][i]+(rev[m]?a[m][i+m]:-a[m][i+m]);
		for(int j=1;j<m;j++)
			if(rev[j]){
				if(rev[m])sum2+=Fabs(a[j][i]-a[j][i+m]-a[j+m][i]-a[j+m][i+m]);
				else sum2+=Fabs(a[j][i]-a[j][i+m]-a[j+m][i]+a[j+m][i+m]);
			}
			else{
				if(rev[m])sum2+=Fabs(a[j][i]+a[j][i+m]-a[j+m][i]+a[j+m][i+m]);
				else sum2+=Fabs(a[j][i]+a[j][i+m]-a[j+m][i]-a[j+m][i+m]);
			} 
		res+=max(sum1,sum2);
	}
	ans=max(ans,res);
}
void dosaka(int id){
	if(id>m){work();return ;}
	rev[id]=1;dosaka(id+1);rev[id]=0;dosaka(id+1);
}
signed main(){
	read(n);m=(n+1)/2;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			read(a[i][j]);
	dosaka(1);
	printf("%lld\\n",ans);
	return 0;
}

谢谢！！！