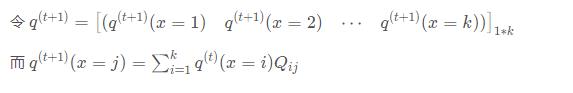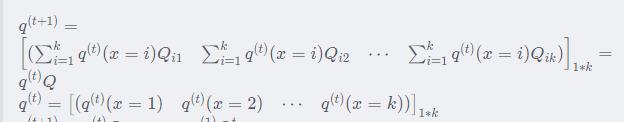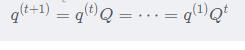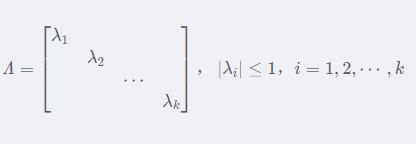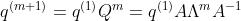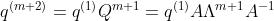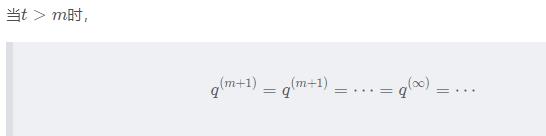MCMC笔记：齐次马尔可夫链

Posted 2021-11-07 UQI-LIUWJ

1 齐次马尔可夫链（一阶马尔可夫链）

 

1.1 马尔可夫性质

        换句话说，未来与过去无关，只和当下息息相关。 

1.2 马尔可夫链

        具有马尔可夫性的随机序列 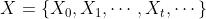称为马尔可夫链（Markov Chain），或马尔可夫过程（Markov Process）。条件概率分布P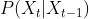称为马尔可夫链的转移概率分布。

1.3 时间齐次马尔可夫链

 2 概率转移矩阵

 （每一行的和为1）

 2.1 用概率转移矩阵说明马尔可夫链最终收敛

        可以 证明的是，经过若干步的迭代，在某一步之后，马尔可夫链最终会进入平稳分布（进入平稳状态之前，状态空间是一样的，但是各个状态的概率分布是不一样的）

 

t+1时刻状态为j的概率，等于t时刻个状态的概率*相应的转换概率，然后求和

 

所以 

         而随机矩阵，也就是状态转移矩阵，有一个性质（这里不加证明，了解就好），就是特征值的绝对值小于等于1

        所以我们对随机矩阵Q进行特征值分解的话，有：，其中特征矩阵满足：

         我们假设只有某一个λi=1，其他的λ都小于1，那么存在足够大的m，使得 （比1小的那些特征值，经过多轮乘方之后，趋近于1） 

        由于前面我们推到

        所以对m+1，我们有：

        于是，对m+2，我们有：

 这里有一个小trick'，就是因为，所以中也是有λ为1的那一个为不为0（其他位都是0乘0，或者0乘一个数），所以

所以

同样地，我们可以得到：

 也就是，在第m步之后，各个状态的状态分布是一样的，也就是马尔可夫链趋近于平稳状态

 3 状态分布

 

根据状态转移，我们有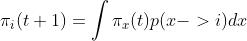： 也就是说，t+1时刻的状态i的概率，等于t时刻各个状态的概率，乘以相应的转移概率

其中所有的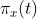的和为1

p(x-> i) ，更专业一点的写法是条件概率p(i|x)

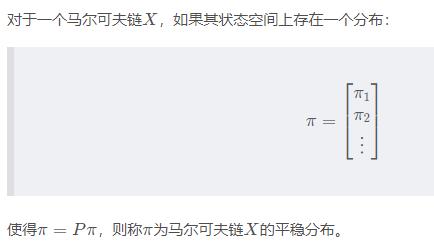
 4 平稳分布

         直观地来看，如果以该平稳分布作为初始分布，面向未来进行随机状态转移，之后任何一个时刻的状态分布都是该平稳分布。【任何时刻，各个状态的概率分布是一样的】

 上一节我们有：

而平稳分布的时候则和t没有关系了可以写成 

        而MCMC的思路，就是通过设计一个马尔可夫链，使得它可以达到平稳分布，同时平稳分布时候的概率分布Π等于我们需要的采样概率分布p(x)

4.1 detailed balance

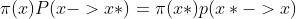
4.2 如果满足detailed balance，那么一定平稳分布

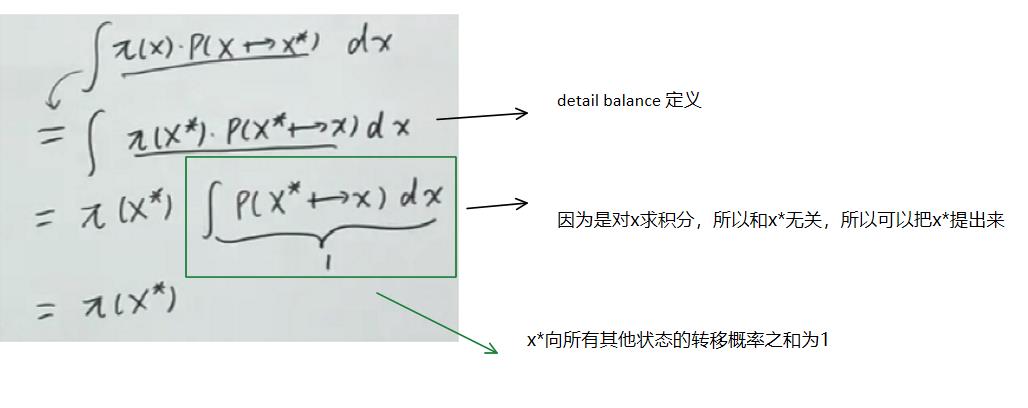
 所以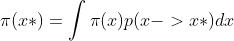，这也就是平稳分布的式子