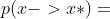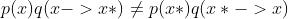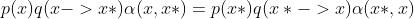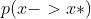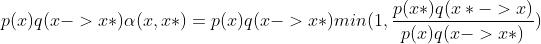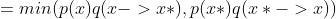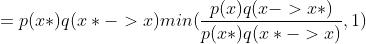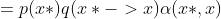MCMC笔记Metropilis-Hastings算法（MH算法）

Posted 2021-11-07 UQI-LIUWJ

1 前言

        我们在MCMC笔记：齐次马尔可夫链_UQI-LIUWJ的博客-CSDN博客 中介绍了平稳条件，当马尔可夫链达到平稳状态时（也就是各个状态之间的转移概率已经和时间无关了），那我们可以通过此时的马尔可夫链转移概率采集样本。

        比如我一开始时样本x0，那么我就根据x0到其他状态的转移概率采样，然后根据后续样

        那么现在的问题在于，什么时候达到平稳条件呢？或者说，我们怎么去找转移概率呢？

        在MCMC笔记：齐次马尔可夫链_UQI-LIUWJ的博客-CSDN博客中，我们知道detailed balance 可以推出平稳条件。

        但对于一般随机求得的转移概率q来说，

        于是我们需要构造一个系数，使得

        我们称为接受率，当等式成立的时候，就是此时平稳条件的

 2 MH算法

2.1 α（接受率）的选取

我们令

此时

                                                  

                                                 

                                                  

也即【】

所以此时满足detailed balance，所以此时的马尔可夫链满足平稳状态                           

2.2 MH算法流程

Q是我们设计出来的概率分布，我们的目的是希望Q(x)趋近于P(x)

 

 接受率是α(x,x*)

参考内容

机器学习-白板推导系列(十三)-MCMC（Markov Chain Monte Carlo）笔记 - 知乎 (zhihu.com)

机器学习-白板推导系列(十三)-MCMC（Markov Chain Monte Carlo）_哔哩哔哩_bilibili