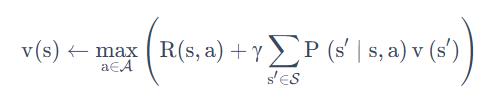MDP 笔记：Value Iteration

Posted 2021-11-07 UQI-LIUWJ

  Value Iteration 介绍

      在强化学习笔记： MDP - Policy iteration_UQI-LIUWJ的博客-CSDN博客中，我们知道，当整个状态收敛的时候，也就是已经达到最佳policy的时候，MDP会满足bellman optimality equation

        Value iteration 就是把 Bellman Optimality Equation 当成一个 update rule 来进行，如下式所示：

         

         之前我们说上面这个等式只有当整个 MDP 已经到达最佳的状态时才满足。

        但这里我们不停地去迭代 Bellman Optimality Equation，到了最后，它能逐渐趋向于最佳的策略，这是 value iteration 算法的精髓。

        

         这个算法开始的时候，它是先把所有值初始化，通过每一个状态，然后它会进行这个迭代。

        把等式 (22) 插到等式 (23) 里面，就是 Bellman optimality backup 的那个等式。

        有了等式 (22) 和等式 (23) 过后，然后进行不停地迭代，迭代过后，然后收敛，收敛后就会得到这个v∗

        当我们有了v∗ 过后，一个问题是如何进一步推算出它的最佳策略。

        提取最佳策略的话，我们可以直接用 arg max。就先把它的 Q 函数重构出来，重构出来过后，每一个列对应的最大的那个 action 就是它现在的最佳策略。这样就可以从最佳价值函数里面提取出最佳策略。

 2 对比 policy iteration 和 value iteration

这两个算法都可以解 MDP 的控制问题。

• Policy Iteration 分两步，首先进行 policy evaluation，即对当前已经搜索到的策略函数进行一个估值。得到估值过后，进行 policy improvement，即把 Q 函数算出来，我们进一步进行改进，选取Q最大的策略。不断重复这两步，直到策略收敛。
• Value iteration 直接把 Bellman Optimality Equation 拿进来，然后去寻找最佳的 value function，没有 policy function 在这里面。当算出 optimal value function 过后，我们再来提取最佳策略。（所以我策略在迭代的过程中是不变的）

• 在Policy Iteration中
  • 第一步 Policy Eval：一直迭代至收敛，获得准确的V(s)
  • 第二步 Policy Improvement：根据准确的V(s)，求解最好的Action
• 对比之下，在Value Iteration中
  • 第一步 "Policy Eval"：迭代只做一步，获得不太准确的V(s)
  • 第二步 "Policy Improvement"：根据不太准确的V(s)，求解最好的Action