P1450 [HAOI2008]硬币购物

Posted 2021-11-07 Jozky86

P1450 [HAOI2008]硬币购物

题意：

共有 4 种硬币。面值分别为$c_1,c_2,c_3,c_4$。
某人去商店买东西，去了 n 次，对于每次购买，他带了 $d_i$枚 i 种硬币，想购买 s 的价值的东西。请问每次有多少种付款方法。

题解：

第一感觉是母函数，但写不出来，后来看题解时确实可以做，NTT+多项式求逆+母函数，麻烦而且跑的很慢，不过洛谷可以过，这里不做详细讲解，可以看看代码
母函数做法的代码
我们这里讲下完全背包+容斥的做法
如果题目没有数量的限制，可以完全背包做法
现在有了数量限制，我们可以用差分来求，举个例子：
$[2,+\infty )-(3,+\infty )=[2,+\infty )-[4,+\infty )=[2,3]$,显然只要我们求出$[2,+\infty )$和$(3,+\infty )$，就可以算出[2,3]。可以认为$[x,+\infty )$表示价值大于等于x的方案数，可以用完全背包去求。
现在我们用完全背包先预处理出没有钱数限制的所有情况，然后减去不合法情况(即某种硬币超出了所给数量)，得到的不就是答案：
$ans=f[s]-{\sum }_{i=1}^{4}f[s-c_i\ast (d_i+1)]$
现在的任务就是求${\sum }_{i=1}^{4}f[s-c_i\ast (d_i+1)]$,可能会认为直接累加不就可以了，并不是，因为i=1，2，3，4，这四部分并不是完全独立的，换句话说，有可能第一种物品超出限制的同时，第二种也超出了，如果直接累加必然会造成重复计算。这咋整？这个模型很想中学学过的容斥原理：
这个式子应该很熟悉：
三元容斥：

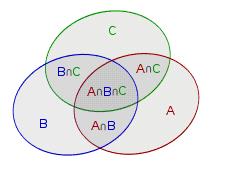
A∪B∪C=(A∪B)∪C=A+B+C−A∩B−A∩C−B∩C+A∩B∩C
扩展一下：
奇加偶减

我们设四种硬币分别是A，B，C，D，card(X)表示X集合元素个数
答案=$f[s]=card(A\bigcup B\bigcup C\bigcup D)$
$=f[s]-ans$
$ans=card(A)+card(B)+card(C)+card(D)-card(A\bigcap B)-card(A\bigcap C)-card(A\bigcap D)-card(B\bigcap C)-card(B\bigcap D)-card(C\bigcap D)+card(A\bigcap B\bigcap C)+card(A\bigcap B\bigcap D)+card(B\bigcap C\bigcap D)-card(A\bigcap B\bigcap C\bigcap D)$
我们刚才说了奇加偶减，所以二进制枚举(第i位为0表示这个card()种并没有因为i，否则有)，直接从0(0000)枚举到15(1111)就可以。
本题难点还是在于将完全背包与容斥结合，两个分开看都不算难

代码：

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
    x= 0;
    char c= getchar();
    bool flag= 0;
    while (c < '0' || c > '9')
        flag|= (c == '-'), c= getchar();
    while (c >= '0' && c <= '9')
        x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
    if (flag)
        x= -x;
    read(Ar...);
}
template <typename T> inline void write(T x)
{
    if (x < 0) {
        x= ~(x - 1);
        putchar('-');
    }
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#else
    startTime = clock ();
    freopen("data.in", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#else
    endTime= clock();
    printf("\\nRun Time:%lfs\\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn=1e5+9;
ll ans,f[maxn]; 
int c[5];//面值 
int d[5];//数量 
void pre(){
	f[0]=1;
	for(int i=1;i<=4;i++){
		for(int j=c[i];j<=100001;j++){
			f[j]+=f[j-c[i]];
		}
	}
}
int s;
void cal(){
	ans=0;
	for(int i=1;i<=(1<<4)-1;i++){
		ll k=0,num=0;
		for(int j=0;j<4;j++){
			if(i&(1<<j))//第j位是1
			{
				num++;
				k+=c[j+1]*(d[j+1]+1); 
			} 
		}
		ll flag=1;
		if(num%2==0)flag=-1*flag;
		if(s>=k)ans+=flag*f[s-k];
	}
	ans=f[s]-ans;
}
int main()
{
    //rd_test();
	for(int i=1;i<=4;i++)cin>>c[i];
	pre();
	int t;
	read(t);
	while(t--){
		ans=0;
		for(int i=1;i<=4;i++)cin>>d[i];
		
		cin>>s;
		cal();
		cout<<ans<<endl;
	}
    //Time_test();
}