《LeetCode之每日一题》:181.数字的补数

Posted 2021-11-07 是七喜呀！

数字的补数

• 有关题目
• • 题解

题目链接： 数字的补数

有关题目

对整数的二进制表示取反（0 变 1 ，1 变 0）后，再转换为十进制表示，可以得到这个整数的补数。

例如，整数 5 的二进制表示是 "101" ，取反后得到 "010" ，再转回十进制表示得到补数 2 。
给你一个整数 num ，输出它的补数。

示例 1：

输入：num = 5
输出：2
解释：5 的二进制表示为 101（没有前导零位），其补数为 010。所以你需要输出 2 。

示例 2：

输入：num = 1
输出：0
解释：1 的二进制表示为 1（没有前导零位），其补数为 0。所以你需要输出 0 。

提示：

1 <= num < 2^31

题解

法一：额外空间存储num二进制字符串

class Solution {
public:
    int findComplement(int num) {
        int ans = 0;
        string temp;
        //倒序存放num的二进制 并取反
        while(num)//101
        {
            temp.push_back((!(num % 2) + '0'));
            num /= 2;
        }
        
        //根据num的二进制位数我们可以知道，num的补树 的二进制位数
        for (int i = temp.size() - 1; i >= 0; i--)
            ans |= ((temp[i] - '0') << i);

        return ans;

    }
};

时间复杂度：O(k)，找出num 的二进制最高位1所需的次数
空间复杂度：O(k),存放num 的二进制序列

法二：位运算
代码一：
参考题解数字的补数（巧解）

输入为 5 是 101
输出为 2 是 010
上下两个加起来就是 111 即2的3次方-1

输入为 8 是 1000
输出为 7 是 0111
上下两个加起来就是 1111 即2的4次方-1

同理
就可以知道
找到一个比num大的 2的n次幂的数 本题为a
然后结果就是a - num - 1

class Solution {
public:
    int findComplement(int num) {
        long a = 1;

        while(true)
        {
            if (num >= a)
                a *= 2;
            else 
                return a - 1 - num;
        }
    }
};

代码二：
参考官方题解

class Solution {
public:
    int findComplement(int num) {
        int highbit = 0;
        for (int i = 1; i <= 30; i++)
        {
            if (num >= (1 << i))
                highbit = i;
            else 
                break;
        }

        int mask = (highbit == 30 ? 0x7fffffff : (1 << (highbit + 1)) - 1);
        return num ^ mask;
    }
};

法三：遍历找最高位1

class Solution {
public:
    int findComplement(int num) {
        int s = -1;
        for (int i = 31; i >= 0; i--)
        {
            if (((num >> i) & 1) != 0)//拿到最高位的1
            {
                s = i;
                break;
            }
        }
        //代码三：遍历找最高位一
        int ans = 0;//顺序取反
        for (int i = 0; i < s; i++)
        {
            if (((num >> i) & 1) == 0)
                ans |= (1 << i);
        }

        return ans;
    }
};

法四：lowbit
参考宫水三叶

假设我们找到最高位1所表示的值s，那么最终结果为，num 取反
按位与上s - 1

class Solution {
public:
    int findComplement(int num) {
        int s = -1;
        for (int i = num; i != 0; i -= (i & -i))
            s = i;
        
        return ~num & (s - 1);

    }
};

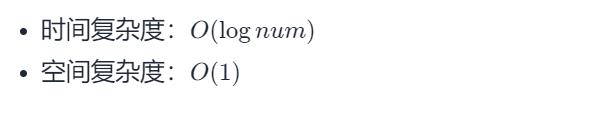
法五：利用无符号数，前缀加一
参考官方题解评论区下wangYiTiaoYu🐟

class Solution {
public:
    int findComplement(int num) {
        uint t = 1u << 31;
        while(! (t & num))
        {
            num |= t;
            t >>= 1;
        }

        return ~num;
    }
};