BSV 上的图灵机
Posted freedomhero
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BSV 上的图灵机相关的知识,希望对你有一定的参考价值。
我们通过实践证明任何图灵机都可以在 Bitcoin 上进行模拟,从而证明它是图灵完备的¹。我们已经实现了一个识别平衡括号的图灵机,并将其部署在 BSV 区块链上。任何其他的图灵机都可以用同样的方式模拟。
图灵机简介
图灵机由以下组件(简化)组成:
-
当前状态,在一组有限的状态中(一个状态标记为初始状态,一些状态标记为结束状态)
-
带有存储单元和可以在磁带上移动的读/写头的磁带
-
一个所谓的转换函数,它告诉机器该做什么和什么时候做。
在下面的示例中,我们展示了用于检查平衡括号的图灵机。它的初始状态是 A 并且它包含一个接受状态。转换函数表示,例如,如果图灵机处于状态 A 并且其头部读取符号“(”,则它应该在该单元格中写入“X”并向左移动,转换到状态 B。
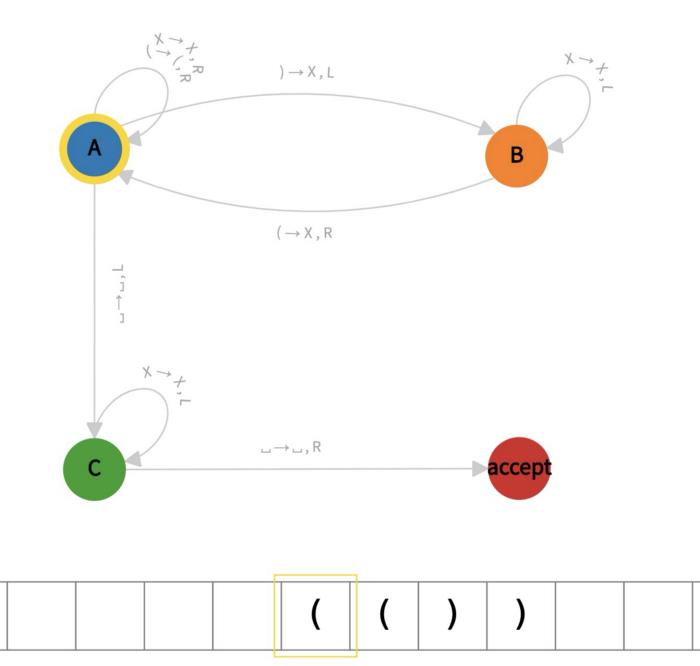
邱奇-图灵论题
邱奇-图灵 论题指出,图灵机可以计算任何可以计算的东西。它是计算的定义,也是计算机理论的基本工具。
在 BSV 上模拟图灵机
我们将展示一种在 BSV 上模拟图灵机的通用方法。我们获取正在运行的图灵机的快照:磁头位置、当前状态和磁带。快照存储在有状态的 BSV 智能合约中。更具体地说,它们是 BSV 交易的输出。运行图灵机的每一步都由 BSV 交易触发。图灵机可以继续运行,除非它进入可接受的状态。
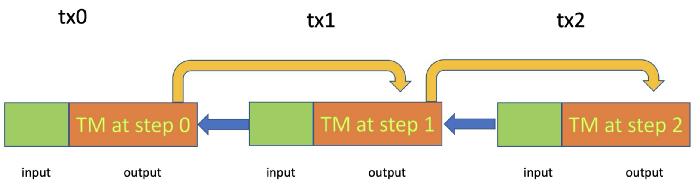
实现
为了证明在 BSV 上模拟图灵机的可行性,我们已经实现了前面提到的图灵机来检查平衡括号,如下所示。
contract TuringMachine {
// states
static const State STATE_A = b'00'; // initial state
static const State STATE_B = b'01';
static const State STATE_C = b'02';
static const State STATE_ACCEPT = b'03';
// symbols
static const Symbol BLANK = b'00';
static const Symbol OPEN = b'01';
static const Symbol CLOSE = b'02';
static const Symbol X = b'03';
static const bool LEFT = true;
static const bool RIGHT = false;
// number of rules in the transition function
static const int N = 8;
// transition function table
static const TransitionFuncEntry[N] transitionFuncTable = [
{{STATE_A, OPEN}, {STATE_A, OPEN, RIGHT}},
{{STATE_A, X}, {STATE_A, X, RIGHT}},
{{STATE_A, CLOSE}, {STATE_B, X, LEFT}},
{{STATE_A, BLANK}, {STATE_C, BLANK, LEFT}},
{{STATE_B, OPEN}, {STATE_A, X, RIGHT}},
{{STATE_B, X}, {STATE_B, X, LEFT}},
{{STATE_C, X}, {STATE_C, X, LEFT}},
{{STATE_C, BLANK}, {STATE_ACCEPT, BLANK, RIGHT}}
];
public function transit(SigHashPreimage txPreimage, int amount) {
// read/deserialize contract state
// ...
// transition
Symbol head = Util.getElemAt(s.tape, s.headPos);
// look up in transition table
bool found = false;
loop (N) : i {
if (!found) {
auto entry = transitionFuncTable[i];
if (entry.input == {s.curState, head}) {
auto output = entry.output;
// update state
s.curState = output.newState;
// write tape head
s.tape = Util.setElemAt(s.tape, s.headPos, output.write);
// move head
s.headPos += output.moveLeft ? -1 : 1;
// extend tape if out of bound
if (s.headPos < 0) {
// add 1 blank cell to the left
s.tape = BLANK + s.tape;
s.headPos = 0;
} else if (s.headPos >= len(s.tape)) {
// add 1 blank cell to the right
s.tape = s.tape + BLANK;
}
if (s.curState == STATE_ACCEPT) {
// accept
exit(true);
}
found = true;
}
}
}
// reject if no transition rule found
require(found);
// otherwise machine goes to the next step
// write/serialize contract state
// ...
}
}
每次在Tx中调用公共函数transit() 时,机器前进一步。
- Line3-6:定义状态,包括初始状态和接受状态
- Line9-12:定义所有符号
- Line19-30:将转换函数定义为表格
- Line37:从头部读取符号
- Line40-43:使用当前状态和磁头符号,我们在转移函数表中查找新状态(L46),写入磁带(L48),移动磁头(L50)。
- Line51-59:最初磁带只包含输入字符串,例如“(())()()”。如果任何时候磁带用完,无论是在左侧 (L52) 还是右侧 (L56),都会添加一个空白单元格。这确保磁带可以任意长并且是无界的(但不是无限²)。
部署
我们已经将上面的图灵机部署到 BSV ,并在输入字符串“(())()()”上运行它。完整的执行如下所示。
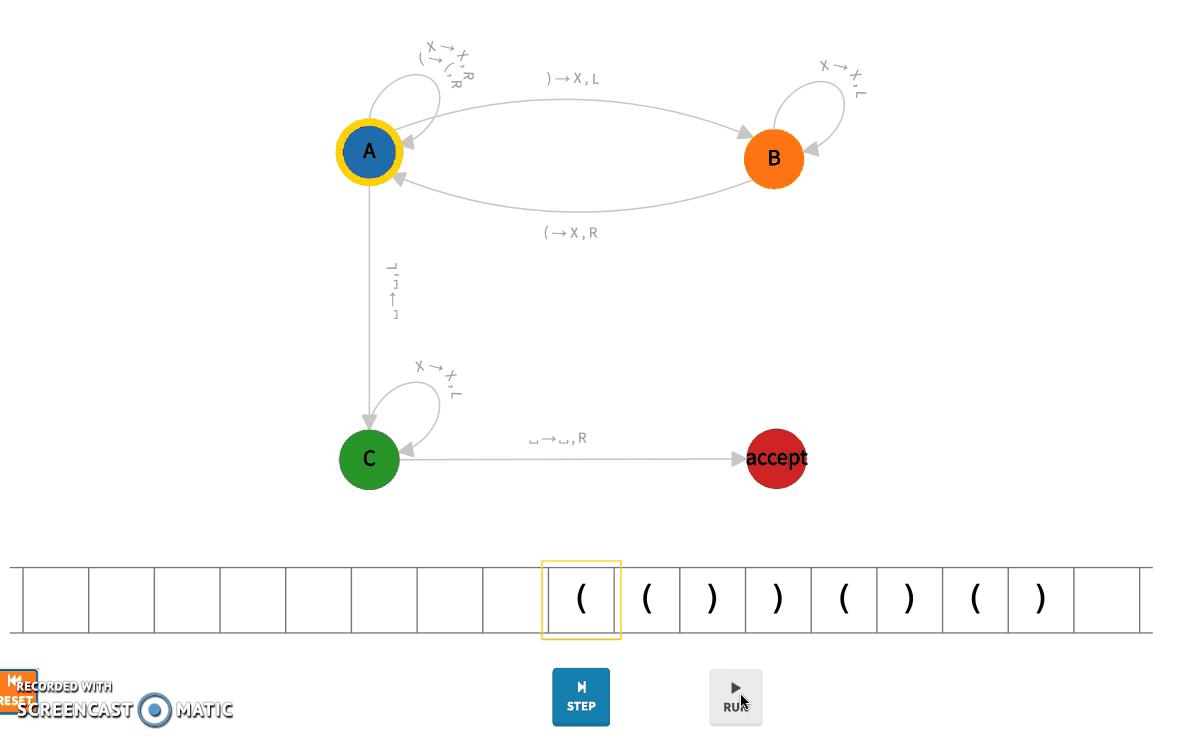
这是第 0 步的图灵机:
你可以看到图灵机的快照被编码在这个交易中。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Oj8CR4DR-1634546788844)(./1__YgTJBZ-3YtWG92I8XAPfA.png)]
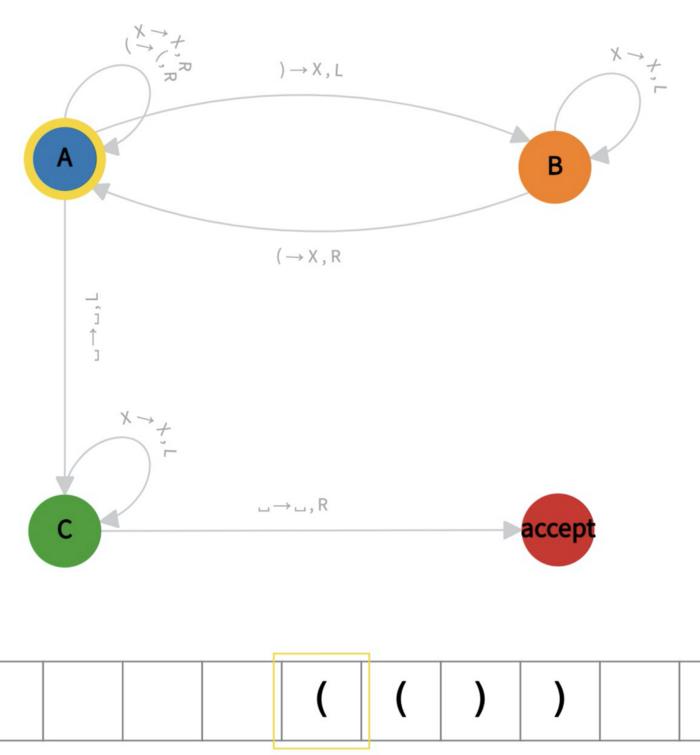
同样,这是第 3 步:
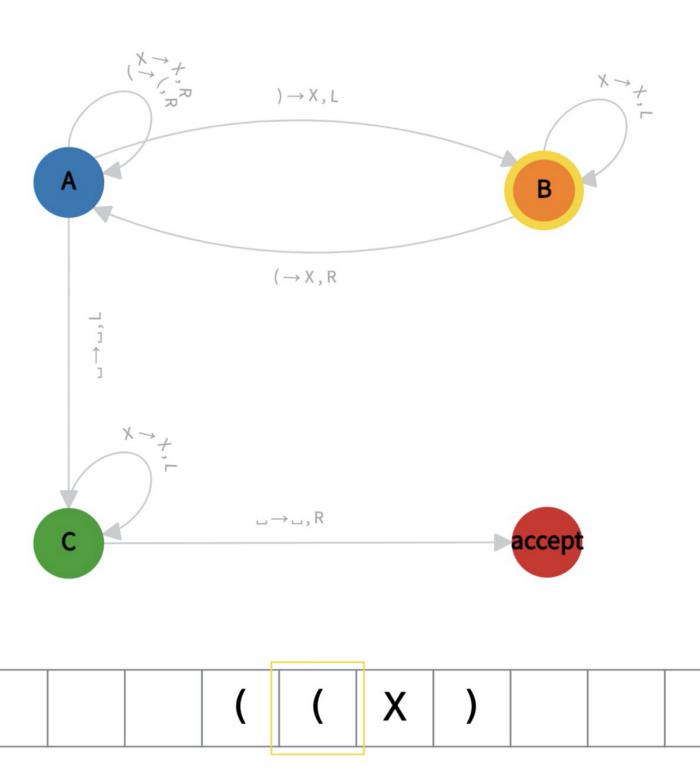
它的编码如下:
图灵完备证明
通过简单地更改状态、符号和转换函数,可以很简单地将上述图灵机合约改编为实现任何其他图灵机。因此,任何图灵机都可以在 BSV 上进行模拟,最终证明 BSV 根据定义是图灵完备的。 QED。
在可计算性理论中,如果一个数据操作规则系统可用于模拟任何图灵机,则称其为图灵完备的
致谢
感谢 Pasquale Valentin 帮助在 BSV 上部署合约。
[1] 我们通过在 BSV 上实施图灵竞争系统(例如康威的生命游戏和规则 110),展示了 BSV 是图灵完备的。
[2] 无限与无界 作者:Craig Wright | 2021 年 9 月 14 日
以上是关于BSV 上的图灵机的主要内容,如果未能解决你的问题,请参考以下文章