简单滤波算法常见的滤波算法讲解及例程

Posted 2021-11-06 Z小旋

• • 限幅滤波法
  • • 算法：
    • 优点：
    • 缺点
    • 代码：
  • 中位值滤波法
  • • 算法：
    • 优点：
    • 缺点：
    • 代码：
  • 算术平均值滤波
  • • 算法：
    • 优点：
    • 缺点：
    • 代码：
  • 滑动算术平均值滤波
  • • 算法：
    • 优点：
    • 缺点：
  • 中位值平均滤波法
  • • 算法：
    • 优点：
    • 缺点：
    • 代码
  • 一阶低通滤波
  • • 方法：
    • 优点：
    • 缺点：
    • 代码：

限幅滤波法

算法：

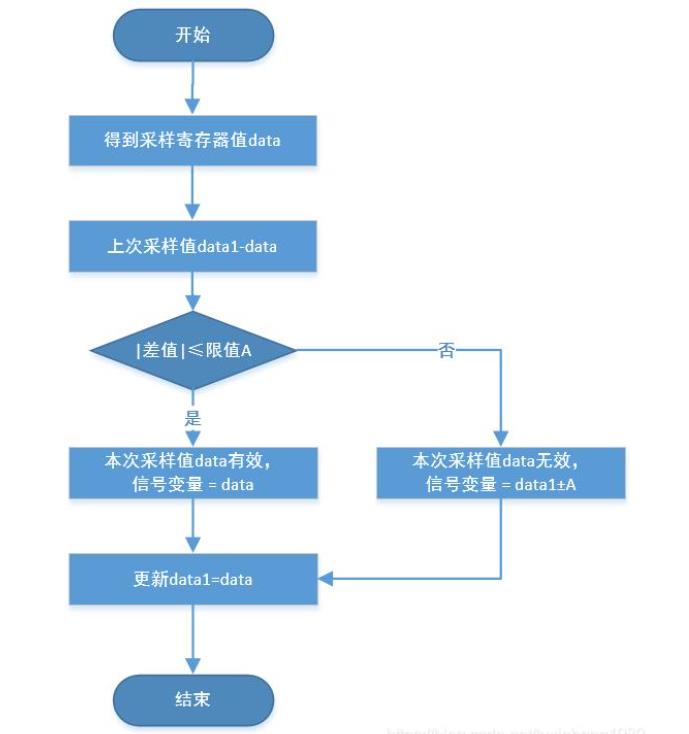
确定两次采样允许的最大偏差值（设为 A）
每次检测到新的采样值时判断：
如果本次值与上次值之差<=A,则本次采样值有效
如果本次值与上次值之差>A,则本次采样值无效。

如果本次采样值无效，对本次采样可以做不同的处理。
比方说：

• 放弃本次采样值，使用上次采样值作为本次采样值
• 本次采样值=上次采样值± 限幅A
• 放弃本次采样值，重新采样

优点：

• 能够消除因偶然波动引起的误差

缺点

• 无法抑制周期性的干扰
• 平滑度差
  

代码：

  /* variation_Range  值可根据实际情况调整*/
    #define variation_Range 10
    
    char Bounds_Filter(char new_value,char old_value)
    {
        if( abs(new_value - old_value> variation_Range ))
            return old_value;      
       	return new_value;
   }

或：

  /* 10为限幅值，可根据实际情况调整*/

  new_value= abs(new_value - old_value) > 10 ? old_value:new_value ;//限幅  

一行代码搞定

中位值滤波法

算法：

连续采样奇数个数据，然后对数据从小到大排序，取中间的值做为本次采样值

优点：

中位值滤波法可以滤除偶然因素引起的脉冲干扰，可以滤除数据的毛刺，使采样数据更加平滑。
适用于变化缓慢的较为线性的采样系统，如温度等被测参数

缺点：

采样值快速变化的系统不宜使用

代码：

//采样samples_Num次，然后用冒泡排序进行排序，最后取中值

#define samples_Num  5  //采样次数
 
int Median_Filter()
{
    unsigned int value[M] = {0};
    unsigned int count, i, j, temp;
    for( count = 0; count < samples_Num  ; count++ )
    {
        value[count] = Read_Adc();
    }
    for( j = 0; j < samples_Num - 1; j++ )
    {
        for( i = 0; i < samples_Num - j - 1; i++ )
        {
            if( value[i] > value[i + 1] )
            {
                temp = value[i];
                value[i] = value[i + 1];
                value[i + 1] = temp;
            }
        }
    }
    return value[( M - 1 ) / 2];
}

算术平均值滤波

算法：

在某时刻对信号进行连续多次采样，对采样值进行算术平均(平均值)，作为该时刻的信号采样值

就是取平均值，连续采样的次数视具体情况而定

优点：

对抑制周期性干扰和随机干扰有良好效果

缺点：

采样比较耗时，并且平均值可能受到某个数据干扰而产生较大浮动。

代码：

#define N 10
int value = 0;
 
int Arithmetic_Filter()
{
	for(int i = 0; i < N; i++)
	{
    	    value = value + Read_Adc();
	}
        return (value/N);
}

滑动算术平均值滤波

算法：

滑动平均值滤波是指先在RAM中建立一个数据缓冲区，依顺序存放N个采样数据，每采进一个新数据，就将最早采集的那个数据丢掉，而后求包括新数据在内的N个数据的算术平均值或加权平均值。这样，每进行一次采样，就可计算出一个新的平均值，从而加快了数据处理的速度.

优点：

对周期性干扰有良好的抑制作用,平滑度高

缺点：

灵敏度低
对干扰抑制作用低

#define size 6000//数组大小
#define N 12//滑动平均滤波计算平均值时所取的点数
/*上面两句在使用下面这个函数的时候加到程序的开头*/
void Smooth(float data[])
{
    Sum1=0;
    for(int j=0;j<size;j++)
    {
        if(j<N/2)
        {
            for(int k=0;k<N;k++)
            {
                Sum1+=data[j+k];
            }
            data[j]=Sum1/N;
        }
        else
            if(j<size -N/2)
            {
                for(int k=0;k<N/2;k++)
                {
                    Sum1+=(data[j+k]+data[j-k]);
                }
                data[j]=Sum1/N;
            }
            else
            {
                for(int k=0;k<size-j;k++)
                {
                    Sum1+=data[j+k];
                }
                for(int k=0;k<(N-size+j);k++)
                {
                    Sum1+=data[j-k];
                }
                data[j]=Sum1/N;
            }
        Sum1=0;
    }
}

中位值平均滤波法

算法：

连续采样 N 个数据,去掉最大值和最小值 ，然后计算 N‐2 个数据的平均值，作为采样值

优点：

对于偶然出现的脉冲性干扰,可消除由于脉冲干扰所引起的采样值偏差

缺点：

用时比较久

代码

#define N 12

 

unsigned int Med_Avg_Filter()
{
    unsigned int count, i, j, temp;
    unsigned int value_buf[N];
    int  ad_sum= 0;
    //采样N次
    for( count = 0; count < N; count++ )
    {
        value_buf[count] =  Read_ADC();
    }
/*=========================冒泡排序升序==========================*///舍弃最大值和最小值   
    for( j = 0; j < N - 1; j++ )
    {
        for( i = 0; i < N - j - 1; i++ )
        {
            if( value_buf[i] > value_buf[i + 1] )
            {
                temp = value_buf[i];
                value_buf[i] = value_buf[i + 1];
                value_buf[i + 1] = temp;
            }
        }
    }
    //求中间项的和
    for( count = 1; count < N - 1; count++ )
    {
        ad_sum+= value_buf[count];
    }
    return (ad_sum/( N -2 ));
}
}

一阶低通滤波

方法：

滤波结果=a*本次采样值+（1-a）*上次滤波结果

a取值为0~1之间

就是将新的采样值与上次的滤波结果计算一个加权平均值。

a的取值决定了算法的灵敏度，a越大，新采集的值占的权重越大，算法越灵敏，但平顺性差；相反，a越小，新采集的值占的权重越小，灵敏度差，但平顺性好

优点：

对周期性干扰具有良好的抑制作用
适用于波动频率较高的场合

缺点：

相位滞后,灵敏度低

代码：

float final=0;
float a=0.25;  
 
float first_Order_Filter(float data)
{
	final = a*data + (1-a)*final;	
	return(final);
}