ABC222 G - 222(数论,欧拉定理)
Posted live4m
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ABC222 G - 222(数论,欧拉定理)相关的知识,希望对你有一定的参考价值。
题意:
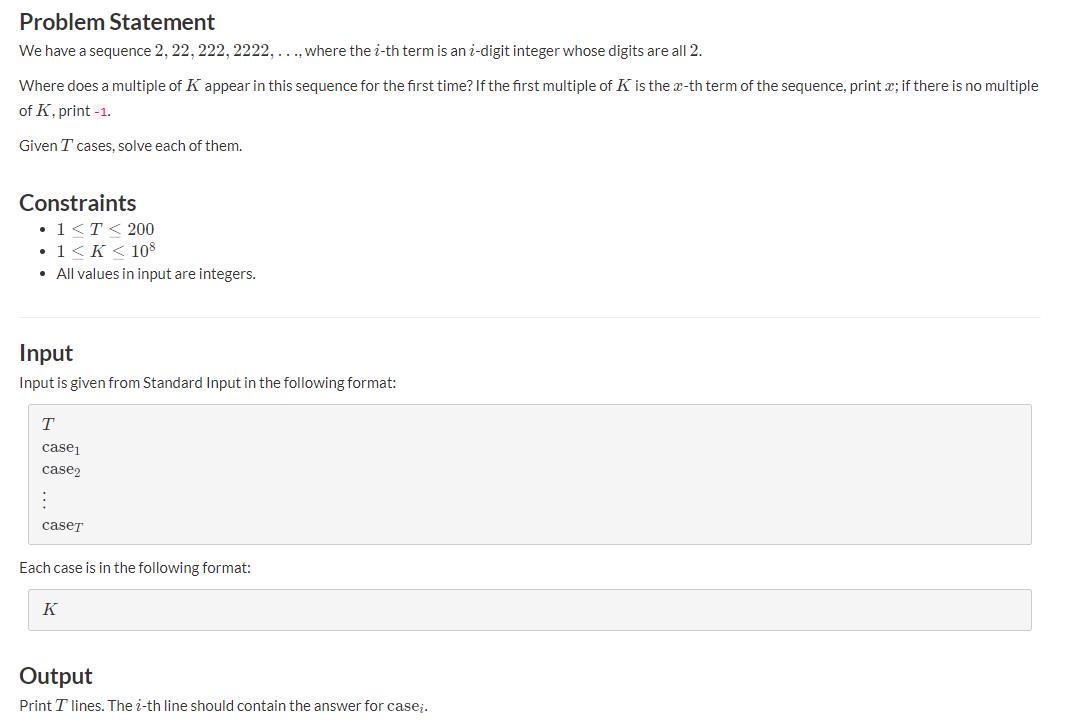
解法:
设 最 后 的 答 案 为 n 222... = 2 9 ( 1 0 n − 1 ) 2 9 ( 1 0 n − 1 ) = 0 ( m o d k ) 2 ( 1 0 n − 1 ) = 0 ( m o d 9 k ) 1 0 n − 1 = 0 ( m o d 9 k g c d ( 9 k , 2 ) ) 1 0 n = 1 ( m o d 9 k g c d ( 9 k , 2 ) ) 设 M = 9 k g c d ( 9 k , 2 ) 1 0 n = 1 ( m o d M ) 容 易 证 明 10 和 M 互 质 , 此 时 根 据 欧 拉 定 理 有 : 1 0 ϕ ( M ) = 1 ( m o d M ) n 一 定 是 ϕ ( M ) 的 因 子 O ( s q ) 枚 举 因 子 , 取 合 法 的 最 小 值 即 可 . − − − − − 待 补 : 为 什 么 n 一 定 是 ϕ ( M ) 的 因 子 ? 设最后的答案为n\\\\ 222...=\\frac{2}{9}(10^n-1)\\\\ \\frac{2}{9}(10^n-1)=0 (mod\\ k)\\\\ 2(10^n-1)=0(mod\\ 9k)\\\\ 10^n-1=0(mod\\ \\frac{9k}{gcd(9k,2)})\\\\ 10^n=1(mod\\ \\frac{9k}{gcd(9k,2)})\\\\ 设M=\\frac{9k}{gcd(9k,2)}\\\\ 10^n=1(mod\\ M)\\\\ 容易证明10和M互质,此时根据欧拉定理有:\\\\ 10^{\\phi(M)}=1(mod\\ M)\\\\ n一定是\\phi(M)的因子\\\\ O(sq)枚举因子,取合法的最小值即可.\\\\ -----\\\\ 待补:为什么n一定是\\phi(M)的因子?\\\\ 设最后的答案为n222...=92(10n−1)92(10n−1)=0(mod k)2(10n−1)=0(mod 9k)10n−1=0(mod gcd(9k,2)9k)10n=1(mod gcd(9k,2)9k)设M=gcd(9k,2)9k10n=1(mod M)容易证明10和M互质,此时根据欧拉定理有:10ϕ(M)=1(mod M)n一定是ϕ(M)的因子O(sq)枚举因子,取合法的最小值即可.−−−−−待补:为什么n一定是ϕ(M)的因子?
code:
#include<bits/stdc++.h>
#define MULTI_CASE
#define SYNC_OFF
#define PI pair<int,int>
#define ll long long
#define int long long
using namespace std;
// const int mod=998244353;
const int mod=1e9+7;
const int maxm=2e6+5;
int ppow(int a,int b,int mod){
int ans=1%mod;a%=mod;
while(b){if(b&1)ans=1ll*ans*a%mod;a=1ll*a*a%mod;b>>=1;}
return ans;
}
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
int k;
int phi(int n){
int ans=n;
for(int i=2;i*i<=n;i++){
if(n%i==0){
while(n%i==0)n/=i;
ans=ans/i*(i-1);
}
}
if(n!=1)ans=ans/n*(n-1);
return ans;
}
bool check(int n,int mod){
return ppow(10,n,mod)==1;
}
void solve(){
cin>>k;
int M=9*k/gcd(9*k,2);
int P=phi(M);
set<int>s;
for(int i=1;i*i<=P;i++){
if(P%i==0){
if(check(i,M)){
s.insert(i);
}
if(check(P/i,M)){
s.insert(P/i);
}
}
}
if(s.size())cout<<*s.begin()<<endl;
else cout<<-1<<endl;
}
void Main(){
#ifdef MULTI_CASE
int T;cin>>T;while(T--)
#endif
solve();
}
void Init(){
#ifdef SYNC_OFF
ios::sync_with_stdio(0);cin.tie(0);
#endif
#ifndef ONLINE_JUDGE
freopen("../in.txt","r",stdin);
freopen("../out.txt","w",stdout);
#endif
}
signed main(){
Init();
Main();
return 0;
}
以上是关于ABC222 G - 222(数论,欧拉定理)的主要内容,如果未能解决你的问题,请参考以下文章