D. Present按位拆分算贡献

Posted 2021-11-05 goto_1600

链接

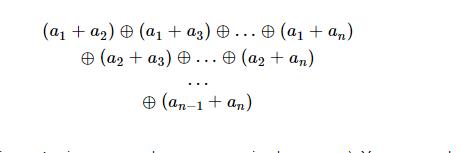
求这个公式的答案 n<=400000 ,a[i]<=4e7
思路：
一开始就想到了按位算贡献，但是没有发掘一个性质，某一位k只受<=它的位数所影响，所以我们可以考虑按位统计，出现第k位为1有两种情况，一种情况是两数之和>=(1<<k) && <(1<<(k+1)) 还有一种是>=(1<<k)+(1<<(k+1)) ，在统计每一位的时候将a[i]%(1<<(k+1)）放入数组中，将新数组排序双指针即可。但是双指针好难写ovo，这样的复杂度是log(4e7)n常识//狗头保命

// Problem: D. Present
// Contest: Codeforces - Codeforces Round #626 (Div. 2, based on Moscow Open Olympiad in Informatics)
// URL: https://codeforces.com/contest/1323/problem/D
// Memory Limit: 512 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
typedef long long ll; 
using namespace std;
const int N=2e7+10;
int a[400010];
int n;
ll cnt[30];
int b[400010];
int main()
{
//	cout<<(1<<25)<<endl;
	ios;
	cin >> n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=25;i>=0;i--)
	{
		for(int j=1;j<=n;j++) b[j]=a[j]%(1<<(i+1));
		sort(b+1,b+1+n);
		int k=n;
		int k2=n;
		for(int j=1;j<=n;j++)
		{
			while(k>j && b[k]+b[j]>=(1<<(i+1)))	
			{
				k--;
			}
//			if(k2==j)	k2++;
			while(k2>j  && b[k2]+b[j]>=(1<<i))
			{
				k2--;
			}
			if(k2<=j && k<=j)
			{
				;
			}
			else if(k>j &&  k2<=j)
			{
				cnt[i]+=k-j;
			}
			else
			{
				cnt[i]+=k-k2;
			}
		}

		k=n;
		for(int j=1;j<=n;j++)
		{
			while(k>j && b[k]+b[j]>=((1<<(i+1)) + (1<<i)))	
			{
				k--;
			}
			if(k>j)
			cnt[i]+=n-k;
			else
			{
				cnt[i]+=n-j;
			}
		}
//		if(i<=3)
		//cout<<cnt[i]<<endl;
	}
	int res=0;
	for(int i=0;i<=25;i++)
	{
	//	cout<<i<<" "<<cnt[i]<<endl;
		if(cnt[i]&1)
		res+=1<<i;
	}

	cout<<res<<endl;
	return 0;
}