自适应辛普森积分

Posted 2021-11-05 goto_1600

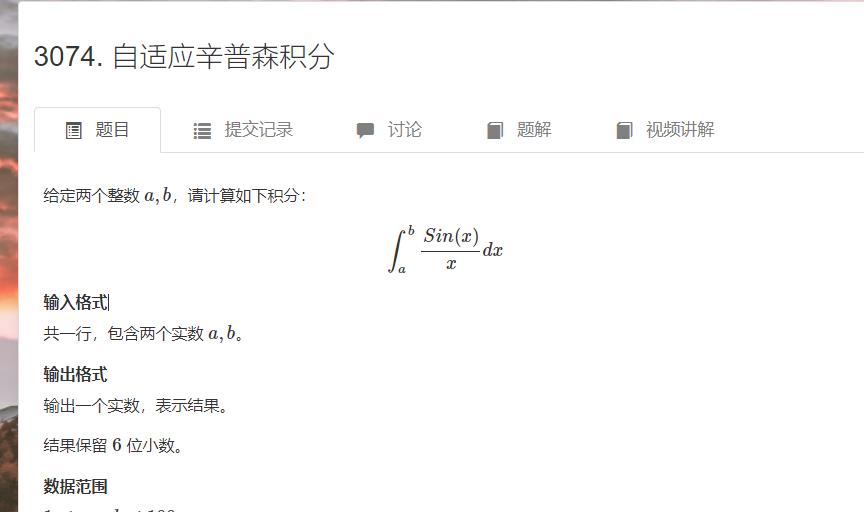
主要是要会弄出f(）值

simpson公式就是(f(l)+f®+(f(l+r)/2))*(r-l)/6

可以用的地方基本都是有弧度的曲线。

#include<iostream>
#include <cmath>

using namespace std;
const double eps = 1e-12;
double f(double x)
{
    return sin(x)/x;
}
double simpson(double l,double r)
{
    double mid=(l+r)/2;
    return (f(l)+4*f(mid)+f(r))*(r-l)/6;
}
double asr(double l,double r,double s)
{
    double mid=(l+r)/2;
    double left=simpson(l,mid);
    double right=simpson(mid,r);
    if(fabs(s-(left+right))<eps)    return left+right;
    return asr(l,mid,left)+asr(mid,r,right);
}
int main()
{
   double l,r;
   cin>>l>>r;
   printf("%.6lf\\n",asr(l,r,simpson(l,r)));
   
   return 0;
}

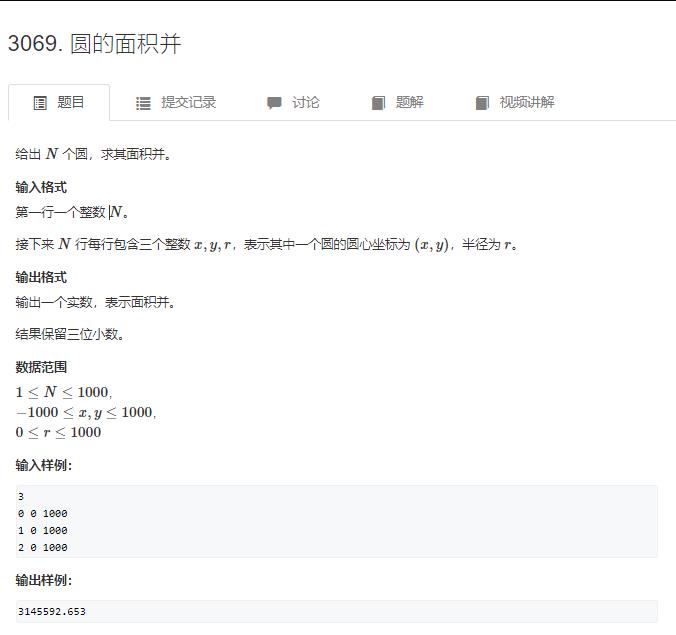
#include<iostream>
#include <cmath>
#include<algorithm>
using namespace std;
const double eps = 1e-8;
const int N=1010;
#define x first
#define y second
typedef pair<double,double> pdd;
  int n;
 int dcmp(double a,double b)
 {
     if(fabs(b-a)<eps)  return 0;
     if(a>b)    return 1;
     return -1;
 }
struct circle
{
    pdd p;
    double r;
}q[N];
pdd pp[N];
double f(double x)
{
    double res=0;
    int cnt = 0;
    for(int i=1;i<=n;i++)
    {
        pdd  p  = q[i].p;
        double r=q[i].r;
        double D=0;
        if(dcmp(r,fabs(p.x-x))==1)
        {
            D=sqrt(r*r-(p.x-x)*(p.x-x));
            pp[++cnt]={p.y-D,p.y+D};
        }
    }
    
    sort(pp+1,pp+1+cnt);
    if(!cnt)
    return 0;
    for(int i=1;i<=n;i++)
    {
      //  cout<<pp[i].x<<" "<<pp[i].y<<endl;
    }
    double ed=pp[1].y;
    double st=pp[1].x;
    for(int i=2;i<=cnt;i++)
    {
        if(pp[i].x<=ed)  ed=max(ed,pp[i].y);
        else
        {
            res+=ed-st;
            st=pp[i].x;
            ed=pp[i].y;
        }
    }
    
    return res+ed-st;
}
double simpson(double l,double r)
{
    return (f(l)+f(r)+4*f((l+r)/2))*(r-l)/6;
}
double asr(double l,double r,double s)
{
    //cout<<l<<" "<<r<<endl;
    double mid=(l+r)/2;
    double left=simpson(l,mid);
    double right=simpson(mid,r);
    if(dcmp(s,left+right)==0)   return left+right;
    else
    return asr(l,mid,left)+asr(mid,r,right);
}
int main()
{
  
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        double x,y,r;
        cin>>x>>y>>r;
        q[i]={{x,y},r};
      //  cout<<x<<" "<<y<<" "<<r<<endl;
    }
    printf("%.3lf\\n",asr(-2000,2000,simpson(-2000,2000)));
    return 0;
}