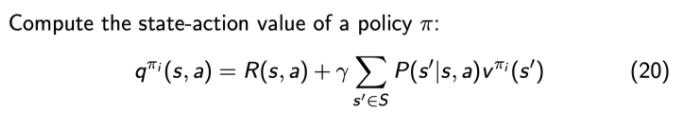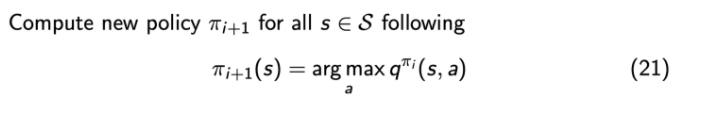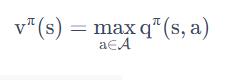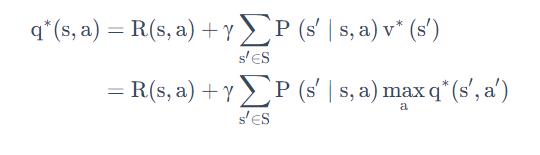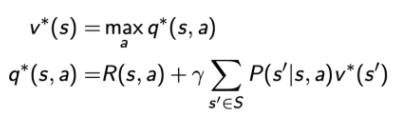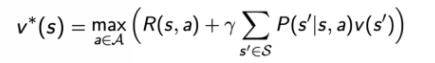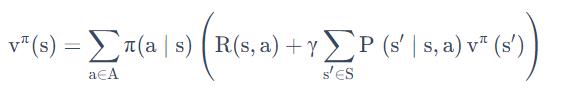强化学习笔记： MDP - Policy iteration

Posted 2021-11-04 UQI-LIUWJ

1 Policy iteration介绍

 Policy iteration式马尔可夫决策过程 MDP里面用来搜索最优策略的算法

 

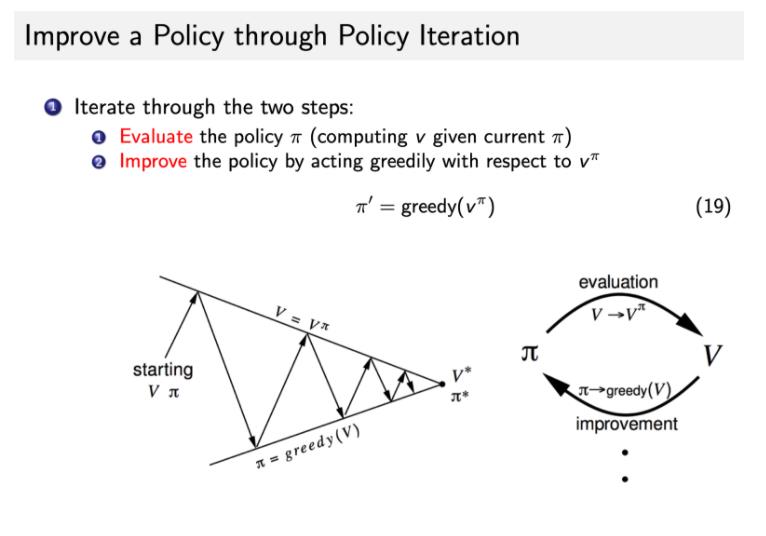
 Policy iteration 由两个步骤组成：policy evaluation 和 policy improvement。

2 Policy iteration 的两个主要步骤

        第一个步骤是 policy evaluation，当前我们在优化这个 policy π，我们先保证这个 policy 不变，然后去估计它出来的这个价值。即：给定当前的 policy function 来估计这个 v 函数

        第二个步骤是 policy improvement，得到 v 函数过后，我们可以进一步推算出它的 Q 函数。

得到 Q 函数过后，我们直接在 Q 函数上面取极大化，通过在这个 Q 函数上面做一个贪心的搜索来进一步改进它的策略。

        这两个步骤就一直是在迭代进行，所以在 policy iteration 里面，在初始化的时候，我们有一个初始化的 V和 π ，然后就是在这两个过程之间迭代。

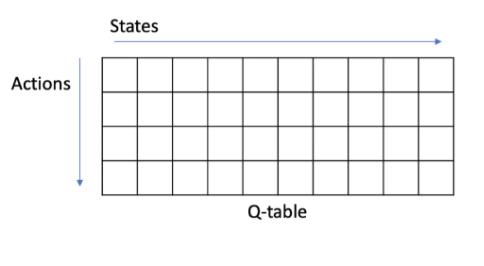
3 Q-table

把 Q 函数看成一个 Q-table,得到 Q 函数后，Q-table也就得到了。:

• 横轴是它的所有状态，
• 纵轴是它的可能的 action。

        那么对于某一个状态，每一列里面我们会取最大的那个值，最大值对应的那个 action 就是它现在应该采取的 action。

        所以 arg max 操作就说在每个状态里面采取一个 action，这个 action 是能使这一列的 Q 最大化的那个动作。

        当一直在采取 arg max 操作的时候，我们会得到一个单调的递增。

        通过采取这种 greedy，即 arg max 操作，我们就会得到更好的或者不变的 policy，而不会使它这个价值函数变差。

        所以当这个改进停止过后，我们就会得到一个最佳策略

4 Bellman Optimization Equation

对于MDP，我们知道有这样的式子

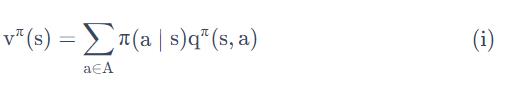
        当改进停止的时候，action的决策已经确定，此时只有一个action的 为1，其余的均为0【这样可以使得q(s,a)最大】，所以我们可以得到一个新的等式：

         这个等式被称为 Bellman optimality equation，当 MDP 满足 Bellman optimality equation 的时候，整个 MDP 已经到达最佳的状态。

        它到达最佳状态过后，对于这个 Q 函数，取它最大的 action 的那个值，就是直接等于它的最佳的 value function。

        这个等式只有当整个状态已经收敛，得到一个最佳的 policy 的时候，才会满足。

         在满足Bellman optimality equation后，我们重新审视以下Q函数的Bellman expectation equation：

         把bellman optimization equation 代入，有：

 这个式子就是Q-learning 的转移方程

 同样，对于value function的转移函数，

通过

可以推出：

【

原来的式子是：

】