2021华为杯数学建模E题思路-信号干扰下的超宽带（UWB）精确定位问题(17日更新)

Posted 2021-11-04 数模孵化园

2021华为杯数学建模E题思路 2021华为杯E题思路 信号干扰下的超宽带（UWB）精确定位问题 2021华为杯数学建模E题思路 2021华为杯E题思路 信号干扰下的超宽带（UWB）精确定位问题 2021华为杯数学建模E题思路 2021华为杯E题思路 信号干扰下的超宽带（UWB）精确定位问题 2021华为杯数学建模E题思路 2021华为杯E题思路 信号干扰下的超宽带（UWB）精确定位问题 2021华为杯数学建模E题思路 2021华为杯E题思路 信号干扰下的超宽带（UWB）精确定位问题 2021华为杯数学建模E题思路 2021华为杯E题思路 信号干扰下的超宽带（UWB）精确定位问题 

允许售卖，鼓励改进后再售卖，欢迎各位同行私信交流，有公众号或博客的，加群给管理

链接：https://pan.baidu.com/s/15SzJ-HIQiSDmME9J8Zln9g 
提取码：6epk 

第一问对数据进行处理，对于数据导入，可能很多小伙伴会觉得比较麻烦，matlab一键生成程序了解一下

 

之后就用生成的程序写个批量读取即可

生成的矩阵中，第六列(校验值)0，1，2，3分别为四个锚点，第六列为靶点到锚点的距离

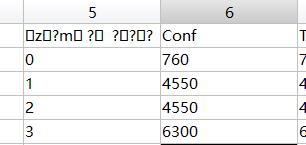
 首先来整理一下数据，得出四个锚点与靶点的距离值，这里以一个txt为例，通过下述程序，将txt文档中的数据整理成矩阵

duqu %运行生成的脚本
Untitled(1,:)=[];
X=[];m=1;
for i=1:size(Untitled,1)
    if mod(i,4)==0
        X(m,4)=double(Untitled(i,6));
        m=m+1;
    else
        X(m,mod(i,4))=double(Untitled(i,6));
    end
end

 

第二问，先说说正常txt的做法，还是以1.正常.txt为例，第一问过程中会得到n行4列的矩阵，我们绘图看看

 那么我们如何分别取出矩阵每列精准的距离数据呢，其实最简单的方式就是取平均值或者统计每行样本的出现频次，然后取占比最大的数值用于研究，当然也可以套个算法来做呢，用LOF算法，设置合适的k值，k值可以设置为样本数的1/4~1/3之间，计算的到每个点的离群度值，返回最小值的索引，对应的样本就是准确值，如果是多个索引就取平均，其实这个方法就是从数据的离散角度去确定准确值，如果是出现概率最多的数据，那么它的离群度就相对较低，这只是一个算法的活用。

%LOF算法
function lof = LOF(dist,K)
m=size(dist,1);                 %m为对象数，dist为两两之间的距离
distance = zeros(m,m);
num = zeros(m,m);               %distance 和num用来记录排序后的顺序，和对象编号顺序
kdistance = zeros(m,1);         %计算每个对象的kdistance
count  = zeros(m,1);            %k邻域的对象数
reachdist = zeros(m,m);         %计算两两之间的reachable-distance
lrd = zeros(m,1);
lof = zeros(m,1);
%计算k-距离
for i=1:m
    [distance(i,:),num(i,:)]=sort(dist(i,:),'ascend');
    kdistance(i)=distance(i,K+1); 
    count(i) = -1;%自己的距离为0，要去掉自己
    for j = 1:m
        if dist(i,j)<=kdistance(i)
            count(i) = count(i)+1;
        end
    end
end
for i = 1:m
    for j=1:i-1
        reachdist(i,j) = max(dist(i,j),kdistance(j));
        reachdist(j,i) = reachdist(i,j);
    end
end
for i = 1:m
    sum_reachdist=0;
    for j=1:count(i)
        sum_reachdist=sum_reachdist+reachdist(i,num(j+1));
    end
    %计算每个点的lrd
    lrd(i)=count(i)/sum_reachdist;
end
% 得到lof值
for i=1:m
    sumlrd=0;
    for j=1:count(i)
        sumlrd=sumlrd+lrd(num(j+1))/lrd(i);
    end
    lof(i)=sumlrd/count(i);
end
end

除了上述方法，还可以设置一个滤波器，依次遍历数据，长度设为n，那么就是依次取n个样本数据，针对每段数据求个方差，以差最小的片段样本的均值作为准确值。

正常txt比较好做，来看看异常txt

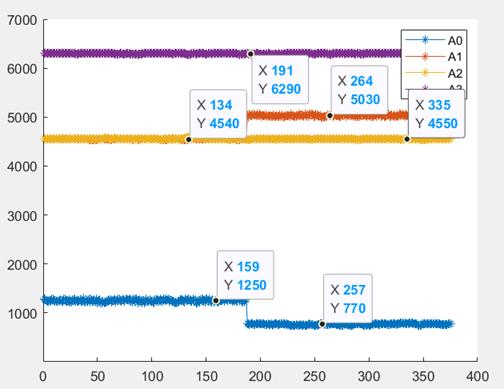
 还有这种不规整的

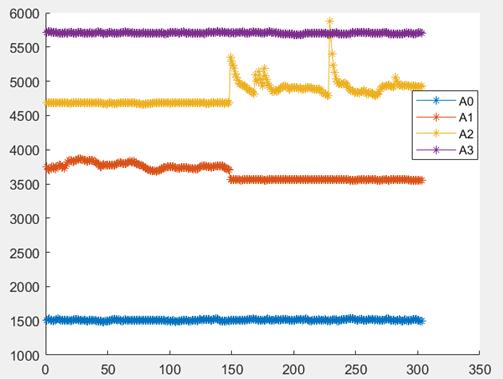
一般正常数据片段都是变化比较平稳的，针对异常txt，我们这样来设计算法，第一问中同样会将每个异常txt处理为4列数据，针对每列数据，依次从上到下遍历，每加一个数据，求一次方差，设置一个阈值，如果大于这个阈值，如果矩阵长度>100（抽取异常txt观察，其中正常的数据片段长度都是100以上），那么储存数据片段，依次类推，由于正确txt和异常txt编号一致，上面已经对每个正确txt取了A0、A1，A2，A3与靶点的距离值，然后直接匹配出与正常txt中四个距离值相近的值即可，此外，针对每个异常txt需要给出三个标注，一个是最后得到的A0、A1，A2，A3与靶点的正常距离值[770,4540,4550,6290]，然后是[1250,4540,4550,6290]、[770,5030,4550,6290]…含有异常距离的组合，这里贴标签是为了便于后续的研究

第二问剩下的就是在空间寻找最佳靶点位置的空间寻优模型，针对正常组数据，直接寻优，针对异常组数据，前面每个异常txt有三个标签，近似匹配出相应的标签，然后取出正常距离组合，寻优的话，恰好之前自创的一个优化算法的位移轨迹是空间包围型的，也恰好符合这个题目

算法程序开源的，算法名自己重新取一个，推文链接

聪明的鲨鱼(程序修改)-高维度寻优(matlab)

其中程序稍微改下就行，自变量范围改成空间的三维坐标范围，每个个体为空间一个点位，目标函数为到四个锚点距离的绝对差之和，很多小伙伴也考虑了粒子群算法，但是毕竟是老的算法，建议用新的算法比较好拿奖，之前还结合多种优化算法写的一个，也可以使用，推文链接：

动物园算法之聪明的狼-函数寻优(Matlab)

第三问，注意本问的锚点坐标改了，针对附件3，做法是同上，算出靶点位置

第四问说上述定位模型是在已知信号有、无干扰的条件下建立的，这里是不明确的，且UWB数据集也是不明确的，那么就按下述思路处理

假设没有正常和异常数据txt标注，怎么来实现区分，其实也好办，前面构建矩阵的时候，0，1，2，3标号取第六列(校验值)构成以下矩阵

 

 将四列数据拼成一列，如果是正常txt，那么DBSCAN聚类之后会得到4个类别数据组，就直接按上述方法计算出4个锚点到靶点的距离；如果异常的txt会得到多个类别数据组，接下来还是按上面说到的针对n行4列的矩阵中的每列数据，依次从上到下遍历，每加一个数据，求一次方差，设置一个阈值，如果大于这个阈值，如果矩阵长度>100（抽取异常txt观察，其中正常的数据片段长度都是100以上），那么储存数据片段，依次类推，如果恰好每列数据得到一个片段，那么直接计算出4个距离，如果有一列数据提取出2个以上数据片段，我们这里通过观察每个异常txt中，都是有两个锚点的数据是比较正常的，且A0与A2、A1与A3所处位置均是对角，我们发现A0有异常，A2就没异常，其实只要有两个锚点数据正常，那么就可以确定其他两个锚点与靶点的距离取值范围，例如下图

(既然分析到这里了，为什么不直接计算出靶点位置呢，不管是正常的距离数据，多少也有误差，况且这里只是确定范围来确定正常距离数据，所以这里仍然需要寻优最佳的靶点位置)

黄色点表示数据正常的锚点，蓝色点为数据异常的锚点，这里其实按上图只对其中一个异常锚点，确定最大最小范围，然后通过角度计算出剩下一个锚点的距离范围，也就是说剩下两个锚点的距离之间是有关系模型的，接下来对取出的每个片段计算距离数据，两个异常锚点可能分别都对应多个数值，分别取数看是否同时满足两个异常锚点的距离范围，如果都满足，那么就确定出了四个锚点到靶点正确的距离值，同样的对每个异常txt标注好正确距离和多个异常距离组。

然后针对附件4, 以上我们已经对所有txt文件进行了标注，这里给的10组数据没有说那些是异常的，那么我就就正常txt的距离取匹配，能匹配到或非常近似的，那说明没问题，如果没匹配到，那就用异常txt近似匹配出异常标注，从而输出正常距离数据，接下来还是计算靶点位置，同上

第五问，附件5是一个动态数据，处理成矩阵，绘制下

 

 

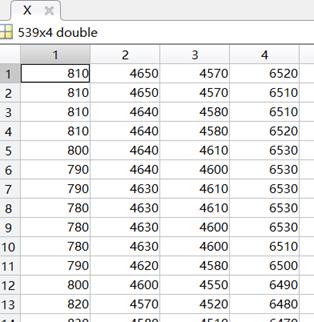
 其实我们看有异常数据的都只有一个异常，那么就好办，参照上一问的分析，直接可以对异常距离进行修正，如何判别矩阵中每行的数据是否存在异常，这里就用依次从上到下遍历，计算四个距离的变化量，开始是肯定没有异常的，设定阈值，如果其中有变化量超过这个阈值，那么说明存在异常，然后进行修正，修正之后再继续遍历下去，可能有小伙伴就说了，已经有了三个正常距离，直接算出靶点位置得了，其实这样并不严谨，要知道八点的运动轨迹应当是平滑的，接下来我们需要对修正后的每列距离值，进行平滑处理，之后再通过优化算法进行寻优靶点位置