CS224W摘要17.Scaling Up GNNs
Posted oldmao_2000
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CS224W摘要17.Scaling Up GNNs相关的知识,希望对你有一定的参考价值。
文章目录
CS224W: Machine Learning with Graphs
公式输入请参考: 在线Latex公式
这节内容貌似也很重要,是针对大规模图数据的优化。之前对这方面的了解只知道用GraphSAGE可以分Batch,貌似还有别的方法。
针对无法对GNN进行随机梯度下降的问题,搞出了GraphSAGE;
针对无法将大图直接进行full batch计算的问题,搞出了Cluster-GCN;
针对GCN模型本身进行了简化,去掉了非线性的计算,并进行了化简。
Scaling Up GNNs to Large Graphs
当前图应用的数据量
| 应用 | 数据集 | 数据量 | 常见任务 | |
|---|---|---|---|---|
| Recommender systems | Amazon YouTube | Users(绿圆): 100M~1B Products/Videos(红方):10M ~ 1B | Recommend items(link prediction) Classify users/items(node classification) | 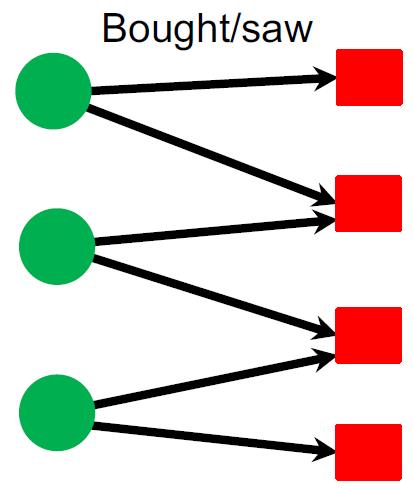 |
| Social networks | Facebook | Users:300M~3B | Friend recommendation (link-level) User property prediction(node-level) | 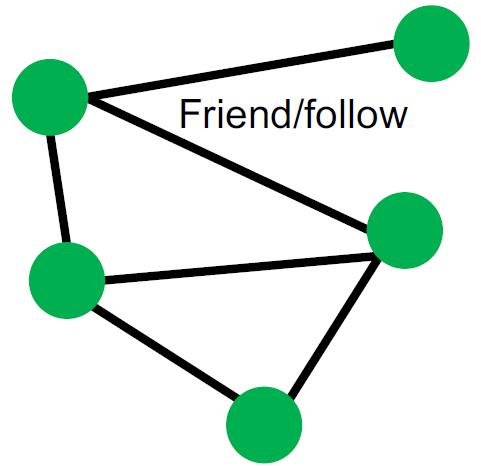 |
| Academic graph | Microsoft Academic Graph | Papers:120M Authors:120M | Paper categorization(node classification) Author collaboration recommendation Paper citation recommendation(link prediction) | 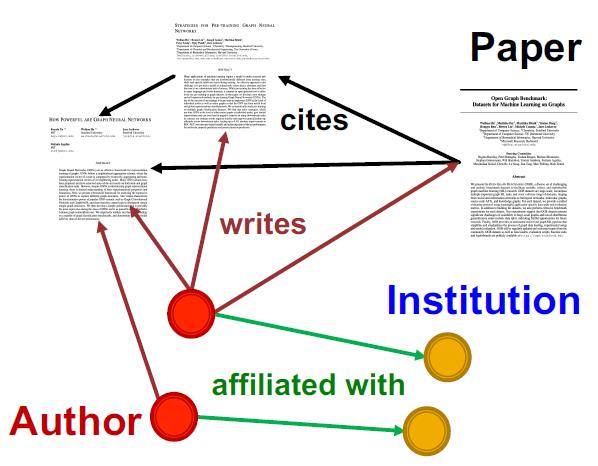 |
| Knowledge Graphs | Wikidata Freebase | Entities:80M~90M | KG completion Reasoning | 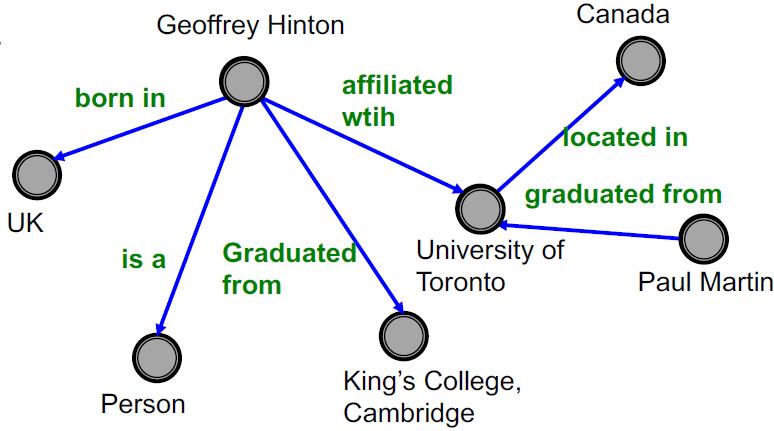 |
特点
尺寸大:节点数从10M到10B;边数量从100M到100B。
常见任务:
节点级别:User/item/paper classification
边级别:Recommendation, completion
SGD for GNN?
对于传统的ML优化方法当然就是GD:
l
(
θ
)
=
1
N
∑
i
=
0
N
−
1
l
i
(
θ
)
\\mathcal{l}(\\theta)=\\cfrac{1}{N}\\sum_{i=0}^{N-1}l_i(\\theta)
l(θ)=N1i=0∑N−1li(θ)
对于数据量较大的时候,要计算所有的点再进行梯度更新效率很低,因此常用随机梯度下降法,每次随机取
M
(
<
<
N
)
M(<<N)
M(<<N)个样本形成mini-batches,这个时候计算
M
M
M个样本的梯度
l
s
u
b
(
θ
)
l_{sub}(\\theta)
lsub(θ)更新即可:
θ
←
θ
−
▽
l
s
u
b
(
θ
)
\\theta\\leftarrow\\theta-\\triangledown l_{sub}(\\theta)
θ←θ−▽lsub(θ)
那用这个思路把SGD用在GNN上来解决GNN面临的大数据量的问题可以吗?
假设我们从图中随机取
M
(
<
<
N
)
M(<<N)
M(<<N)个独立的节点
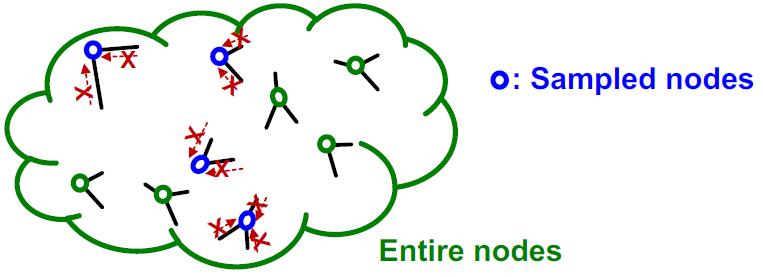
既然是独立的节点,那么采样出来的节点就是孤立的点,这样就没有办法做消息的聚合与传递了,GNN也没法玩了。
因此,原始的SGD无法用在GNN上。
Naïve full-batch implementation for GNN?
我们再看看Naïve full-batch的方式,每次生成所有节点的表征。
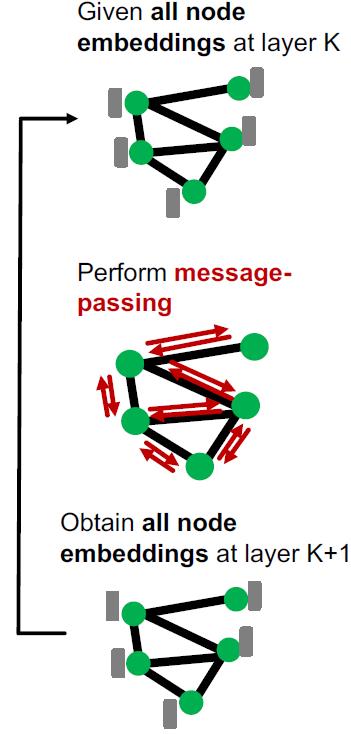
可以看到
1.训练过程需要加载全图的所有节点及特征
2.在每个GNN层中,都要基于前一层的所有节点的embedding计算当前层所有节点的embedding
3.计算损失
4.做GD
当前一般的DL都是用GPU来加速运算,GPU的内存一般是(10GB–20GB)6GB显存本本默默流泪。。。。这个数据量根本加载不进来:

看了直接硬train也不行,下面看三种解决方案。
Neighbor Sampling: GraphSAGE1
之前写过2,这里看了讲解有新的领悟,重新整理一下。
这个方法改进有三个部分:
基于邻域的随机梯度下降
SGD之所以无法用在GNN上是因为单个节点的采样会丢失邻居的信息,导致GNN的消息汇聚然并卵。
从GNN的计算图中可以看到,一个K层GNN的消息汇聚只涉及到该节点的K跳邻居:
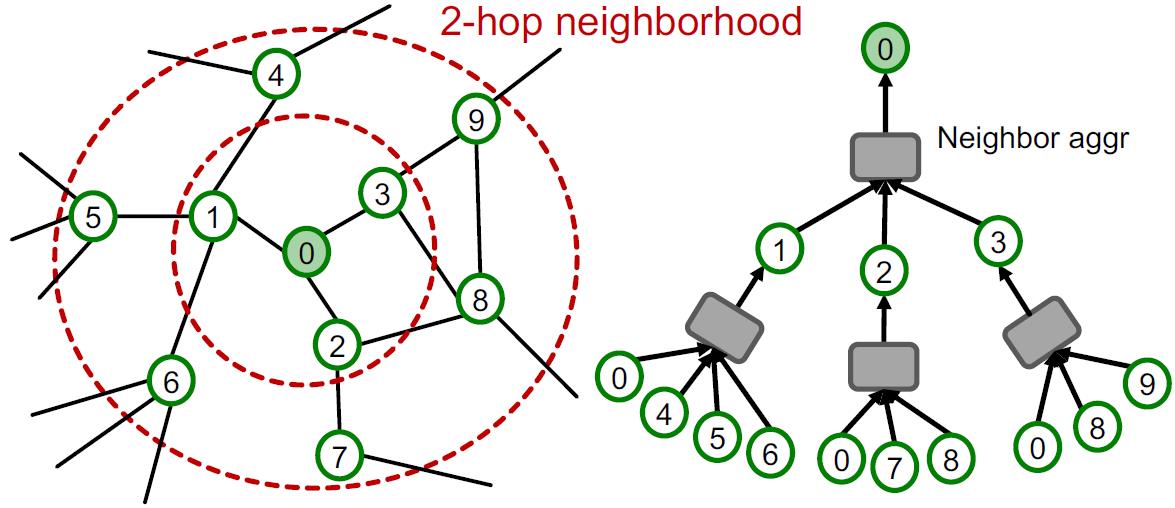
那么采样的时候不单单采样某个节点,而是直接将该节点以及其K跳邻域信息包含进来,形成mini-batch:
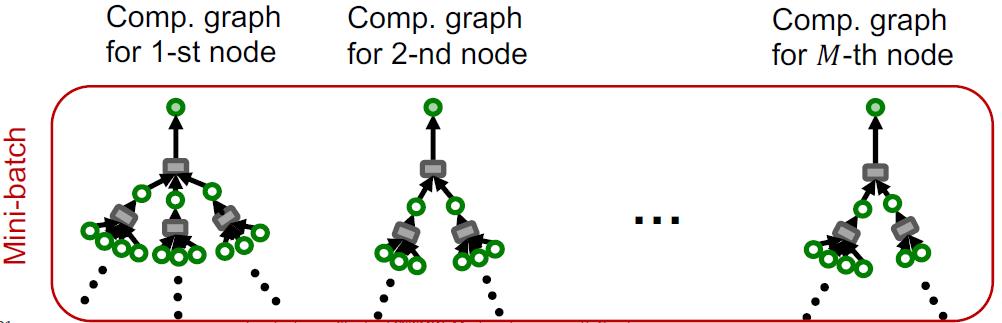
这样就得到了基于邻域的SGD算法,具体描述如下:
1.随机采样
M
(
<
<
N
)
M(<<N)
M(<<N)个节点
2.对于每个采样节点
v
v
v
2.1获取其K跳邻居,并构造计算图
2.2用计算图生成节点
v
v
v的embedding
3.计算
M
M
M个节点的梯度
l
s
u
b
(
θ
)
l_{sub}(\\theta)
lsub(θ)
4.更新梯度:
θ
←
θ
−
▽
l
s
u
b
(
θ
)
\\theta\\leftarrow\\theta-\\triangledown l_{sub}(\\theta)
θ←θ−▽lsub(θ)
好处与问题
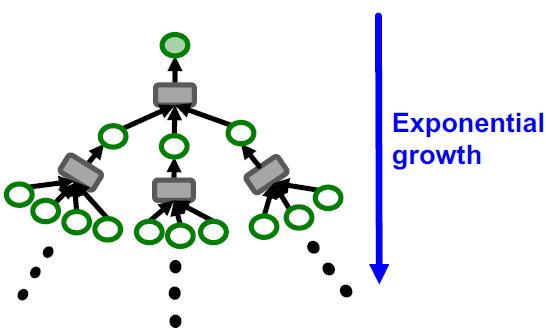
这里将计算图代替单个节点,即可实现mini-batch,又能保证图的信息汇聚不变,当然是效率提高的,但是也存在一个问题。在2.1步中,生成计算图非常耗费资源,因为图的邻居节点数量增长是K跳的指数级:
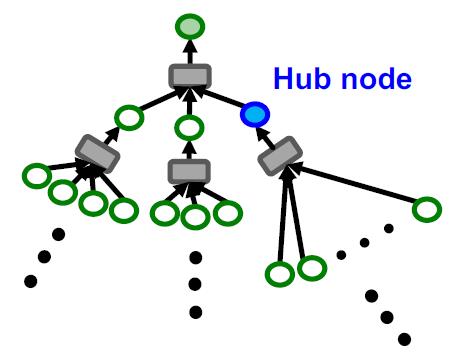
另外对于一些图中的超级节点,例如某个大V的粉丝好几百万,意味该节点的邻居超多,做2.2步的时候会很慢:
邻居采样
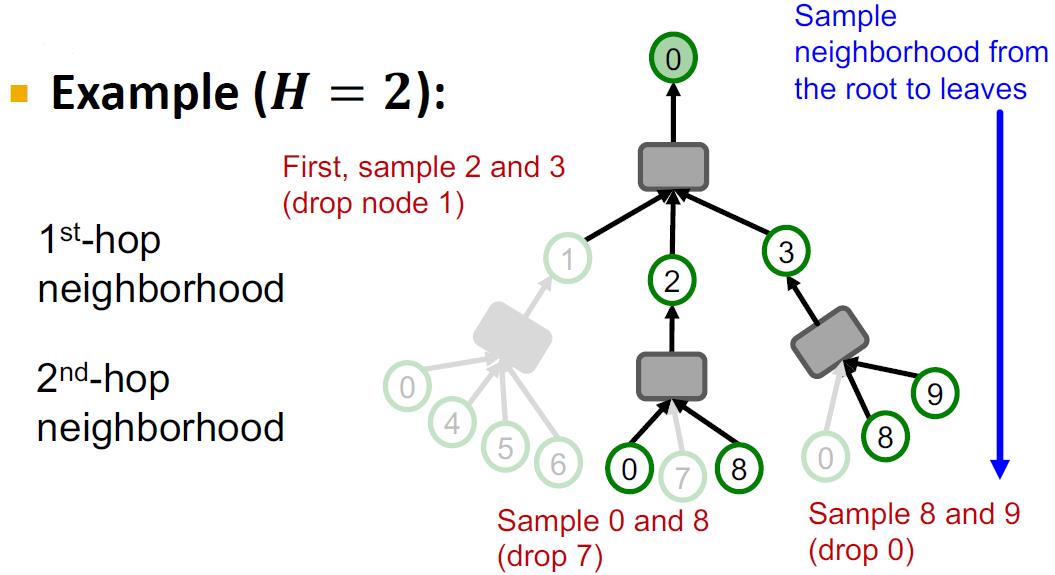
使用邻居采样进一步压缩计算图。这个也是SAGE的由来sample+aggregate。其思想就是在每跳邻居中采样
H
H
H个邻居,下面是
H
=
2
H=2
H=2的例子
邻居采样(相当于计算树剪枝)后在进行SGD。这里只需要将前面的2.1换成下面的步骤:
对于K层GNN的邻居采样描述如下:
1.对于
k
=
1
,
2
,
⋯
,
K
:
k=1,2,\\cdots,K:
k=1,2,⋯,K:
1.1对于每个第
k
k
k跳的邻居,最多随机采样
H
k
H_k
Hk个邻居
2.得到最多包含
∏
k
=
1
K
H
k
\\prod_{k=1}^KH_k
∏k=1KHk个叶子节点的计算图
好处与问题
较小的
H
H
H可以使得邻居汇聚效率大大增加,但会使得模型的训练不够稳定,因为每次随机出来邻居不一样。
虽然有了
H
H
H个邻居的上限,计算图大小的上限仍然和K跳(GNN的层数也是它)呈指数关系,K增加还是会使得计算图变很大。
最大的问题是随机采样,因为图中的节点明显有不一样的重要程度,采样到不重要的邻居得到embedding的结果明显不是最优的。
邻居的选择
为了解决随机采样的问题,这块研究还有待进一步研究,目前的解决方法是采取策略来采样重要的点:

例如上图中的策略是:
从绿色点开始可回原地随机游走,并计算Restarts score:
R
i
R_i
Ri(直觉上:这个玩意越高说明该节点涉及到的内部节点越多,就是random walk with restarts,RWR算法)
在每层GNN的邻居采样中对高
R
i
R_i
Ri的邻居采样。
小结及改进思路
该方法是目前工业上应用较成熟的方法。pintrest?阿里都在用
但是该方法仍然有一些缺点:
1.计算图的大小仍然和GNN的层数成指数关系
2.计算过程非常冗余,尤其是当邻域中多个节点共享邻居的时候(在同一个mini-batch中),该邻居会在计算图中出现多次,例如:
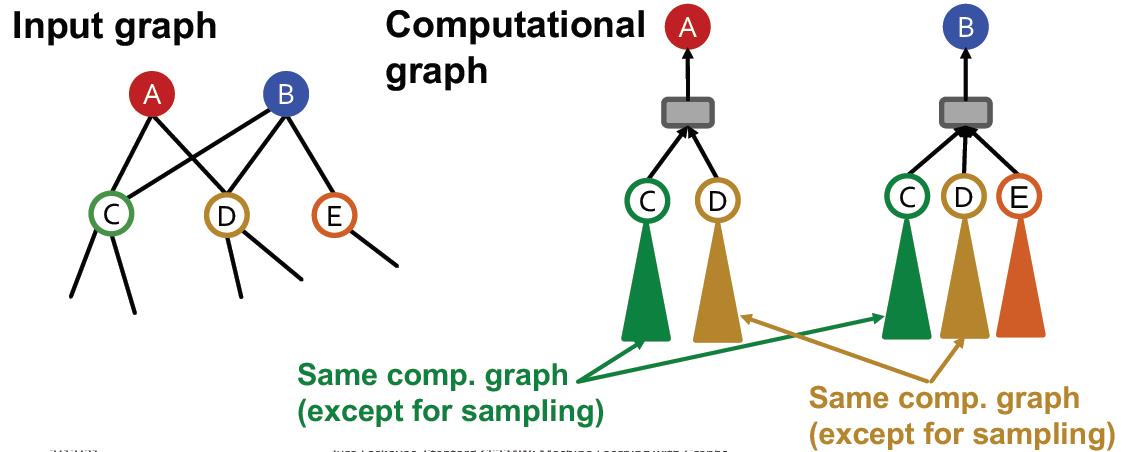
可以看到C和D都是AB的公共邻居,每个都计算了两次,考虑某个大V节点岂不是要计算很多次?
再回头看full-batch GNN的实现过程,所有的节点都用前一层的embedding结果来更新当前层的embedding,不存在上面的重复计算问题:
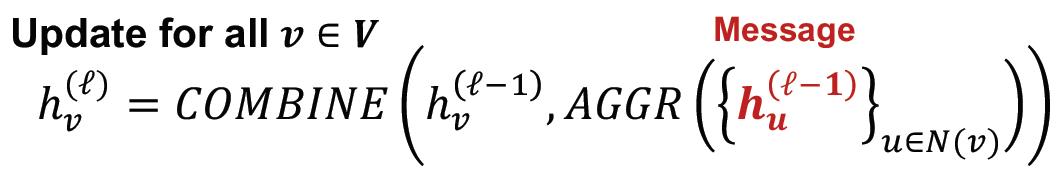
而且,从计算公式可以看到,在每一层的消息汇聚,只用计算
2
×
E
次
,
E
2\\times E次,E
2×E次,E是边数量,
u
u
u的消息汇聚给
v
v
v,
v
v
v的消息汇聚给
u
u
u:
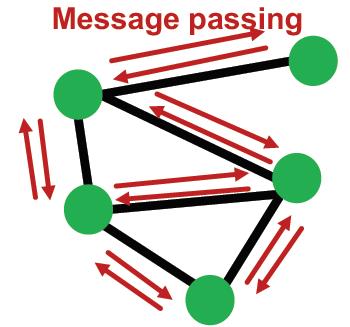
对于
K
K
K层的GNN,那么计算次数为:
2
K
E
2KE
2KE,也就是说整个计算过程的复杂度分别与层数、边数成线性关系,非常快。
也就是说full-batch GNN的layer-wise node embedding update方法可重复使用前一层的embedding结果,不需要冗余的计算和邻居的采样。但是,它的问题在于内存放不下,下面看从full-batch如何解决GNN的大图训练问题。
PS:这里还有另外一个模型HAG,层次化聚合图模型也是类似思想,用的是层次化的划分思想。
Cluster-GCN
子图采样
既然上面讨论了大图有很多优势,但是由于内存方面的限制导致这个方法无法使用,那么可以考虑将大图拆分成可以放进内存的小图,然后再计算的思路:
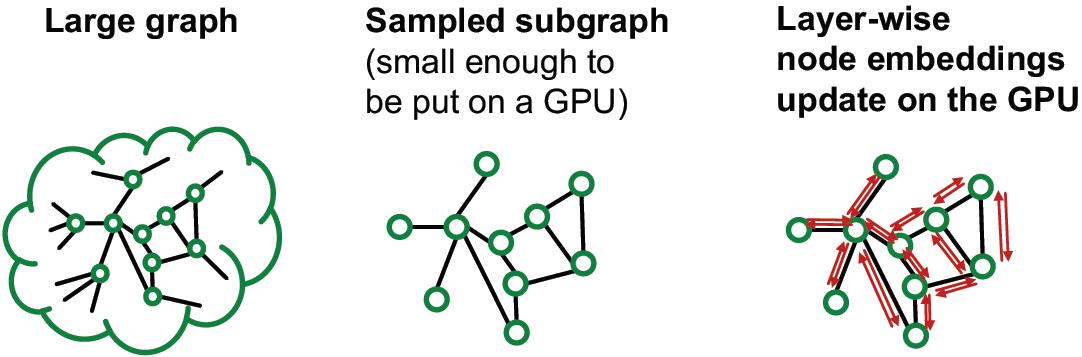
那么这里就稍微看看这个方法的可行性如何,或者说拆分后效果会不会扑街。
由于GNN的计算是基于邻居节点的消息汇聚机制的,那么,如果切分后的子图能够最大限度的保留原图的邻域信息,那么切割后子图消息汇聚产生的embedding和原图应该是差不多的。
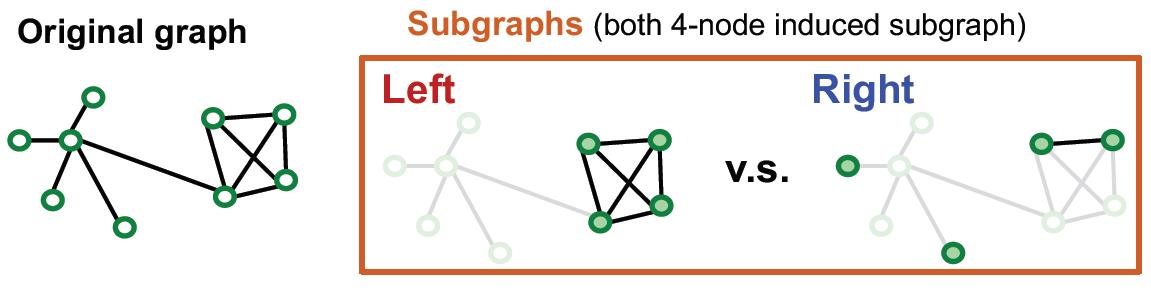
从上面的例子看,在子图采样要最大化保证原来的connectivity,分开但丢边少。
由于现实存在的图中包含较为丰富的社区结构,因此将图中的社区采样出来作为子图,每个子图可以包含原图的local connectivity pattern。
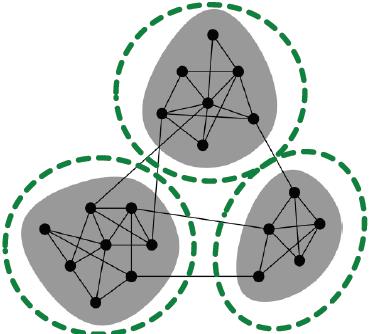
Cluster-GCN overview
给定图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),将其节点
V
V
V划分为
C
C
C个组:
V
1
,
V
2
,
⋯
,
V
C
V_1,V_2,\\cdots,V_C
V1,V2,⋯,VC
为了保证社区的完整性,可以使用已有的社区检验方法,例如:Louvain, METIS3。
每个小组的节点
V
1
,
V
2
,
⋯
,
V
C
V_1,V_2,\\cdots,V_C
V1,V2,⋯,VC生成对应的
C
C
C个子图:
G
1
,
G
2
,
⋯
,
G
C
G_1,G_2,\\cdots,G_C
G1,G2,⋯,GC,每个子图有以下关系:
G
C
≡
(
V
C
,
E
C
)
,
where
E
c
=
{
(
u
,
v
)
∣
u
,
v
∈
V
c
}
G_C\\equiv (V_C,E_C),\\\\ \\text{where }E_c=\\{(u,v)|u,v\\in V_c\\}
GC≡(VC,EC),where Ec={(u,v)∣u,v∈Vc}
每个子图之间没有边相连:
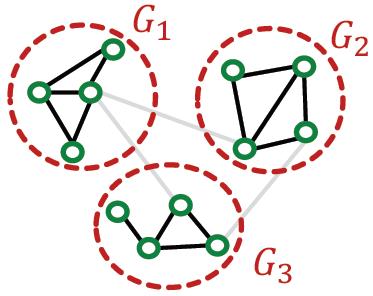
Cluster-GCN: MIni-batch Training
1.对每个mini-batch,随机采样一个节点组:
V
c
V_c
Vc
2.构造induced subgraph:
G
c
=
(
V
c
,
E
c
)
G_c= (V_c,E_c)
Gc以上是关于CS224W摘要17.Scaling Up GNNs的主要内容,如果未能解决你的问题,请参考以下文章