1310. 数三角形（组合数学）

Posted 2021-11-04 li_wen_zhuo

题目描述

给定一个 n×m 的网格，请计算三点都在格点上的三角形共有多少个。
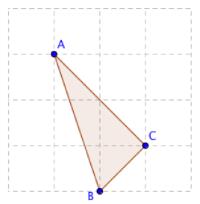
下图为 4×4 的网格上的一个三角形。

注意：三角形的三点不能共线。

输入格式

输入一行，包含两个空格分隔的正整数 m 和 n。

输出格式

输出一个正整数，为所求三角形数量。

数据范围

1≤m,n≤1000

输入样例
2 2
输出样例
76

题目分析

$我们直接算组成三角形的数量并不好算，因此我们可以反过来，先算出所有的选择，再减去其中不合法的方案$$即可。$

$首先，在网格的所有点中任取三个点的方案数为：C_{n\ast m}^3$

$然后，再减去所有不合法（三点组成一条直线）的情况：$
$1、三点组成的直线斜率为0（三个点在一行上）的情况：n\ast C_m^3（一共有n行，每行上有m个点）$
$2、三点组成的直线斜率为\infty （三个点在一列上）的情况：m\ast C_n^3（一共有m列，每列上有n个点）$

$3、三点组成的直线斜率不为0和\infty 的情况，这时的斜率分为大于0和小于0，因为这两种情况是对称的，因此我们$$只需要求出大于0的情况即可（小于0的方案数与大于0的方案数相等）。$
$我们可以枚举网格中所有低为i，高位j的斜边，该边的两个端点为三角形的两个点，第三个点在直线的内部。$
$首先，这样的直线有(n-i)\ast (m-j)个，每条直线内部第三个点的选择方案数为gcd(i,j)-1。$

$因此，对于每一个(i,j)，其方案数有：(n-i)\ast (m-j)\ast (gcd(i,j)-1)$

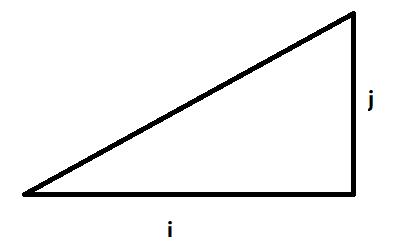
代码如下

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <map>
#include <queue>
#include <vector>
#include <bitset>
#include <set>
#include <algorithm>
#define LL long long
#define ULL unsigned long long
#define PII pair<int,int>
#define x first
#define y second
using namespace std;
const int N=1e6+5,INF=0x3f3f3f3f;
LL C(int n)						//求C(n,3)的函数，因为本题中只会用到求C(x,3)的方法
{
    return (LL)n*(n-1)*(n-2)/6;
}
int main()
{
    int n,m;
    cin>>n>>m;
    n++,m++;						//行列的点数为网格数+1
    LL ans=C(n*m)-m*C(n)-n*C(m);	//先算出所有选择减去前两种情况
    for(int i=1;i<=n;i++)			//减去第三种情况
        for(int j=1;j<=m;j++)
            ans-=2ll*(__gcd(i,j)-1)*(n-i)*(m-j);	//因为有斜率为正和负两种情况，因此还要乘2
    cout<<ans<<endl;
    return 0;
}