[人工智能-深度学习-21]：卷积神经网络CNN -- 多维输入的神经元模型及其本质：一维矩阵的点乘
Posted 文火冰糖的硅基工坊
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[人工智能-深度学习-21]：卷积神经网络CNN -- 多维输入的神经元模型及其本质：一维矩阵的点乘相关的知识，希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客
本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120795317
目录
第1章 神经元的一维输入模型
1.1 一维线性输入的原始神经元模型
https://blog.csdn.net/HiWangWenBing/article/details/120169493?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163405246716780265445855%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=163405246716780265445855&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_v29-1-120169493.pc_v2_rank_blog_default&utm_term=%E7%A5%9E%E7%BB%8F%E5%85%83&spm=1018.2226.3001.4450
就得到了最简化的模型 =》 W * X = Y
其中:
- X：为n+1长度的列矩阵
- W：为n+1长度的行矩阵
- Y：为0维的数值标量
1.2 一维输入时神经元的张量运算模型
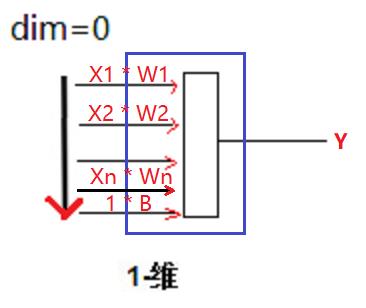
1.3 一维输入时神经元的代码示例
print("定义一维格式的输入数据")
x1 = np.array([0,1,1,1])
print("x.shape=",x1.shape)
print("x=\\n",x1)
print("")
print("定义一维格式的神经元参数")
w1 = np.array([1,0,0,1])
print("w.shape=",w1.shape)
print("w=\\n",w1)
print("")
print("W * X的线性运算")
z = w1 * x1
print("z.shape=", z.shape)
print("z=\\n",z)
print("")
print("累加和的神经元输出")
y = np.sum(z)
print("y.shape=", y.shape)
print("y=",y)定义一维格式的输入数据 x.shape= (4,) x= [0 1 1 1] 定义一维格式的神经元参数 w.shape= (4,) w= [1 0 0 1] W * X的线性运算 z.shape= (4,) z= [0 0 0 1] 累加和的神经元输出 y.shape= () y= 1
1.4 一维输入神经元的内积运算
x = x1
w = w1
print("x.shape=",x.shape)
print("x=\\n",x)
print("")
print("w.shape=",w.shape)
print("w=\\n",w)
print("")
print("w, w的dot运算")
y = np.dot(x, w)
print("y.shape=", y.shape)
print("y=",y)
print("")
print("x, w的matmul运算")
y = np.matmul(x, w)
print("y.shape=", y.shape)
print("y=",y)
print("")
print("x, w的matmul运算")
y = np.multiply(x, w)
print("y.shape=", y.shape)
print("y=",y)x.shape= (4,) x= [0 1 1 1] w.shape= (4,) w= [1 0 0 1] w, w的dot运算 y.shape= () y= 1 x, w的matmul运算 y.shape= () y= 1 x, w的matmul运算 y.shape= (4,) y= [0 0 0 1]
第2章 神经元的二维输入模型
2.1 二维张量输入的神经元模型
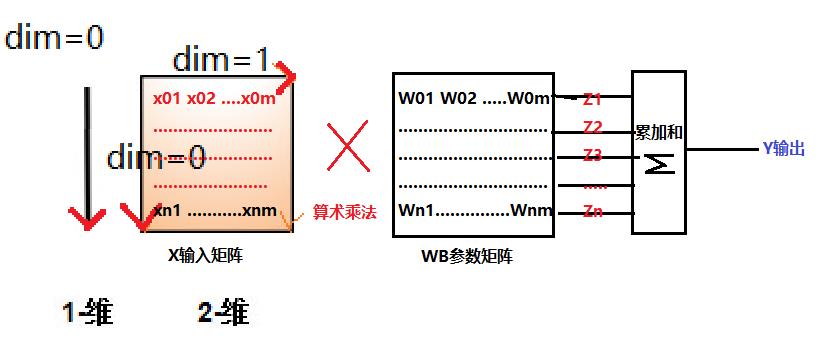
2.2 二维输入时神经元的代码示例
print("定义二维格式的输入数据")
print("把一维数据扩展成二维数据")
x2 = np.expand_dims(x1,0)
print("把一维数据复制到新扩展的二维空间")
x2 = np.repeat(x2,len(x1),axis=0)
print("x.shape=",x2.shape)
print("x=\\n",x2)
print("")
print("定义二维格式的神经元参数")
print("把一维参数扩展成二维参数")
w2 = np.expand_dims(w1,0)
print("把一维参数复制到新扩展的二维空间")
w2 = np.repeat(w2, len(x1), axis=0)
print("w.shape=",w2.shape)
print("w=\\n",w2)
print("")
print("W * X的线性运算")
z = w2 * x2
print("z.shape=", z.shape)
print("z=\\n",z)
print("")
print("累加和的神经元输出")
y = np.sum(z)
print("y.shape=", y.shape)
print("y=",y)输出：
定义二维格式的输入数据 把一维数据扩展成二维数据 把一维数据复制到新扩展的二维空间 x.shape= (4, 4) x= [[0 1 1 1] [0 1 1 1] [0 1 1 1] [0 1 1 1]] 定义二维格式的神经元参数 把一维参数扩展成二维参数 把一维参数复制到新扩展的二维空间 w.shape= (4, 4) w= [[1 0 0 1] [1 0 0 1] [1 0 0 1] [1 0 0 1]] W * X的线性运算 z.shape= (4, 4) z= [[0 0 0 1] [0 0 0 1] [0 0 0 1] [0 0 0 1]] 累加和的神经元输出 y.shape= () y= 4
2.3 二元输入展开成一维输入的代码示例
print("把二维展现成一维输入数据")
x = x2.reshape(-1)
print("x2.shape=",x.shape)
print("x2=\\n",x)
print("")
print("把二维展现成一维神经元参数")
w = w2.reshape(-1)
print("w.shape=",w.shape)
print("w=\\n",w)
print("")
print("W * X的线性运算")
z = w * x
print("z.shape=", z.shape)
print("z=\\n",z)
print("")
print("累加和的神经元输出")
y = np.sum(z)
print("y.shape=", y.shape)
print("y=",y)把二维展现成一维输入数据 x2.shape= (16,) x2= [0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1] 把二维展现成一维神经元参数 w.shape= (16,) w= [1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1] W * X的线性运算 z.shape= (16,) z= [0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1] 累加和的神经元输出 y.shape= () y= 4
2.4 一维输入神经元的内积运算
print("x.shape=",x.shape)
print("x=\\n",x)
print("")
print("w.shape=",w.shape)
print("w=\\n",w)
print("")
print("w, w的dot运算")
y = np.dot(x, w)
print("y.shape=", y.shape)
print("y=",y)
print("")
print("x, w的matmul运算")
y = np.matmul(x, w)
print("y.shape=", y.shape)
print("y=",y)
print("")
print("x, w的multiply运算（不是神经元的形态，仅仅作为比较）")
y = np.multiply(x, w)
print("y.shape=", y.shape)
print("y=",y)x.shape= (16,) x= [0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1] w.shape= (16,) w= [1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1] w, w的dot运算 y.shape= () y= 4 x, w的matmul运算 y.shape= () y= 4 x, w的multiply运算（不是神经元的形态，仅仅作为比较） y.shape= (16,) y= [0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1]
第3章 神经元的三维输入模型
3.1 三维张量输入的神经元模型
3.2 二维输入时神经元的代码示例
print("定义三维格式的输入数据")
print("把二维数据扩展成三维数据")
x3 = np.expand_dims(x2, 0)
print("把二维数据复制到新扩展的三维空间")
x3 = np.repeat(x3, 3, axis=0)
print("x.shape=",x3.shape)
print("x=\\n",x3)
print("")
print("定义三维格式的神经元参数")
print("把二维参数扩展成三维参数")
w3 = np.expand_dims(w2, 0)
print("把二维参数复制到新扩展的三维空间")
w3 = np.repeat(w3, 3,axis=0)
print("w.shape=",w3.shape)
print("w=\\n",w3)
print("")
print("W * X的线性运算")
z = w3 * x3
print("z.shape=", z.shape)
print("z=\\n",z)
print("")
print("累加和的神经元输出")
y = np.sum(z)
print("y.shape=", y.shape)
print("y=",y)定义三维格式的输入数据
把二维数据扩展成三维数据
把二维数据复制到新扩展的三维空间
x.shape= (3, 4, 4)
x=
[[[0 1 1 1]
[0 1 1 1]
[0 1 1 1]
[0 1 1 1]]
[[0 1 1 1]
[0 1 1 1]
[0 1 1 1]
[0 1 1 1]]
[[0 1 1 1]
[0 1 1 1]
[0 1 1 1]
[0 1 1 1]]]
定义三维格式的神经元参数
把二维参数扩展成三维参数
把二维参数复制到新扩展的三维空间
w.shape= (3, 4, 4)
w=
[[[1 0 0 1]
[1 0 0 1]
[1 0 0 1]
[1 0 0 1]]
[[1 0 0 1]
[1 0 0 1]
[1 0 0 1]
[1 0 0 1]]
[[1 0 0 1]
[1 0 0 1]
[1 0 0 1]
[1 0 0 1]]]
W * X的线性运算
z.shape= (3, 4, 4)
z=
[[[0 0 0 1]
[0 0 0 1]
[0 0 0 1]
[0 0 0 1]]
[[0 0 0 1]
[0 0 0 1]
[0 0 0 1]
[0 0 0 1]]
[[0 0 0 1]
[0 0 0 1]
[0 0 0 1]
[0 0 0 1]]]
累加和的神经元输出
y.shape= ()
y= 12
3.3 二元输入展开成一维输入的代码示例
print("把二维展现成一维输入数据")
x = x3.reshape(-1)
print("x.shape=",x.shape)
print("x=\\n",x)
print("")
print("把二维展现成一维神经元参数")
w = w3.reshape(-1)
print("w.shape=",w.shape)
print("w=\\n",w)
print("")
print("W * X的线性运算")
z = w * x
print("z.shape=", z.shape)
print("z=\\n",z)
print("")
print("累加和的神经元输出")
y = np.sum(z)
print("y.shape=", y.shape)
print("y=",y)把二维展现成一维输入数据
x.shape= (48,)
x=
[0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0
1 1 1 0 1 1 1 0 1 1 1]
把二维展现成一维神经元参数
w.shape= (48,)
w=
[1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
0 0 1 1 0 0 1 1 0 0 1]
W * X的线性运算
z.shape= (48,)
z=
[0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0 0 0 1]
累加和的神经元输出
y.shape= ()
y= 12
2.4 一维输入神经元的内积运算
print("x.shape=",x.shape)
print("x=\\n",x)
print("")
print("w.shape=",w.shape)
print("w=\\n",w)
print("")
print("w, w的dot运算")
y = np.dot(x, w)
print("y.shape=", y.shape)
print("y=",y)
print("")
print("x, w的matmul运算")
y = np.matmul(x, w)
print("y.shape=", y.shape)
print("y=",y)
print("")
print("x, w的matmul运算")
y = np.multiply(x, w)
print("y.shape=", y.shape)
print("y=",y)x.shape= (48,) x= [0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1] w.shape= (48,) w= [1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1] w, w的dot运算 y.shape= () y= 12 x, w的matmul运算 y.shape= () y= 12 x, w的matmul运算 y.shape= (48,) y= [0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1]
第4章 神经元的本质
4.1 综合综述
（1）W*X之间的乘法是算术乘，即按位相乘！！！
（2）相乘后的累加和为神经元的输出
（3）展开前后的运算不变，指示输入形式的改变。
（4）展开前后的结果不变。
（5）为了支持多个神经元构成的神经网络运算，无论神经元的输入形式是什么（一维、二维图片、三维图片），通常会展开成一维形式。
（6）无论输入形式如何变化，无论W，B的矩阵如何变化，输出只有一路，即为所有Wi * Xi的累加和！！！！！
4.2 神经元数学运算的本质
（1）多维输入形式是的本质：算术乘+累加和
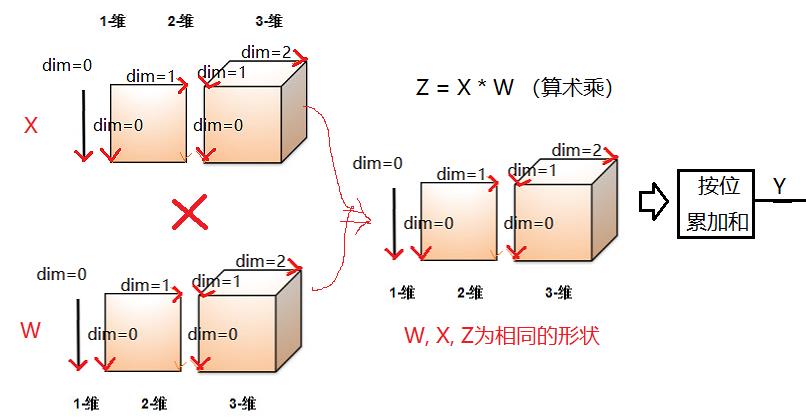
（2）转换成一维输入形式后的本质：一维矩阵的点乘（内积）
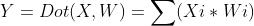
备注：在后续的讨论中，无论神经元的输入形式如何，都会转换成一维输入模型。
（3）多样本输入并发运算的模型
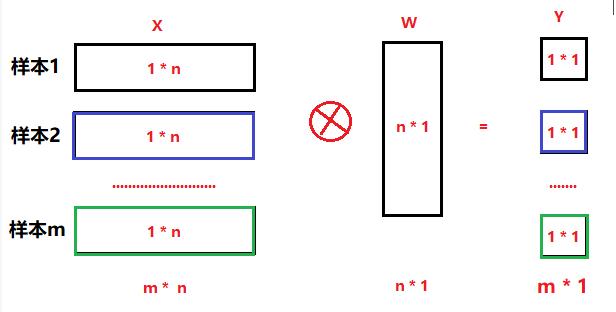
（4）单样本，多个神经元输出并发运算的模型
（4）多样本，多个神经元输出并发运算的模型
作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客
本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120795317
以上是关于[人工智能-深度学习-21]：卷积神经网络CNN -- 多维输入的神经元模型及其本质：一维矩阵的点乘的主要内容，如果未能解决你的问题，请参考以下文章
[人工智能-深度学习-24]：卷积神经网络CNN - CS231n解读 - 卷积神经网络基本层级
[人工智能-深度学习-37]：卷积神经网络CNN - 重构神经网络的疑惑与思考？
[人工智能-深度学习-26]：卷积神经网络CNN - 为啥要卷积神经网络以及卷积神经网络的应用
[人工智能-深度学习-28]：卷积神经网络CNN - 网络架构与描述方法