[人工智能-深度学习-23]：卷积神经网络CNN - 卷积核的本质是多维输入的神经元
Posted 文火冰糖的硅基工坊
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[人工智能-深度学习-23]：卷积神经网络CNN - 卷积核的本质是多维输入的神经元相关的知识，希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客
本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120734529
目录
2.2 卷积核的本质是：三维（长度 * 宽度 * 通道）输入的神经元
第1章 预备核心概念
1.1 单个神经元的一维矩阵运算模型
https://blog.csdn.net/HiWangWenBing/article/details/1207953171.2 神经网络（多个神经元）的二维矩阵运算模型
第2章 单个卷积核的本质是一个神经元
2.1 卷积核的来源
卷积来自于卷积神经网络，而卷积神经网络中核心是卷积层，卷积层的核心是卷积核，卷积层是由多个卷积核组成的神经网络。
卷积核的维度是3维：图片像素的长度 、宽度 、通道数这三个维度。
卷积核每个维度的长度（size）：并不是整个图片每个维度的长度，而是卷积核本身每个维度的长度。如下图所示，红色的圆圈就是一个卷积核。
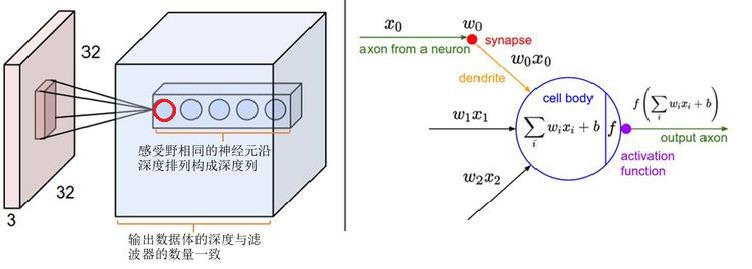
2.2 卷积核的本质是：三维（长度 * 宽度 * 通道）输入的神经元
卷积核首先是一个三个维度输入形态的神经元，如下图所示：
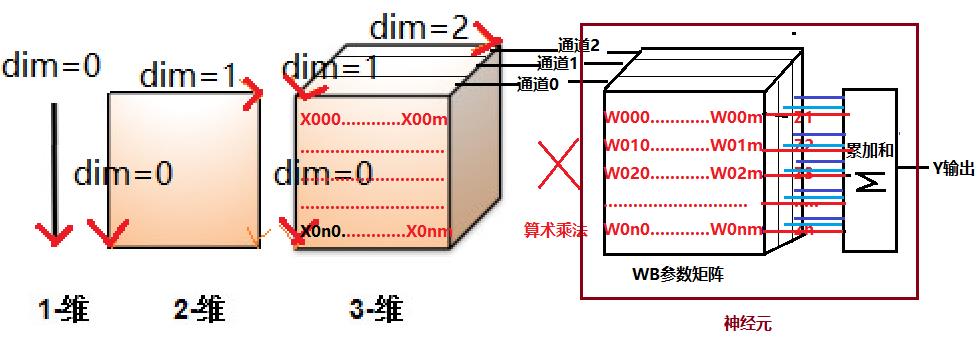
由于卷积核在x轴和y轴方向上，其长度都远远小于原始图片本身的长度。
因此，卷积核本身并没有与原始的输入的所有像素相连，而是部分相连，卷积核的参数矩阵的形状，决定了与之连接的输入属性的形状（维度+每个维度的长度）。
卷积核的大小又称为感受野（野：范围），它是指卷积核一次运算所能感受到输入属性的大小，这个大小远远小于图片本身的大小。
2.3 卷积核的直观运算：“积” = 算术乘 + 累加和
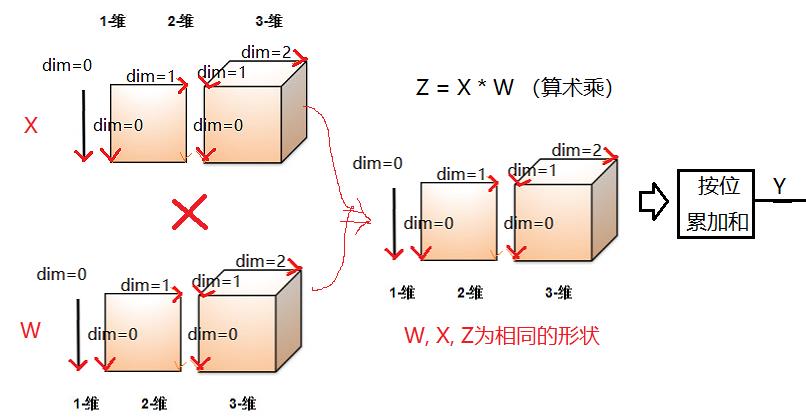
备注：
假设图片的张量为：64 * 64 * 3
假设图片的张量为： 5 * 5 * 3
则卷积核神经元的W矩阵为： 5 * 5 * 3 （暂忽略参数b）
那么卷积核的运算是：
（1）按位矩阵的算术乘：Z（5 * 5 * 3) = X (5 * 5 * 3) * W (5 * 5 * 3)
（2）对矩阵的所有位进行累加和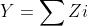 
2.4 卷积核线性化后的运算：“积” = 一维矩阵相乘
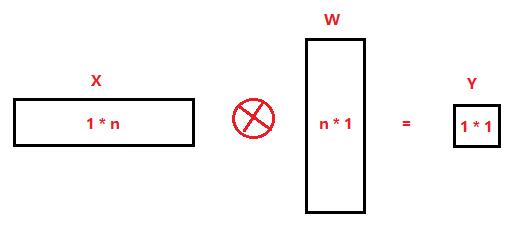
假设卷积核为（5 * 5 * 3），则：
n = 5 * 5 * 3 = 45
x 是(1 * 45) 矩阵，矩阵的像素值来自于与整个原始图片的部分输入。
w 是(45 * 1)矩阵，参数的形状（shape）决定了W参数的个数，也决定了一次性与该神经元连接的输入属性的个数。
Y 是(1 * 1) 矩阵，一个卷积核为一个神经元，一个输出。
第3章 卷积运算平移：“卷”
3.1 卷积过程
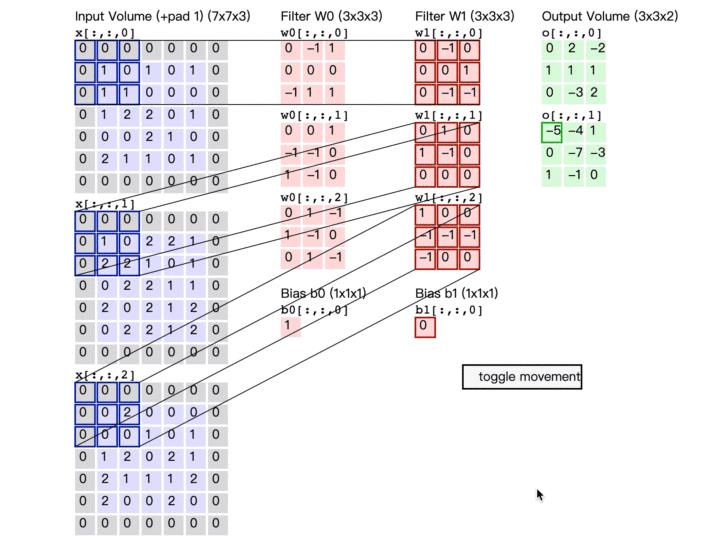
3.2卷积的串行计算法：循环法
循环法比较直观，就是执行多次循环：
（1）每一次执行一次“内积”的运算，每一次内积就是一次神经元的运算。
（2）存储一次执行结果（内积）
（3）按照步长，移动输入数据指针，选择新一批与感受野大小相等的数据。
（4）重复1-3操作，直到完成所有步长（完成“卷”的过程）
这种方法的优点：
- 简单
- 直观
- 节省内存（内存复用，用时间换区空间）
这种方法的缺点：
- 串行执行，非并行执行，执行效率低下。
3.3 卷积的并行计算法：批量样本扩展法
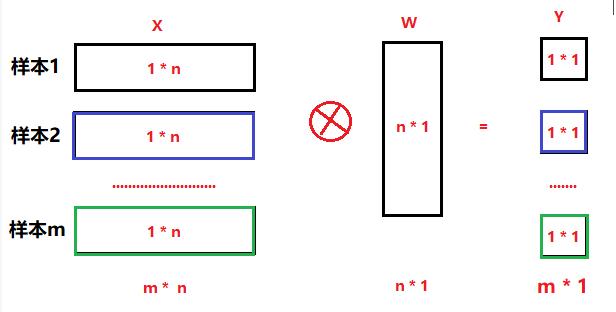
（1）扩展步骤：
- 把整个图片展现成一维数据
- 上图中样本1->n，并不是不同的样本图片数据，而是一张图片中的子图片，即部分数据。
- 根据相邻子图片之间的重叠关系（即步长与卷积核的大小关系）由分为三种情形。
（2）扩展类型
- 不重叠，中间也没有间隔：构建的扩展网络的连接数与全连接网络的连接数相同, 如下图所示：
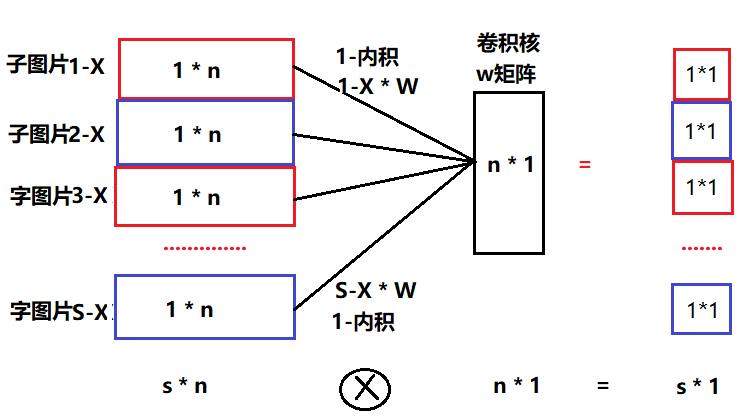
从计算量角度看, 这种方式类似于全连接，神经元与所有的输入数据进行一次计算。
但从网络结构来看，又不同于全连接：
a) W, B参数的个数不同于全连接，每个样本与神经元计算时，共享相同的W参数。
b) 输出个数：全连接模式是只有一个输出，多样本模式有多个不同的输出。
- 不重叠，中间有间隔：构建的扩展网络连接数小于全连接网络的的连接数
- 重叠：构建的扩展网络连接数大于全连接网络的连接数
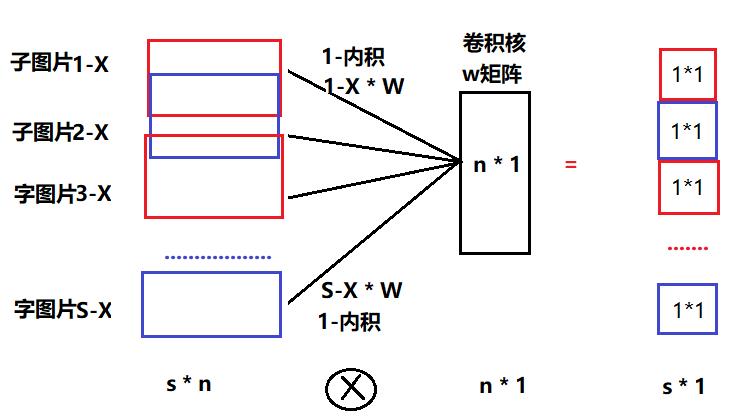
3.4 卷积神经元的本质：三维输入，二维输出的神经元。
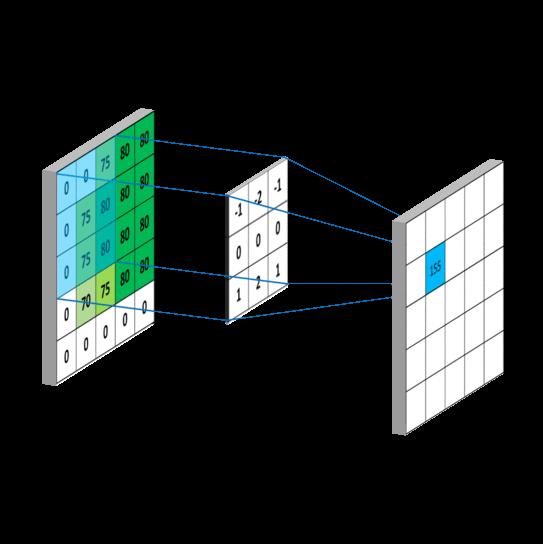
“卷”：把输入尺寸变换成输出尺寸：长度1 * 宽度1 =》 长度2 * 宽度2
“积”：把三维的卷积核大小的数据“积”（合并）成一个点。
卷积神经元是：三维输入 (X, Y, Z)，通过动态“卷积”的方式，实现二维输出（X,Y）的神经元。
全连接神经元是：一维输入（X * Y * Z)，通过静态“内积”的方式，实现一维单点输出(1*1)的神经元。
第4章 多个卷积核卷积神经网络
4.1 多个卷积核并发计算的原理
每个卷积核相当于一个神经元，多个卷积核与多个“子样本”组成如下能够支持并发运算的神经网络。
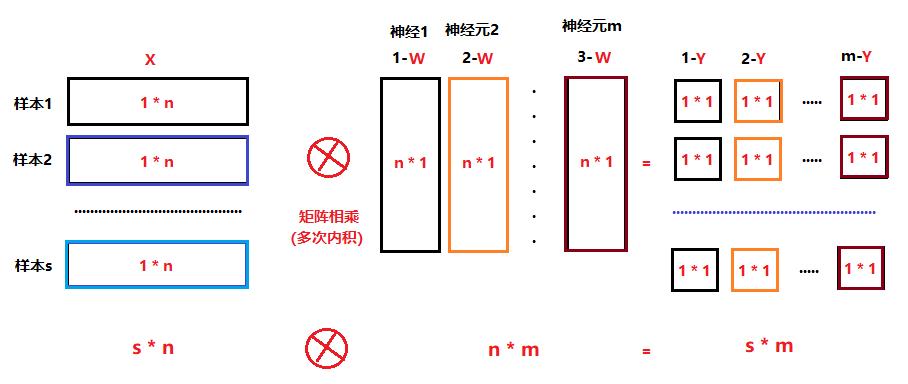
（1）图中的“样本“就是一个子图片，与卷积核感受野的大小相当，所有的子图片组合成一张大图片。
（2）图中的神经元就是”卷积核“，每一路卷积核都有一组输出，而不是一个输出，输出的个数取决于卷积的次数。
（3）卷积中的“卷”的过程，就是用小尺寸的卷积核，发现或过滤大图片中一个个小区间的特征。
（3）每个卷积核的一个个的卷积输出，本质就是发现一张图片中的一个个“小图片/子图片”的规律或输出特征。
（4）不同卷积核的每一次卷积输出，本质就是发现一张图片中的一个个“小图片/子图片"的不同规律或不同输出特征。
4.2 卷积神经网络与全连接神经网络
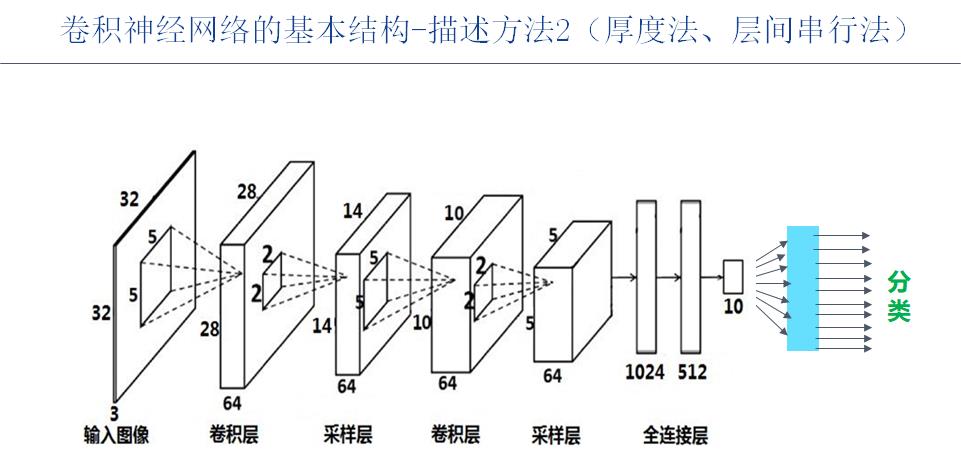
（1）卷积神经元网络是：
- 三维输入 (X, Y, Z)
- 通过动态、并行“卷积”的方式，实现三维输出（X,Y, Z）的神经元。
- 由卷积核尺寸、移动步长、填充大小决定输出支持（X,Y) ,
- 卷积核的个数决定输出尺寸（Z）。
（2）全连接神经元是：
- 一维输入 （X * Y * Z），等效的三维输入为(X, Y, Z)。
- 通过静态、并行“内积”的方式，实现一维多点输出（Z), 等效的三维输出为(1*1*Z)的神经元。
- 由全连接的一次性全累加和的方式，决定单个神经元的输出（1*1）
- 神经元的个数决定输出尺寸（Z）。
至于，如何对卷积核的一个个的输出进行一下一步的处理（比如挑选出较大的一个或求平均），就是pool层的任务了。其网络的基本原理卷积核一致。
作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客
本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120734529
以上是关于[人工智能-深度学习-23]：卷积神经网络CNN - 卷积核的本质是多维输入的神经元的主要内容，如果未能解决你的问题，请参考以下文章
深度学习100例-卷积神经网络（CNN）3D医疗影像识别 | 第23天
[人工智能-深度学习-25]：卷积神经网络CNN - CS231n解读 - 卷积层详解
[人工智能-深度学习-37]：卷积神经网络CNN - 重构神经网络的疑惑与思考？
[人工智能-深度学习-26]：卷积神经网络CNN - 为啥要卷积神经网络以及卷积神经网络的应用