week 3——Logistic Regression

Posted 2021-11-03 ^_^|

分类问题有别于回归问题，假设我们做一个二分类，我们将分类结果表示为y = 0或 y = 1。当我们尝试用回归模型去解决分类问题，我们得到的预测函数很大可能会出现$h_{\theta }(x)>1or{h}_{\theta }(x)<0$ 这样的情况，显然这是不需要的，并且不太靠谱。
我们应该尝试将$h_{\theta }(x)$ 控制在(0,1)之间，从而用以解释发生某事的概率，这样更具有可解读性。

假设（预测）函数表示

在回归问题中 $h_{\theta }(x)={\theta }^{T}x$
而逻辑回归中 令$h_{\theta }(x)=g({\theta }^{T}x),其中g(x)=\frac{1}{1+e^{-x}}$

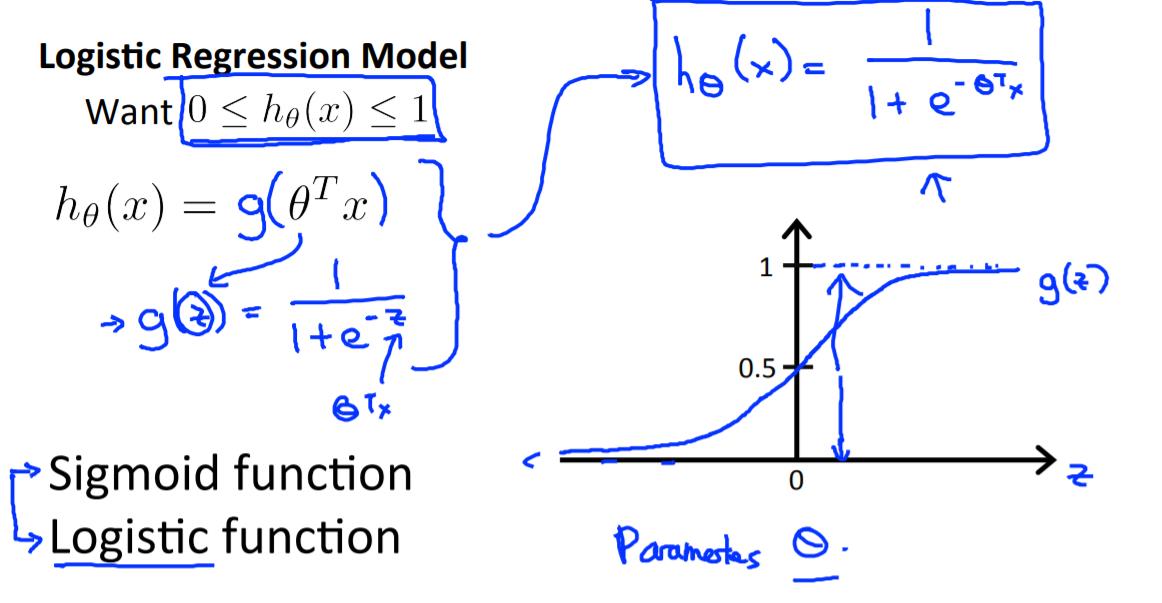
从sigmoid函数图像可以看出，其值在(0,1)间，从而$h_{\theta }\in (0,1)$, 并对$h_{\theta }(x)$作如下概率上的解释：

非线性决策边界

对于线性不可分的情况，我们一般给他加以非线性的特征，从而能够有更加丰富的决策边界划分

损失函数

逻辑回归的损失函数将不同于先前我们学习的线性回归

可见，如果继续采用线性回归中的平方和损失函数，会出现很多局部最优解，不利于模型的求解，我们希望能够找到一个相对”convex“的损失函数。
从而我们引入如下的损失函数，并对此损失函数做分析：


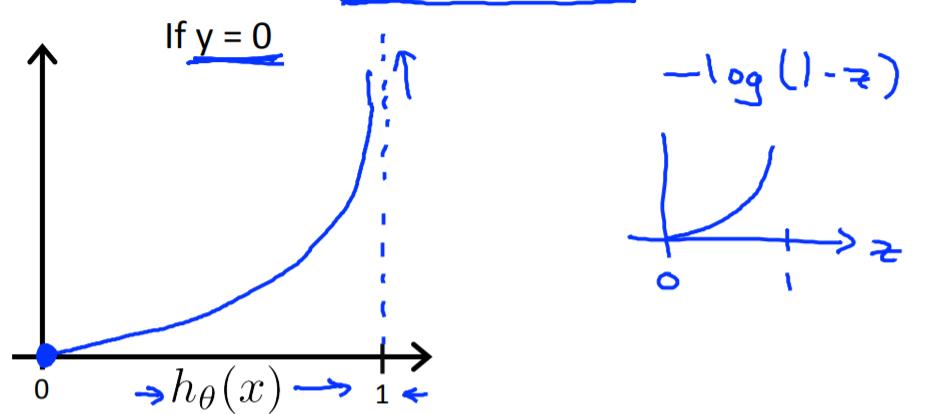
对于上述这样一个损失函数，可以看出，当y=1时，$h_{\theta }(x)$ 如果预测的值越接近1，那么损失函数就越接近于0；当y=0是，$h_{\theta }(x)$ 如果预测的越接近0，则损失函数越接近0。如此，这样的一个损失函数是”convex“的。
将上述分段函数形式的损失函数简化成一个函数，就成了下面的形式：

梯度下降

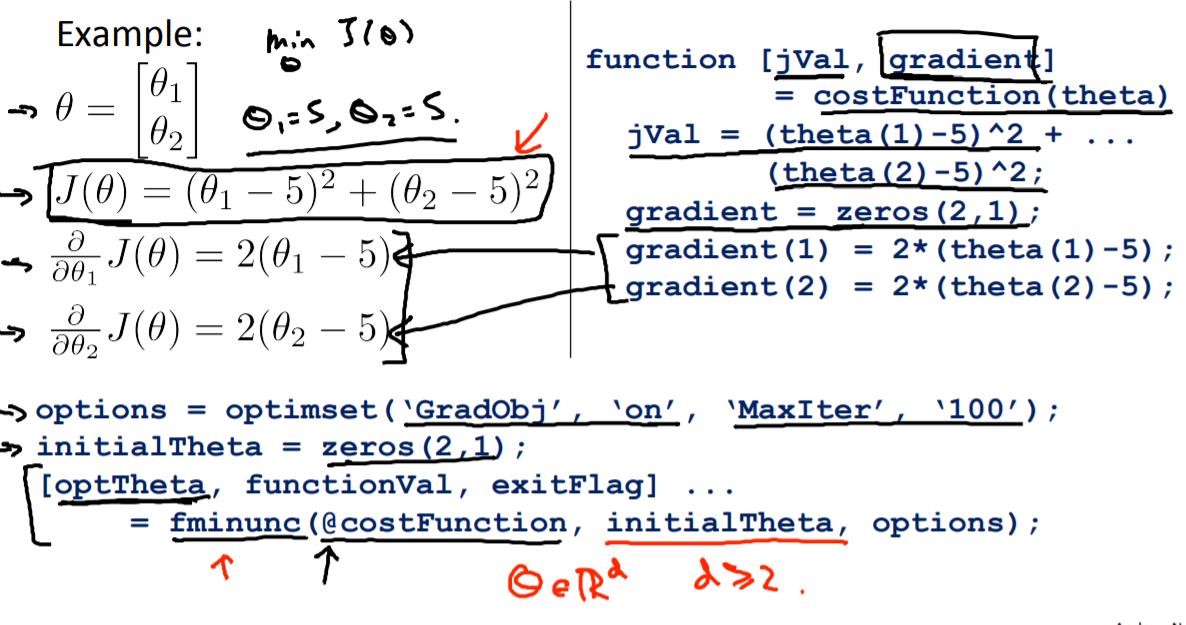
advanced optimization

对于高阶的优化方法，不介意自己实现，而是使用已经编写好的函数。

多分类问题

之前讨论的都是二分类，下面我们讨论多分类问题。

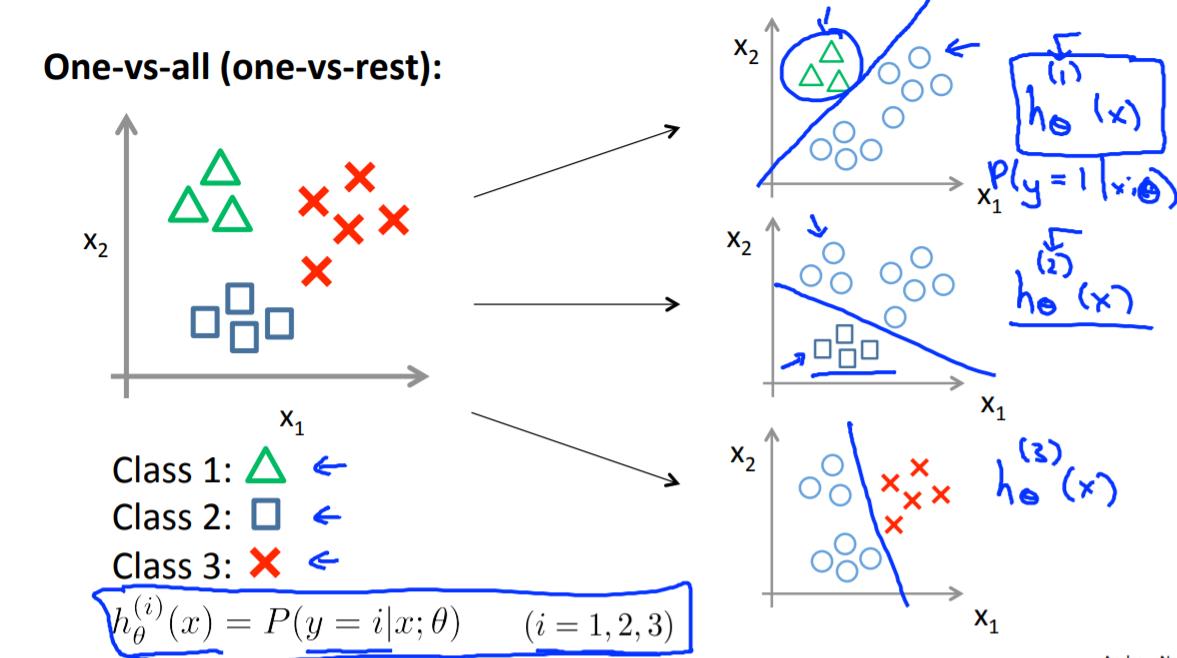
上述one-vs-all的主要思想是，每次将一类单拎出来，其他为另一类，这样就化为一个二分类问题，得到一个相应的$h_{\theta }(x{)}^i$ 函数，最终一共会得到n和预测函数，每一个预测函数代表着预测分类为i的概率。当有一个新的X需要分类时，分别计算出所有的$h_{\theta }^i$的值，取最大的那个，表示它为第i个分类的可能性最高，从而完成多分类任务。

matlab的实现思路：

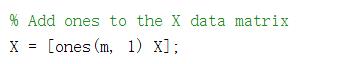
上面得到的 all_theta 每一行表示其中一类训练出来的对应的参数

得到的p矩阵即是最终的分类结果